Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (6 of 92) The Schrodinger Eqn. in 1-D (2/3)
TLDRThe video script delves into the quantum mechanics concepts of energy and momentum, particularly for photons and particles with mass. It explains the derivation of equations for the energy and momentum of a photon, and then transitions to discussing the energy of a massive particle, combining kinetic and potential energy. The script highlights the leap to equating the energy of a particle with the energy of a photon, leading to the development of the Schrödinger equation. The process of deducing this fundamental equation is described as a blend of educated guessing and the need for it to align with known wave-like behaviors of particles. The video sets the stage for further exploration in the subsequent episode, where the Schrödinger equation's solutions and their implications will be discussed.
Takeaways
- 🌟 The energy of a photon is described by the equation E = H bar * Omega, where Omega is the angular frequency.
- 🚀 The momentum of a photon is given by the equation P = H bar * K, with H bar being h / 2 pi and h being Planck's constant.
- 🔍 The energy of a massive particle is the sum of its kinetic and potential energy, with kinetic energy expressed as (1/2) * m * v^2 and potential energy represented by V.
- 🌊 Small particles exhibit wave-like properties similar to photons, leading to the substitution of energy and momentum in their respective equations.
- 📝 The guessed equation for the energy of a particle with mass is E = H bar * Omega = - (H bar^2 * k^2) / (2 * m) + V, which is only valid for particles with mass.
- 🤔 The process of deriving the energy equation involved educated guessing and multiple attempts, eventually leading to a correct description of a particle's wave.
- 🧠 The Schrödinger equation was initially guessed to have a similar form to the wave equation, but with modifications to account for the particle's potential energy.
- 📐 The guessed form of the Schrödinger equation is ∂ψ/∂t = (-H bar^2 / (2 * m)) * ∂^2ψ/∂x^2 + V * ψ, where ψ is the wave function.
- 🌈 The traditional wave solutions like sin(kx - Omega t) or cos(kx - Omega t) do not work with the new equation due to the first partial derivative term.
- 🔄 The approach to finding the differential equation was to work backwards from a guessed solution format to determine the equation's structure.
- 🔗 The constants in the equations are derived from the relationship between photons and small particles, reflecting the quantum nature of reality.
Q & A
What are the three equations discussed in the video?
-The three equations discussed are: 1) The energy of a photon, written as H bar times Omega (angular frequency), 2) The momentum of a photon, written as H bar times K, and 3) An equation describing the energy of a particle with mass, which is the sum of its kinetic and potential energy.
How is the energy of a photon related to its momentum and the speed of light?
-The energy of a photon is the product of its momentum and the speed of light (E = p * c).
What is the kinetic energy of a particle with mass?
-The kinetic energy of a particle with mass is given by the formula (1/2) * m * v^2, where m is the mass and v is the velocity of the particle.
How does the potential energy of a particle influence its total energy?
-The total energy of a particle with mass is the sum of its kinetic energy and its potential energy, represented by the symbol V.
What is the significance of the substitution of the energy in the equation with H bar Omega?
-The substitution of the energy in the equation with H bar Omega is a leap of faith based on the idea that small particles, like photons, exhibit wave-like properties, and this allows for the description of the wave-like behavior of particles such as electrons.
Why is the energy equation for a particle with mass only valid for real particles and not for photons?
-The energy equation for a particle with mass is only valid for real particles because photons, being massless, do not have potential energy in the same sense as particles with mass.
What is the Schrödinger equation mentioned in the script?
-The Schrödinger equation is a fundamental equation in quantum mechanics that describes how the quantum state of a physical system changes with time.
How did the scientists arrive at the form of the Schrödinger equation?
-The scientists used educated guessing and worked backwards from the known solutions of the wave equation to formulate the Schrödinger equation.
What is the role of the constant H bar in the equations?
-H bar, which is Planck's constant divided by 2 pi (h / 2 pi), is a fundamental constant that appears in the equations describing the energy and momentum of photons and the energy of particles with mass.
Why did the scientists replace the momentum P with H bar k in the energy equation?
-They replaced the momentum P with H bar k to incorporate the relationship between the momentum of a particle and its wave-like properties, as derived from the de Broglie hypothesis.
What is the significance of the wave function in the context of the Schrödinger equation?
-The wave function, which is a solution to the Schrödinger equation, provides information about the probability amplitude of finding a particle in a particular state or position.
How does the video script relate to the understanding of quantum mechanics?
-The script provides a foundational understanding of the mathematical constructs and principles that underpin quantum mechanics, such as the relationship between energy, momentum, and wave-like behavior of particles.
Outlines
🌟 Quantum Mechanics Foundations: Energy and Momentum of Photons
This paragraph introduces the basic concepts of quantum mechanics, focusing on the energy and momentum of photons. It explains that the energy of a photon is given by the product of Planck's constant (H bar) and the angular frequency (Omega), and the momentum is given by H bar times the wave number (K). The discussion then transitions to finding an equation for the energy of a particle with mass, which includes both kinetic and potential energy. The kinetic energy is expressed as 1/2 m v^2, and the potential energy is represented by V. The paragraph also describes how the energy and momentum of a photon are related to the energy and momentum of a particle, leading to the development of a new equation for the energy of a particle with mass.
📚 Deriving the Schrödinger Equation: The Quantum Leap
This paragraph delves into the process of deriving the Schrödinger equation, which describes the wave function of a particle. It starts by discussing the educated guesses and the iterative process that led to the development of the equation. The paragraph explains how the energy and momentum of a particle are substituted into the equation, leading to the famous Schrödinger equation in the form of h bar^2 k^2 / 2m plus V equals the product of Planck's constant and the second derivative of the wave function with respect to position, plus the potential energy times the wave function. It also touches on the limitations of the equation, noting that it is only valid for particles with mass and not for massless particles like photons. The paragraph concludes by hinting at the next steps, which involve exploring the solutions to the Schrödinger equation and understanding why certain solutions work while others do not.
Mindmap
Keywords
💡Photon
💡Energy
💡Momentum
💡Reduced Planck Constant (ħ)
💡Angular Frequency (Ω)
💡Potential Energy (V)
💡Kinetic Energy
💡Wave Equation
💡Schrödinger Equation
💡Quantum Mechanics
💡Wave-Particle Duality
Highlights
The video discusses the derivation of equations for the energy and momentum of a photon.
The energy of a photon is given by the equation E = H bar * Omega, where Omega is the angular frequency.
The momentum of a photon is described by the equation P = H bar * K, with H bar being h / 2 pi and H being Planck's constant.
The video then explores the energy of a particle with mass, which is the sum of its kinetic and potential energy.
The kinetic energy is expressed as (1/2) * m * v^2, and the potential energy is represented by the letter V.
A leap is made by substituting the energy in the kinetic energy equation with H bar Omega, based on the wave-like behavior of small particles.
The resulting equation for the energy of a particle with mass is H bar Omega = (p^2 / 2m) + V, where p is the momentum.
This equation is only valid for particles with mass, as photons do not have potential energy.
The video introduces the Schrödinger equation as a differential equation to describe particles in one dimension.
The Schrödinger equation is hypothesized to be a linear equation, solvable as the sum of two linear equations.
The first guess for the Schrödinger equation is derived from educated guessing and the known relationship between photons and small particles.
The video explains that the traditional wave equation solutions, such as sin(kx - Omega t), no longer apply to the new equation.
A new solution format is proposed that works with the Schrödinger equation, which will be explored in the next video.
The process of deriving the Schrödinger equation is based on working backwards from a desired solution format.
The constants in the Schrödinger equation are derived from the relationship between photons and small particles.
The video sets the stage for the next installment, where the derivation and validation of the Schrödinger equation will be further explored.
Transcripts
Browse More Related Video
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (5 of 92) The Schrodinger Eqn. in 1-D (1/3)
How Schrodinger Came Up With His Famous Equation (But EASIER)
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (15 of 92) Time & Position Dependencies Ex.*
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (4 of 92) The Schrodinger Eqn. "Derived"
Special Relativity | Lecture 3
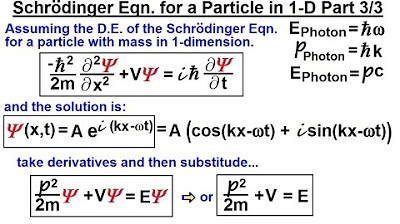
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (7 of 92) The Schrodinger Eqn. in 1-D (3/3)
5.0 / 5 (0 votes)
Thanks for rating: