Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (5 of 92) The Schrodinger Eqn. in 1-D (1/3)

Michel van Biezen
28 Jan 201705:23
EducationalLearning
32 Likes 10 Comments

TLDRThe video script delves into the development of the Schrödinger equation for a particle in one dimension by drawing parallels between the wave-like behavior of small particles and photons. It begins with the general wave equation, exploring the relationship between the electric field, position, and time. The script then transitions to the energy and momentum of photons, using Planck's constant and the speed of light to derive equations. The goal is to establish a framework that links the energy of a photon to its momentum and frequency, ultimately aiming to apply these concepts to derive the Schrödinger equation in the context of single-particle quantum mechanics.

Takeaways
  • 🌟 The goal is to develop the Schrödinger equation for a particle in one dimension by drawing parallels between small particles and photons, both exhibiting wave-like behavior.
  • 📐 The general wave equation in one dimension is introduced, relating the second derivative of the electric field with respect to position and time.
  • 🌊 The electric field solution is expressed as a sinusoidal wave, with maximum electric field displacement, angular frequency, wave number, and speed of light playing key roles.
  • 🔄 By differentiating the wave equation with respect to time and position, relationships between the angular frequency (Ω) and wave number (K) are established.
  • 💡 The energy of a photon is related to its frequency through Planck's constant, leading to the expression of energy in terms of angular frequency (h-bar times Ω).
  • 🚀 The momentum of a photon is derived as h-bar times the wave number (K), eliminating mass considerations for massless particles like photons.
  • 🌐 The energy-momentum relationship for photons is expressed as momentum times the speed of light, simplifying to E=pc without mass considerations.
  • 🔢 Three key equations are derived from the analysis: the energy of a photon in terms of frequency (hΩ), the momentum of a photon (h-bar K), and the energy-momentum relationship (E=pc).
  • 📚 The derived equations will be used in part two to further develop the Schrödinger equation for a single particle in one dimension.
  • 🎯 The process highlights the importance of understanding wave-particle duality and the mathematical framework that connects the properties of photons to the behavior of particles in quantum mechanics.
Q & A

  • What is the main goal of the script?

    -The main goal of the script is to develop the Schrödinger equation for a particle in one dimension by drawing parallels between small particles and photons, which both exhibit wave-like behavior.

  • How does the script begin to establish the relationship between particles and waves?

    -The script begins by comparing the behavior of small particles to small photons, noting that both act like waves, suggesting a fundamental similarity between them.

  • What is the general wave equation mentioned in the script?

    -The general wave equation mentioned is ∂²E/∂x² = 1/c² ∂²E/∂t², where E represents the electric field, c is the speed of light, and the partial derivatives are with respect to position and time.

  • How is the electric field represented as a function of position and time in the script?

    -The electric field is represented as a simple wave equation: E = A * cos(kx - ωt), where A is the maximum electric field displacement, k is the wave number (2π/λ), ω is the angular frequency (2πf), and c is the speed of light.

  • What is the relationship between wave number (k) and angular frequency (ω) derived from the script?

    -The relationship derived is k = ω/c, which can also be rearranged to ω = k * c or ω = 2πf, indicating that the angular frequency is directly proportional to the wave number times the speed of light.

  • How is the energy of a photon expressed in terms of Planck's constant and frequency?

    -The energy of a photon is expressed as E = h * f, where h is Planck's constant and f is the frequency. Since frequency f is ω/2π, this can also be written as E = h * (ω/2π) or E = ħ * ω, with ħ being Planck's constant divided by 2π (h-bar).

  • What is the relationship between the momentum of a photon and its energy?

    -The momentum of a photon is related to its energy by the equation p = E/c, where p is the momentum, E is the energy, and c is the speed of light.

  • How can the momentum of a photon be expressed in terms of Planck's constant?

    -The momentum of a photon can be expressed as p = ħ * k, where ħ is Planck's constant divided by 2π (h-bar) and k is the wave number (2π/λ).

  • What are the three key equations derived from the script that will be carried over to part two?

    -The three key equations are: (1) The energy of a photon is h * f (or ħ * ω), (2) The momentum of a photon is ħ * k, and (3) The energy of a photon can also be expressed as p * c.

  • How does the script connect the energy, momentum, and frequency of a photon?

    -The script connects these concepts by showing that the energy (E) of a photon is proportional to its frequency (f), the momentum (p) is proportional to the wave number (k), and the energy can also be expressed as the product of momentum and the speed of light (p * c).

  • What is the significance of the wave equation and the derived relationships in understanding the behavior of particles and photons?

    -The wave equation and the derived relationships are significant because they provide a mathematical framework for understanding the dual wave-particle nature of light and matter, as described by quantum mechanics. They help establish the fundamental principles that lead to the development of the Schrödinger equation for particles in one dimension.

Outlines
00:00
🌟 Introduction to the Schrodinger Equation and Wave-Particle Duality

The paragraph introduces the process of developing the Schrodinger equation for a particle in one dimension by drawing parallels between small particles that exhibit wave-like behavior and small photons. It explains that the general wave equation in one dimension is used as a starting point, leading to the electric field being described as a simple wave. The paragraph then delves into the mathematical derivations involving second derivatives with respect to time and position, resulting in the relationship between angular frequency (Omega) and wave number (K). It further connects this to the energy of photons, expressed in terms of Planck's constant and frequency, and eventually to the momentum of a photon, derived from the relationship between energy and momentum. The paragraph concludes with three key equations that will be used in the next part of the derivation.

05:00
📝 Derivation of Photon Properties and Setup for Part Two

This paragraph continues the discussion from the previous one, focusing on the energy and momentum of photons and how they can be expressed in terms of frequency and the constants associated with quantum mechanics. It reiterates the three key equations derived earlier: the energy of a photon in terms of frequency (or angular frequency), the momentum of a photon, and the energy-momentum relationship. The paragraph emphasizes the importance of these equations as a foundation for the subsequent derivation of the Schrodinger equation for a single particle in one dimension, setting the stage for part two of the explanation.

Mindmap
Keywords
💡Schrodinger Equation
The Schrodinger Equation is a fundamental equation in quantum mechanics that describes how the quantum state of a physical system changes with time. In the context of this video, the goal is to develop the Schrodinger Equation for a particle in one dimension, which is a key step in understanding quantum behavior. The script outlines a process that begins with the general wave equation and eventually leads to the formulation of the Schrodinger Equation by drawing parallels between particles and waves.
💡One Dimension
One dimension refers to the simplification of a physical system to a single spatial axis for the purpose of mathematical modeling and analysis. In the video, the focus is on developing the Schrodinger Equation for a particle that is confined to movement along a single line, which simplifies the complex three-dimensional reality into a more manageable one-dimensional model.
💡Wave Equation
The wave equation is a mathematical model that describes the behavior of waves, including their propagation through space and time. In the video, the wave equation is used as a starting point to derive the Schrodinger Equation, with the electric field being represented as a wave that varies with position and time.
💡Electric Field
The electric field is a region around a charged particle where an electric force is exerted on other charged particles. In the context of the video, the electric field is used to represent the wave-like behavior of photons, which are particles that also exhibit wave properties. The script describes the electric field in terms of its maximum value, frequency, wavelength, and how it varies with position and time.
💡Angular Frequency
Angular frequency, denoted by Omega, is a measure of how quickly a wave oscillates, defined as the rate of change of the angle per unit time. It is related to the frequency (F) by the equation Omega equals 2 pi times the frequency. In the video, angular frequency is used to describe the oscillation of the electric field in the wave equation and is crucial in the derivation of the Schrodinger Equation.
💡Wave Number
The wave number, symbolized by K, is a measure of the spatial frequency of a wave, defined as the number of oscillations or waves per unit length. It is inversely related to the wavelength (lambda), calculated as 2 pi divided by the wavelength. In the video, the wave number is used to describe the periodic nature of the electric field in the wave equation and plays a role in the development of the Schrodinger Equation.
💡Speed of Light
The speed of light, denoted by C, is the ultimate speed at which all conventional matter and information in the universe can travel. It is a fundamental constant in physics and is used in the video to relate the energy and momentum of photons to their frequency and wavelength. The script also uses the speed of light to derive relationships between the wave number and angular frequency.
💡Energy
In the context of the video, energy refers to the property of a system that is associated with the ability to do work. For photons, which are massless particles, their energy is related to their frequency through Planck's constant. The script discusses how the energy of a photon can be expressed in terms of its frequency and momentum, which is crucial for understanding the quantum behavior of particles.
💡Momentum
Momentum is a measure of the quantity of motion of an object, defined as the product of its mass and velocity. In the context of the video, momentum is used to describe the motion of photons, which are massless particles. The script relates the momentum of a photon to its energy and wave properties, using the equation where momentum equals the product of the energy and the speed of light divided by the angular frequency.
💡Planck's Constant
Planck's constant is a fundamental constant in quantum mechanics that relates the energy of a photon to its frequency. It is denoted by 'h' and is used in the video to express the energy of photons in terms of their frequency, as well as to relate the momentum of a photon to its wave number through the equation involving h-bar times K.
💡Photon
A photon is a massless, elementary particle that carries electromagnetic energy, exhibiting both wave-like and particle-like properties. In the video, photons are used as an example to illustrate the wave-particle duality and to derive relationships between energy, momentum, and wave properties that are essential for the development of the Schrodinger Equation.
Highlights

Developing the Schrödinger equation for a particle in one dimension.

Comparing small particles that act like waves to small photons.

Starting with the general wave equation in one dimension for the electric field.

The solution to the wave equation is assumed to be a simple wave function.

Deriving the second derivative of the electric field with respect to time and position.

Elimination of the electric field function leads to the equation K equals Omega over C.

Energy of a photon is expressed as Planck's constant times the frequency.

Momentum of a photon is derived as h-bar times K.

Energy of a photon can also be expressed as momentum times the speed of light.

For a photon, energy is simply equal to momentum times C since it has no mass.

Three key equations derived from the analysis: energy as a function of frequency, momentum as h-bar times K, and energy as momentum times C.

Objective is to develop a Schrödinger equation for a single particle in one dimension.

The general wave equation applies to electromagnetic radiation and the electric field.

The solution allows for the formulation of the energy and momentum of a photon in different forms.

Continuing to derive the Schrödinger equation for a particle in one dimension in part two.

The derivation process establishes a connection between wave-like particles and photons.

The theoretical framework has practical applications in quantum mechanics.

Transcripts

Browse More Related Video

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (6 of 92) The Schrodinger Eqn. in 1-D (2/3)

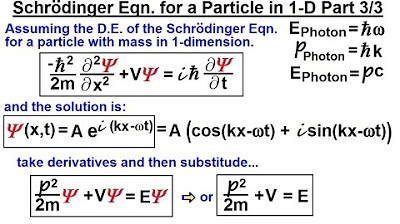
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (7 of 92) The Schrodinger Eqn. in 1-D (3/3)

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (15 of 92) Time & Position Dependencies Ex.*

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (19 of 92) Particle in 1-D Box: Example 1/2

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (12 of 92) Time & Position Dependencies 1/3

24. Quantum Mechanics VI: Time-dependent Schrödinger Equation

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
QuantumMechanicsSchrodingerEquationWaveParticleDualityElectromagnetismPhotonsMathematicalDerivationPhysicsEducationQuantumTheoryWaveEquation