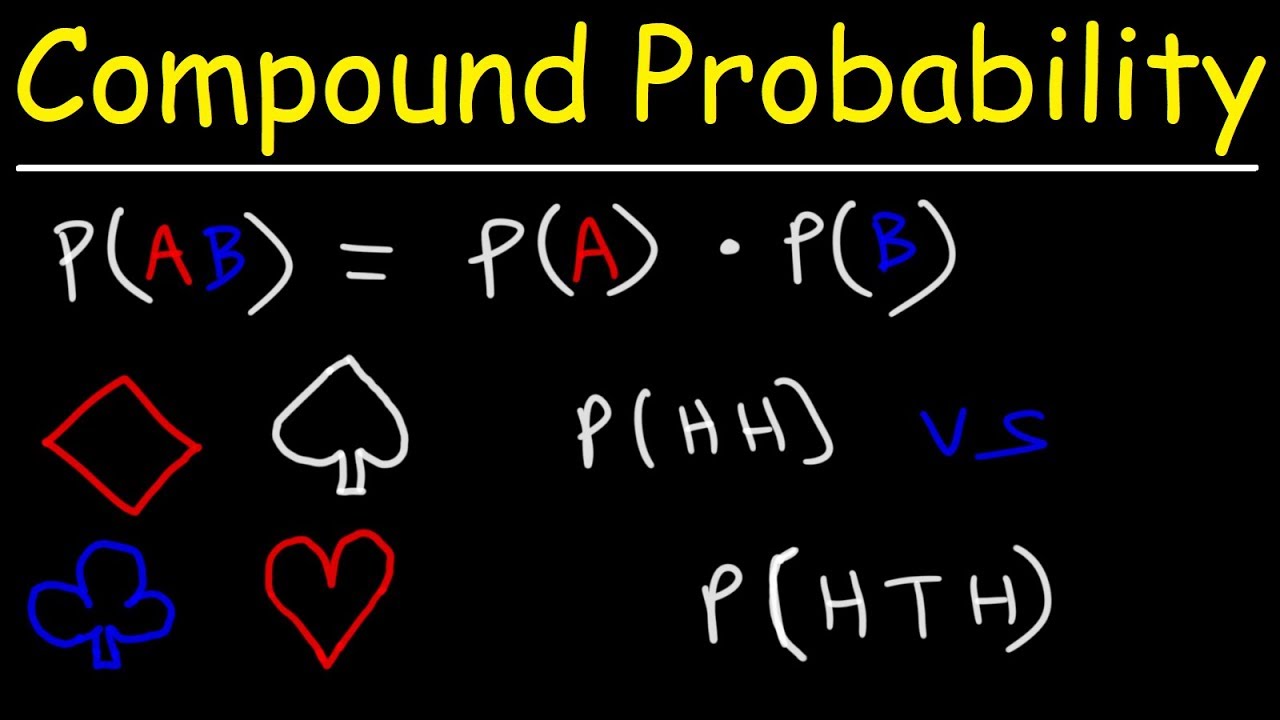
Probability Tree Diagrams

The Organic Chemistry Tutor

14 Nov 201832:52

EducationalLearning

32 Likes 10 Comments

TLDRThis video explains how to use tree diagrams to solve probability problems. It provides step-by-step examples of creating tree diagrams to represent different scenarios, calculate individual and compound event probabilities, handle problems with and without replacement, independent and dependent events, and apply formulas like P(A or B) = P(A) + P(B) and P(A) = 1 - P(not A). Viewers learn how tree diagrams help organize outcomes and probabilities to tackle multi-step probability questions through several examples including selecting marbles from bags, neighborhood car sampling, and more.

Takeaways

😀 Tree diagrams are useful for visualizing all the possible outcomes for probability problems
👍 For dependent events, subsequent probabilities change based on prior selections
📏 Calculate probability by dividing the number of favorable outcomes by total possible outcomes
🔢 Use AND to multiply probabilities, OR to add probabilities
💡 The probability of at least one outcome is 1 minus the probability of its complement
🎯 Be clear whether order of outcomes matters or not
🌳 You can calculate total possible outcomes from tree diagram branches
✅ Probabilities on each branch level should sum to 1
🖊 Percents and decimals can help calculate part of a whole
📈 Using percentages at each branch enables back-calculating totals

Q & A

What is a tree diagram and how is it used to solve probability problems?
-A tree diagram is a graphical representation used to analyze all the possible outcomes of an event. It starts with the initial possibilities and branches out to show all potential outcomes. Tree diagrams help visualize probability problems and make it easier to calculate the probabilities.
What does 'with replacement' mean when selecting multiple items from a population?
-'With replacement' means that after an item is selected, it is placed back into the population before the next selection. So the total population size stays the same for each selection.
What is the difference between dependent and independent events in probability?
-Independent events mean that the outcome of one event does not affect the outcome of another event. Dependent events mean that the outcome of the second event depends on what happened in the first event.
When calculating probability, why do you multiply probabilities for 'and' events but add probabilities for 'or' events?
-For an 'and' statement, you need both events to happen, so you multiply the probabilities. For an 'or' statement, you just need one or the other to happen, so you add the probabilities.
What does it mean when a question asks for the probability of selecting 'at least' one option?
-When asked for the probability of 'at least' one option, it includes getting that option once or multiple times. You calculate this probability by adding up the probabilities of all outcomes with 1 or more of that option.
What is the difference between 'with replacement' and 'without replacement'?
-'With replacement' means putting back each item before selecting again so population size stays the same. 'Without replacement' means the population size reduces by 1 after each selection.
Why does the total of all probabilities on a tree diagram add up to 1?
-Because a probability represents the chance of something happening. Taken together, all possible outcomes must add up to 100% chance or 1.
How do you calculate the total number of outcomes with multiple successive selections?
-Multiply the number of options at each selection stage. E.g. choosing Red or Blue then Red or Blue again is 2x2=4 total possible outcomes.
What information is given in the example with cars of different colors and types?
-The total cars, percentage black vs white cars, percentage sedan vs SUV for each color, which provides the count of each subgroup needed to solve the probability questions.
What are the two ways shown to calculate the probability of selecting a black sedan?
-1) Count black sedans and divide by total cars. 2) Multiply % black cars and % black cars that are sedans.

Outlines

00:00

📊 Using tree diagrams to calculate probability

This paragraph explains how to use a tree diagram to calculate the probability of selecting two blue marbles from a bag with 8 red and 12 blue marbles. It walks through constructing the tree diagram to represent all possible outcomes and calculating the probabilities along each branch.

05:01

🤔 Calculating 'at least one' probability

This paragraph continues the marble probability example, explaining how to calculate the probability of selecting at least one red marble. It shows two methods: 1) adding the probabilities of outcomes with at least one red or 2) using the formula P(at least one red) = 1 - P(no reds).

10:02

❗️ Concept of 'without replacement'

This paragraph introduces a new marble probability example involving drawing marbles without replacement. It explains how this changes the probabilities on each draw, since the contents of the bag change after each pick. A tree diagram is constructed to represent this.

15:03

🤝 Expanding to three selections

This paragraph builds on the previous marble probability example by having the person select three marbles instead of two. It walks through expanding the tree diagram for three selections and eight possible outcomes. It then calculates the probability of selecting at least one red marble.

20:06

😅 Calculating 'at most two' blue marbles

Continuing the three marble selection example, this calculates the probability of selecting at most two blue marbles. It explains this is equal to the probability of not selecting three blue marbles. The concepts of 'at least' and 'at most' probabilities are compared.

25:07

🚘 Probability example with cars

This paragraph introduces a more complex, real-world probability example involving different types of cars in a neighborhood. A tree diagram splits up the cars by color and type. It then calculates the probability of selecting a black sedan at random.

30:09

💡 Using percentages to calculate probability

Continuing the car example, this shows an alternative way to calculate probabilities using percentages at each branch of the tree diagram. It also answers how many white SUVs are in the neighborhood.

Mindmap

Keywords

💡probability

The video focuses on using tree diagrams to calculate the likelihood of certain events happening. Probability refers to the chance that a particular event will occur. The script provides examples of calculating probability based on the numbers of certain colored marbles in bags.

💡tree diagram

A tree diagram is a graphical tool used to analyze different possible outcomes and calculate their probabilities. The script shows how to map out different possible marble selections on tree branches to denote all outcomes.

💡replacement

Replacement refers to putting a marble back into the bag after selecting it. This means each selection is an independent event with the same probability every time. The script contrasts this with no replacement where probabilities change.

💡dependent events

Dependent events are those where the probability of one event relies on or is influenced by previous events. When marbles are selected without replacement, the probabilities change based on prior selections.

💡at least

Questions like "at least one red marble" involve summing the probabilities of outcomes with one or more red marbles. The script shows how this relates to the inverse probability of selecting all blue marbles.

💡exactly

Asking for the probability of exactly a certain number of blue marbles means only counting cases with that exact number, not more or less. The script illustrates this in a 3-marble problem.

💡at most

At most 2 blue marbles means 2 blue marbles or any lower number. So you include probabilities of 0, 1, and 2 blue marbles. The script relates this to the inverse of getting 3 blue marbles.

💡multiply

When events are connected with "and", their probabilities must be multiplied. The script shows examples like a red then blue marble.

💡add

When alternative events are described with "or", their probabilities are added. The script adds probabilities for different cases of red and blue marbles.

💡percentage

Many probability calculations end up as decimals, which can be converted into percentages by multiplying by 100. The script shows examples of reporting both decimal and percentage values.

Highlights

Use tree diagrams to visually represent all possible outcomes and calculate probabilities

"And" indicates multiplying probabilities, "or" indicates adding probabilities

With replacement means putting the marble back so probabilities stay the same

The probability of at least one event equals 1 minus the probability of its opposite

Without replacement changes the probabilities for subsequent selections

Dependent events have probabilities that rely on previous events

Independent events have stand-alone probabilities unaffected by other events

Order matters when calculating the specific sequence probability vs. any order

Calculate total outcomes as the number of options raised to the selections power

Use percentages of total and tree diagrams to break down subgroup probabilities

Multiply percentages along branches of tree diagram to get probabilities

Visualizing all possible outcomes helps answer complex probability questions

"At most" means the maximum allowed number, including lower amounts

"Exactly" means only that specific number is allowed, no more or less

Using tree diagrams and percentages can solve complex real-world probability problems

Transcripts

Browse More Related Video

4.2.2 Addition and Multiplication Rules - The Addition Rule

Math 119 Chapter 4 part 2

Probability of Complementary Events & Sample Space

Compound Probability of Independent Events - Coins & 52 Playing Cards

Chapter 4 Probability Part 1

Probability of Mutually Exclusive Events With Venn Diagrams