Continuous Probability Distributions - Basic Introduction

The Organic Chemistry Tutor
16 Sept 201910:12
EducationalLearning
32 Likes 10 Comments

TLDRThe transcript describes various continuous probability distributions, such as the normal distribution. It defines f(x), the probability density function, and explains how to calculate probabilities and areas under the curve for continuous distributions. Formulas are provided for the uniform distribution and the exponential distribution. Key points discussed include: the total area under any continuous distribution curve equals 1, the probability of X equaling any single value is 0, the heights and shapes of different distributions like normal and uniform, and how to calculate areas under curves to determine probabilities.

Takeaways
  • 😀 The normal distribution is a continuous probability distribution where the random variable X can take on any value.
  • 📈 The probability density function f(X) gives the height of the curve above the x-axis at a given X value.
  • �integrl The total area under a continuous probability distribution curve is always 1.
  • 📏 To calculate probability for a range, find the area under the curve for that range.
  • 👉 The probability that X equals a single value is 0 as there is no area.
  • 📊 Other continuous probability distributions include the uniform and exponential distributions.
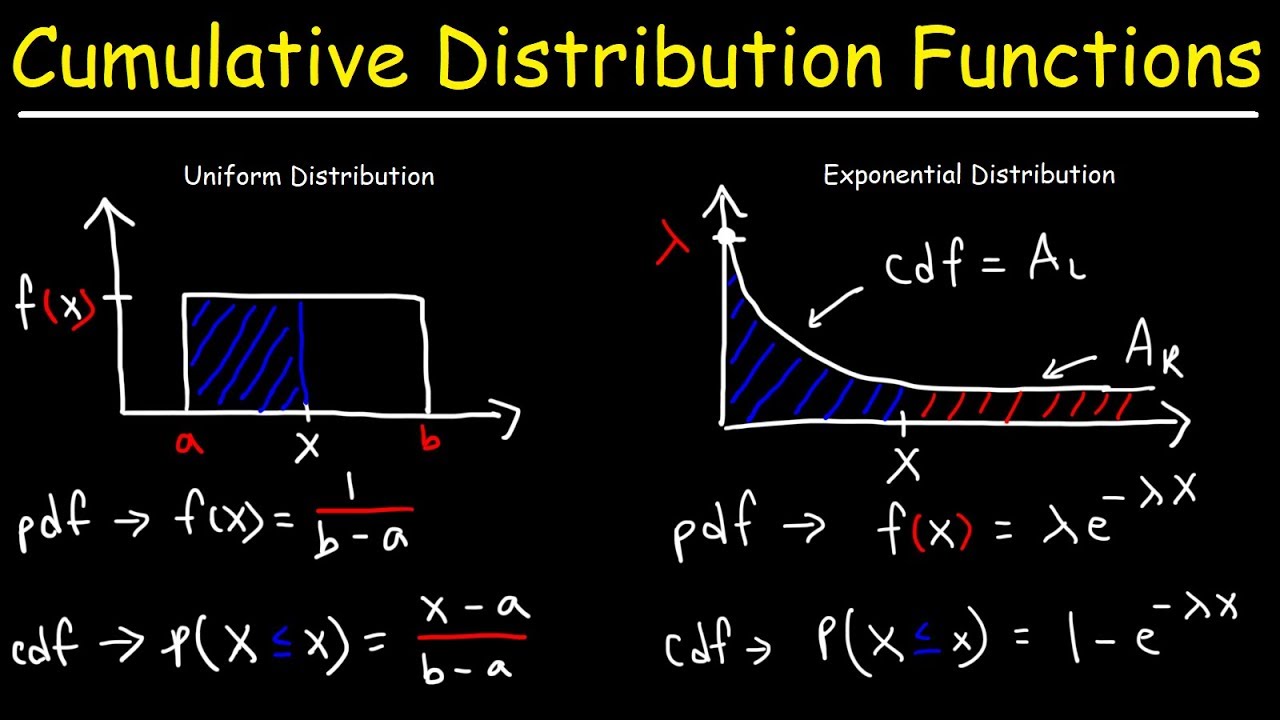
  • 🔢 For a uniform distribution, f(X) is constant and the area is 1.
  • 🎯 The mean of a uniform distribution is the average of the endpoints.
  • ⚖️ The exponential distribution has a decreasing curve with intercept λ.
  • 🏁 Key formulas help calculate probabilities under the exponential distribution curve.
Q & A

  • What does the probability density function (PDF) represent on a continuous probability distribution?

    -The probability density function f(X) represents the height of the curve above the x-axis at some point X. It gives the distance between the curve and the x-axis at that point.

  • Why is the total area under a continuous probability distribution curve always equal to 1?

    -The total area under a continuous probability distribution curve represents all possible values that the random variable X can take. Since X must take some value, the total area sums to 1, representing probability 1 or 100%.

  • What is the probability that the continuous random variable X takes on a single exact value?

    -The probability that X takes on a single exact value is 0. At a single point, the area under the curve is 0 because there is height but no width. To have non-zero probability, X needs a range of values.

  • How do you calculate probability for a continuous distribution?

    -To calculate probability, you need to calculate the area under the curve over the range of X values of interest. For example, to calculate P(X < a), you calculate the area under the curve to the left of point a.

  • What is the key characteristic of a uniform distribution?

    -A uniform distribution has a constant f(X) value over the range from A to B. This makes the distribution shaped like a rectangle with area 1.

  • How do you calculate the probability density function f(X) for a uniform distribution?

    -For a uniform distribution from A to B, f(X) = 1 / (B - A). This makes the area of the rectangle 1.

  • What is the exponential distribution and what does it represent?

    -The exponential distribution is a continuous distribution used to model time between random events, such as radioactive decay. It has a decreasing curve over time. The rate parameter λ represents the frequency of events.

  • How do you calculate probability for an exponential distribution?

    -To calculate P(X < x) for exponential, the formula is 1 - e^(-λx). For P(X > x), the formula is simply e^(-λx).

  • What is the relationship between the rate parameter λ and the mean for an exponential distribution?

    -For an exponential distribution, λ = 1/mean. So if you know the mean time between events, you can calculate λ, which defines the distribution.

  • What are some other continuous probability distributions that are important to know?

    -Other important continuous probability distributions are the normal/Gaussian distribution, gamma distribution, chi-squared distribution, Student's t-distribution, and more. These come up often in statistics and probability.

Outlines
00:00
😀 Defining Continuous Probability Distributions

This paragraph defines continuous probability distributions, where the random variable X can take on any value along the x-axis. It explains key properties like the probability density function f(X), calculates probability as the area under the curve, and how a point has 0 area. It also discusses rules for probability calculations like P(X < a) = P(X ≤ a).

05:01
😊 Overview of Uniform and Exponential Distributions

This paragraph provides an overview and key formulas for the uniform distribution, where f(X) is constant between two endpoints. It also introduces the exponential distribution, defines properties like the rate parameter lambda, and shows how to calculate probability less than or greater than a value of X.

10:03
😃 Calculating Probability for Exponential Distribution

This final paragraph shows formulas for calculating the probability that X is less than or greater than a value X for the exponential distribution. It emphasizes that the total area under any continuous probability distribution curve is 1.

Mindmap
Keywords
💡continuous probability distribution
A probability distribution defined over a continuous sample space, as opposed to a discrete one. The video focuses on continuous probability distributions like the normal and uniform distributions. The area under the curve represents probabilities.
💡normal distribution
A continuous probability distribution that is symmetric and centered around the mean. It is one of the examples of a continuous distribution discussed in the video.
💡probability density function (PDF)
A function that describes the relative likelihood of a random variable taking on a given value. Denoted as f(X). The height of the PDF corresponds to this relative likelihood.
💡area under the curve
The area under a continuous probability distribution, which corresponds to probabilities. The video emphasizes that this area sums to 1.
💡uniform distribution
A continuous distribution with constant probability density between two bounds. One example discussed in the video.
💡exponential distribution
Another continuous probability distribution example covered in the video. Defined by a rate parameter lambda.
💡mean
A measure of central tendency. For a uniform distribution, it is the average of the lower and upper bounds.
💡standard deviation
A measure of spread or variance around the mean. Provided for the uniform distribution.
💡lambda
The rate parameter that defines an exponential distribution. Equal to the inverse of the mean.
💡y-intercept
Where a curve meets the y-axis. Shown in the context of an exponential distribution.
Highlights

A continuous probability distribution has a continuous random variable X that can take any value

The probability density function f(X) gives the height of the curve above the x-axis at a point X

The total area under the curve for a continuous probability distribution is always equal to 1

To calculate probability for a range, you calculate the area under the curve for that range

f(X) is always greater than or equal to 0 for a continuous probability distribution

The probability of X equaling any single value is 0 because there is no width to calculate area

Uniform distribution has constant f(X) value over a range from A to B with total area = 1

For uniform distribution, f(X) = 1/(B - A)

Exponential distribution decreases over time/X with y-intercept = lambda

Lambda = 1/mean for exponential distribution probability density function

Total area under any continuous probability distribution curve = 1

P(X < X) for exponential = 1 - e^(-lambda*X)

P(X > X) for exponential = e^(-lambda*X)

Mean for uniform distribution = (A + B)/2

Standard deviation for uniform = (B - A)/sqrt(12)

Transcripts

Browse More Related Video

Cumulative Distribution Functions and Probability Density Functions

6.1.2 The Standard Normal Distribution - Uniform Distributions

6.1.0 The Standard Normal Distribution - Lesson Overview, Learning Outcomes

6.2.1 Nonstandard Normal Distributions -Converting B/t Standard and Nonstandard Normal Distributions

Continuous Random Variables: Probability Density Functions

Elementary Stats Lesson #11

Rate This

5.0 / 5 (0 votes)

Thanks for rating: