Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (15 of 92) Time & Position Dependencies Ex.*

Michel van Biezen
11 Feb 201706:09
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses solving the time-independent Schrödinger equation for a particle moving in one dimension with zero potential energy. It outlines the process of taking the first and second derivatives of the wave function with respect to position, and substituting these into the equation to verify its validity. The explanation culminates in demonstrating that the total energy of the particle, represented by the kinetic energy, matches the left side of the equation, confirming the wave function's correctness. The video also makes an analogy to the momentum of a photon, equating it to the particle's momentum (p=ħk), thereby validating the wave function for the given scenario.

Takeaways
  • 📝 The script discusses solving the time-independent Schrödinger equation for a particle moving in one dimension with zero potential energy.
  • 🌊 The wave function given is position-dependent, simplifying the equation as the potential energy term becomes zero.
  • 🔄 The process involves finding the first and second derivatives of the wave function with respect to position (X).
  • 📈 The first derivative involves the trigonometric functions sine and cosine, with a factor of K (the wave number).
  • 📊 The second derivative calculation results in an expression that matches the original wave function, confirming the equation's validity.
  • 🎯 The substitution of the second derivative into the Schrödinger equation verifies that the left side equals the right side, confirming the wave function's correctness.
  • 🌐 The total energy of the particle is considered to be purely kinetic since the potential energy is zero.
  • 💫 The kinetic energy is expressed as the square of the momentum divided by twice the mass (p²/2m).
  • 📌 The momentum of a photon is equivalent to ħK (h-bar times K), which is used to express the particle's momentum in this context.
  • 🔗 The script concludes by showing that the left side of the equation, involving h-bar squared times K squared divided by 2m, equals the right side, confirming the wave function's validity.
  • 🎓 The process exemplifies a method for solving and verifying wave functions in the context of quantum mechanics.
Q & A

  • What is the format of the equation discussed at the beginning of the transcript?

    -The format discussed at the beginning is a time-independent equation.

  • What is the significance of the potential energy being equal to zero in this context?

    -When the potential energy is equal to zero, it simplifies the equation as the term involving potential energy becomes zero, making the analysis easier.

  • What is the first derivative of the wave function with respect to position X?

    -The first derivative of the wave function with respect to X is K*a*cos(K*X) - K*b*sin(K*X), where K is the wave number, a and b are coefficients of the wave function.

  • How is the second derivative of the wave function derived?

    -The second derivative is derived by taking the derivative of the first derivative, which results in -K^2*a*sin(K*X) + K^2*b*cos(K*X).

  • What does the speaker do after obtaining the second derivative of the wave function?

    -After obtaining the second derivative, the speaker substitutes it into the time-independent Schrödinger equation to verify if the left side equals the right side, which it does, confirming the validity of the wave function.

  • What is the relationship between the total energy of the particle and the kinetic energy in this scenario?

    -Since the potential energy is zero, the total energy of the particle is equal to its kinetic energy.

  • How is the kinetic energy expressed in terms of the momentum of a particle?

    -The kinetic energy is expressed as the square of the momentum divided by 2m, where m is the mass of the particle.

  • What does the speaker conclude about the wave function after the analysis?

    -The speaker concludes that the wave function is proper for the time-independent Schrödinger equation for a particle moving in one dimension with zero potential energy.

  • What is the significance of the momentum of a photon in the context of this problem?

    -The momentum of a photon, which is H bar times K, is used to replace the momentum of the particle in the equation, showing that the wave function satisfies the time-independent Schrödinger equation.

  • How does the speaker correct a mistake in the equation during the analysis?

    -The speaker corrects the mistake by changing H bar to H bar squared in the equation, which aligns with the correct form of the time-independent Schrödinger equation.

  • What is the final confirmation of the wave function's validity?

    -The final confirmation is that the left side of the equation, which includes H bar squared times K squared divided by 2m times the wave function, is equal to the right side, which represents the energy times the wave function, thus proving the wave function's validity.

Outlines
00:00
📚 Solving the Time-Independent Wave Equation

This paragraph delves into the process of solving a time-independent wave equation for a particle with mass M moving in one dimension under zero potential energy. The speaker begins by explaining the need to find the second derivative of a given wave function with respect to position X. The first derivative is derived from the sine function, resulting in K times the cosine of KX. The second derivative calculation involves the negative sine and cosine functions, leading to a function that matches the original wave function, confirming the validity of the equation. The speaker then attempts to substitute the second derivative into the Schrödinger equation, correcting a mistake by replacing H bar with H bar squared. The equation is ultimately balanced by equating the kinetic energy to the total energy of the particle, given that the potential energy is zero. The energy expression is then related to the momentum of a particle, leading to the conclusion that the wave function satisfies the time-independent Schrödinger equation for the given conditions.

05:01
🌟 Relating Particle Momentum to Photon Momentum

In this paragraph, the speaker connects the momentum of a photon, represented as H bar times K, to the momentum of the particle in question. By replacing the particle's momentum with the photon's momentum in the wave function, the left side of the equation becomes equal to the right side, demonstrating that the wave function is indeed a proper solution for the time-independent Schrödinger equation. This substitution shows that the wave function accurately describes a particle moving in one dimension under the specified conditions, confirming the correctness of the approach and providing a clear understanding of how the wave function relates to the momentum of a photon.

Mindmap
Keywords
💡Time Independent Equation
A time independent equation is a mathematical representation that does not change over time, meaning it does not involve time as a variable. In the context of the video, this refers to the specific form of the Schrödinger equation being discussed, which describes the quantum state of a system where the potential energy is constant or zero. This simplifies the equation and allows for easier analysis of the system's behavior.
💡Wave Function
In quantum mechanics, the wave function is a mathematical description of the quantum state of a system. It provides information about the probability of finding a particle in a particular state or position. The wave function is central to understanding quantum behavior and is used to calculate various physical properties of particles. In the video, the wave function is said to depend only on position, simplifying the problem to a one-dimensional scenario.
💡Second Derivative
The second derivative of a function is the derivative of its first derivative. It measures how the rate of change of the function is changing. In the context of the video, finding the second derivative of the wave function with respect to position (X) is a crucial step in solving the time independent Schrödinger equation. This derivative helps determine the energy of the particle in the quantum system.
💡Potential Energy
Potential energy is the stored energy of a system, which has the potential to be converted into kinetic energy. It is dependent on the position of objects relative to each other and other factors. In the video, the potential energy is set to zero, simplifying the Schrödinger equation and indicating that there are no external forces doing work on the system.
💡Schrödinger Equation
The Schrödinger equation is a fundamental equation in quantum mechanics that describes how the quantum state of a physical system changes with time. It is a partial differential equation that is central to understanding quantum behavior. The time-independent version of this equation is used when the system is in a steady state and does not change over time.
💡Kinetic Energy
Kinetic energy is the energy of motion possessed by an object. It is defined as one half of the product of the object's mass and the square of its velocity. In the context of the video, since potential energy is zero, the total energy of the particle is equivalent to its kinetic energy. This concept is used to relate the wave function to the energy of the particle.
💡Momentum
Momentum is a measure of the quantity of motion of an object, which is the product of its mass and velocity. In quantum mechanics, momentum is related to the wave function through the de Broglie hypothesis, which states that particles have wave-like properties and their momentum is related to the wavelength of the wave associated with them. In the video, the momentum of a particle is equated to the momentum of a photon in the context of the wave function.
💡H-bar
H-bar (or h-bar) is a fundamental constant in quantum mechanics, which is the reduced form of Planck's constant (h). It is used in various equations, including the relation between energy and frequency (E=hf) and the de Broglie wavelength (lambda=h/p). In the video, h-bar is used to express the momentum of a particle in terms of its wave-like properties.
💡Energy Conservation
Energy conservation is a fundamental principle in physics stating that the total energy in an isolated system remains constant. It implies that energy can neither be created nor destroyed, only transformed from one form to another. In the video, this principle is applied to show that the total energy of the particle is conserved and is equal to its kinetic energy when potential energy is zero.
💡Quantum State
A quantum state is a specific condition or configuration of a quantum system. It is described by a wave function in quantum mechanics, which contains all the information about the system. The quantum state can be an eigenstate or a superposition of several eigenstates, and it evolves over time according to the Schrödinger equation. In the video, the quantum state of the system is being analyzed through the time-independent Schrödinger equation.
Highlights

The discussion begins with a time-independent equation, setting the stage for a wave function exercise.

The wave function in question depends solely on position, simplifying the scenario by assuming a single-dimensional motion of a particle with mass M and zero potential energy.

The first step in the exercise is to find the second derivative of the wave function with respect to X.

The first derivative of the wave function is derived, involving the cosine and sine functions of KX.

The second derivative calculation reveals a relationship between the wave function and its original form.

Substitution of the second derivative into the equation is discussed, leading to the identification of the particle's energy.

The potential energy is confirmed to be zero, simplifying the equation to relate only kinetic energy and the wave function.

The kinetic energy is expressed in terms of momentum, leading to an equation relating H-bar squared, K squared, and the particle's mass.

The energy equation is reformulated to express the total energy as the momentum squared divided by twice the mass.

The wave function is validated by showing that the left side of the equation equals the right side, confirming its correctness.

The momentum of a photon is equated to H-bar times K, drawing a parallel with the particle's momentum.

The exercise concludes by demonstrating the wave function's suitability for the time-independent Schrödinger equation for a one-dimensional particle.

The process of deriving and validating the wave function is outlined, providing a clear methodology for solving similar problems.

The use of trigonometric functions in deriving the wave function's derivatives is highlighted.

The importance of correctly applying the second derivative in the context of the wave equation is emphasized.

The role of H-bar in the energy equation is clarified, with a correction made to ensure the equation's accuracy.

The practical application of the wave function in understanding the behavior of particles in one dimension is discussed.

Transcripts

Browse More Related Video

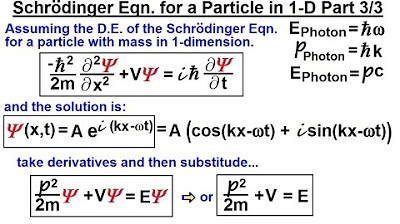
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (7 of 92) The Schrodinger Eqn. in 1-D (3/3)

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (5 of 92) The Schrodinger Eqn. in 1-D (1/3)

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (14 of 92) Time & Position Dependencies 3/3

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (6 of 92) The Schrodinger Eqn. in 1-D (2/3)

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (20 of 92) Particle in 1-D Box: Example 2/2

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (18 of 92) Particle in 1-D Box: Gen. Appr.

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
QuantumMechanicsSchrodingerEqWaveFunctionZeroPotentialOneDimensionKineticEnergyMomentumRelationPhotonMomentumEnergyEquivalenceMathDerivation