Standard Normal Distribution Tables, Z Scores, Probability & Empirical Rule - Stats

The Organic Chemistry Tutor

27 Oct 201951:03

EducationalLearning

32 Likes 10 Comments

TLDRThis statistics video explains key concepts like the standard normal distribution, represented by a bell curve with parameters mean and standard deviation. It covers formulas to calculate z-scores and data values, the empirical rule to determine percentages under the curve, using z-tables to find probabilities, and solving problems to find probabilities of IQ scores and defective tires. Overall, it aims to provide the formulas, concepts, and problem solving approaches needed to put the standard normal distribution to use for statistical analysis.

Takeaways

😀 The normal distribution is bell-shaped, with key parameters mean and standard deviation
😃 Z-scores indicate how many standard deviations from the mean; positive Z is above, negative is below
📏 Use formulas to calculate Z-scores and original X values from mean/standard deviation
📊 The empirical rule says 68/95/99.7% of values are within 1/2/3 standard deviations
📈 Use Z-tables to find area under normal curve and probabilities when Z isn't an integer
👩‍🏫 Explained how to apply empirical rule and Z-tables to IQ test score examples
🔬 Gave example problem applying normal distribution to defective product sampling
🧮 Showed calculations for mean/standard deviation of defective items using formula
📉 Demonstrated finding probability X is less/greater than value using Z-scores
✅ Wrapped up summarizing key normal distribution concepts covered in video

Q & A

What is the shape of a normal distribution?
-The normal distribution has the shape of a bell curve.
What are the two important parameters of a normal distribution?
-The two important parameters of a normal distribution are the mean and the standard deviation, represented by the Greek letter sigma (σ).
Where is the mean located on the bell curve of a normal distribution?
-The mean is located right in the middle of the bell curve.
What is the formula for calculating a z-score?
-The formula for calculating a z-score is: Z = (X - μ) / σ. Where X is the data point, μ is the mean, and σ is the standard deviation.
What does the empirical rule state about the percentage of values within 1, 2, and 3 standard deviations of the mean?
-The empirical rule states that approximately 68% of values lie within 1 standard deviation of the mean, 95% within 2 standard deviations, and 99.7% within 3 standard deviations.
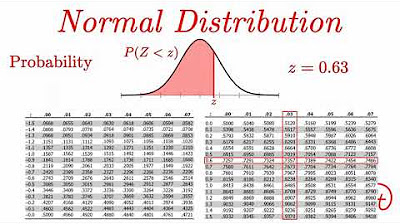
When would you need to use a standard normal distribution table?
-You would need to use a standard normal distribution table when you have z-scores that are not whole numbers and you cannot apply the empirical rule. The table allows you to find probabilities for fractional z-scores.
What is the difference between positive and negative z-scores?
-Negative z-scores correspond to data values below the mean. Positive z-scores correspond to data values above the mean.
How can you calculate the x value given a z-score?
-You can calculate the x value using: X = μ + Zσ, where μ is the mean, σ is the standard deviation, and Z is the z-score.
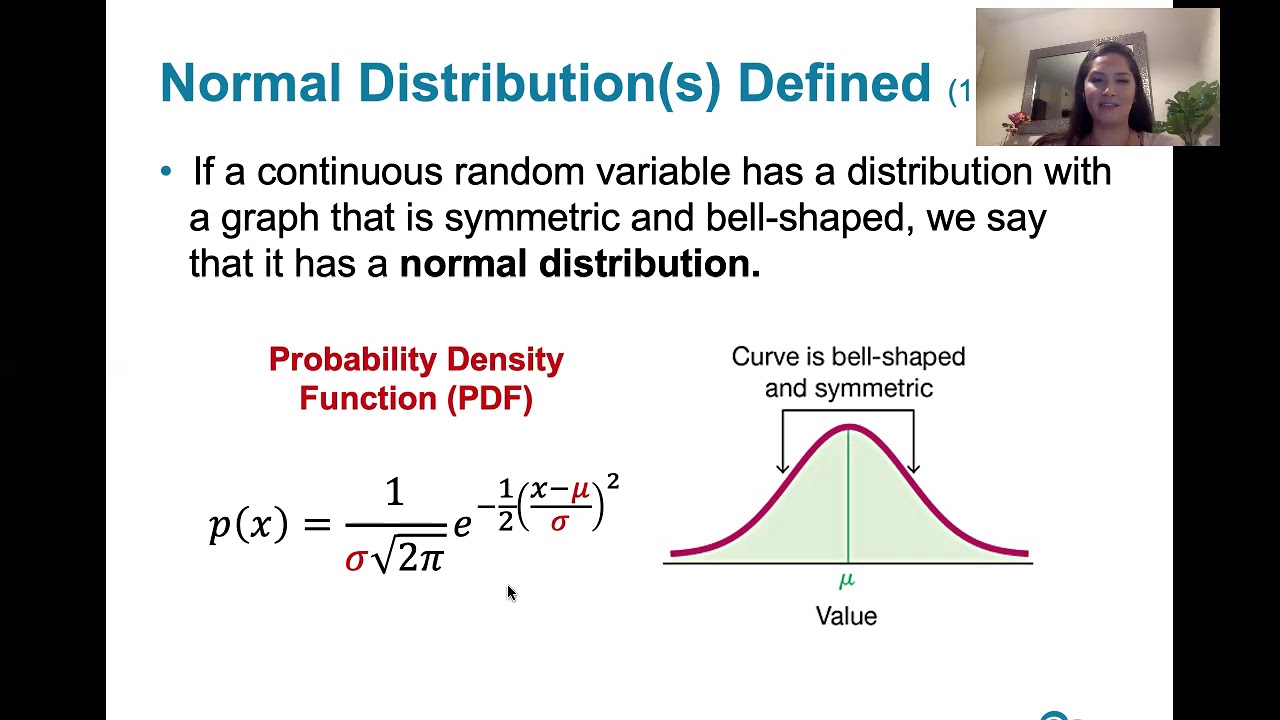
What does the probability density function formula represent?
-The probability density function formula represents the function that describes the relative likelihood of a random variable taking on a given value. For a normal distribution, it shows the probabilities across the range of z-scores.
How do you calculate the area between two x values on a normal distribution?
-Take the difference between the area under the curve up to the upper x value and the area under the curve up to the lower x value. This gives you the area between those two x values.

Outlines

00:00

😀 Introducing the standard normal distribution and key formulas

Overview of the standard normal distribution represented by a bell curve. Introduces parameters like mean and standard deviation. Explains z-scores and formulas to calculate them along with x values. Mentions the probability density function.

05:04

😃 Explaining the empirical rule for normal distributions

The empirical rule states percentages of data within 1, 2, and 3 standard deviations from the mean. Explains how to calculate area percentages under the curve using this rule.

10:05

😊 Positive and negative z-scores in relation to the mean

Positive z-scores are values above the mean, negative z-scores are below. Shows this on a number line with an example.

15:16

🙂 Solving an example problem using empirical rule

Goes through a sample problem step-by-step about test scores and a statistics class. Applies empirical rule to calculate probabilities.

20:18

🤓 Using z-tables to find areas under the curve

When z-scores are decimals, can't use empirical rule. Have to use z-tables to get area under curve and probabilities instead.

25:22

😎 IQ score example problem with z-tables

Works through a question with normally distributed IQ scores using z-tables to calculate various probabilities.

30:23

🧐 Determining IQ range for a percentile interval

Shows how to find IQ score range covering the middle 30% of the distribution, mapping percentiles to areas under curve.

35:25

🤔 Tire manufacturing sample problem with defects

Statistics example dealing with probabilities around defective tires from a manufacturing process.

40:26

😥 Calculating probability tires are defective

Continues tire defect example by finding probabilities for different counts of defective tires.

45:33

😌 Wrap up and conclusion

Final paragraph closes video, stating it's the end and hopes viewers found it helpful.

Mindmap

Keywords

💡normal distribution

The normal distribution, also known as the Gaussian distribution or bell curve, is a probability distribution used to represent real-valued random variables. In the video, it refers to the theoretical distribution of variables like IQ scores and test scores. The normal distribution has a symmetric, bell-shaped curve with a single peak. About 68% of values fall within 1 standard deviation of the mean.

💡standard deviation

The standard deviation, represented by the Greek letter sigma, is a measure of spread or variability around the mean. A low standard deviation indicates values are clustered close to the mean, while a high standard deviation indicates greater variation. In the IQ example, the standard deviation is 15 points.

💡z-score

The z-score represents the number of standard deviations a data point lies above or below the mean. Positive z-scores are above the mean, negatives are below. Z-scores allow comparison across data sets and are used to find probability areas under the normal curve.

💡empirical rule

The empirical rule uses the properties of the normal distribution to estimate percentages of values within 1, 2, and 3 standard deviations of the mean. For example, about 68% of values fall within ±1 standard deviation. This allows quick probability estimates without using z-score tables.

💡probability density function

The probability density function (PDF) gives the relative likelihood of a random variable taking on a given value. The video shows the PDF formula for the normal distribution. While not shown, it relies on calculus to determine probability areas under the curve.

💡mean

The mean, commonly called the average, is the central value in a data set calculated by summing all observations and dividing by the number of observations. In symmetric distributions like the normal distribution, the mean coincides with the peak of the curve.

💡percentile

A percentile represents the percentage of values below a given amount. For example, the 90th percentile means 90% of values fall at or below that data point. Percentiles are useful for comparing relative standing.

💡z-table

Z-tables allow you to look up the probability area under the normal curve for a given z-score. It provides the area under the curve to the left of the z-score. Z-tables eliminate the need for calculus when working with the normal distribution.

💡standard normal distribution

The standard normal distribution is a normal distribution with a mean of 0 and standard deviation of 1. By converting z-scores using the standard normal, probability areas can be looked up on a standard table for any normal distribution.

💡variance

The variance measures how far data points spread from their average value. It is calculated by taking the average of the squared deviations about the mean. The positive square root of the variance equal to the standard deviation.

Highlights

The normal distribution has the shape of a bell curve

The mean is right in the middle of the bell curve

Negative z-scores are below the mean and correspond to x values below the mean

The empirical rule tells percentages of data within 1, 2, and 3 standard deviations of the mean

You can calculate x given z using: x = mean + z * standard deviation

Use z-tables to find area under normal curve and probabilities when z-score isn't a whole number

Subtract areas under curve from z-tables to find probability x is between two values

Convert percentage to decimal to find number of occurrences from total population

Percentiles relate to area under curve; use z-table to convert between them

Mean defects = sample size x defect probability

Standard deviation defects = square root(sample size x defect probability x non-defect probability)

Probability x < value: (value - mean) / standard deviation, look up z-score in table

Probability x > value: 1 - Probability(x ≤ value)

Probability x between values: Probability(x ≤ upper value) - Probability(x ≤ lower value)

Relate z-scores, x-values, areas under curve, and probabilities to solve problems

Transcripts

Browse More Related Video

Elementary Statistics - Chapter 6 Normal Probability Distributions Part 1

Elementary Stats Lesson #11

6.1.3 The Standard Normal Distribution - Normal Dist. and Properties of the Standard Normal Dist.

6.1.0 The Standard Normal Distribution - Lesson Overview, Learning Outcomes

Normal Distribution EXPLAINED with Examples

ck12.org normal distribution problems: z-score | Probability and Statistics | Khan Academy