Chebyshev's Theorem

The Organic Chemistry Tutor
26 May 202012:49
EducationalLearning
32 Likes 10 Comments

TLDRThis video explains Chebyshev's theorem, which gives the minimum proportion of data within K standard deviations of the mean in any distribution. It compares Chebyshev's theorem to the empirical rule for normal distributions. After explaining the theorem, it applies Chebyshev's theorem to solve a word problem about weights in a city, first finding the minimum percentage within a weight range, then using that to calculate the minimum number of residents meeting that criteria given the city's population.

Takeaways
  • ๐Ÿ˜€ Chebyshev's theorem gives the minimum proportion of data within K standard deviations of the mean
  • ๐Ÿ“Š The theorem works for any distribution, not just normal distributions
  • ๐Ÿ“ Use the formula 1/(1+K^2) to calculate the minimum proportion for a given K value
  • ๐Ÿ“ˆ For normal distributions, percentages within 1, 2, and 3 standard deviations can be calculated empirically
  • ๐Ÿ”ข For non-normal distributions, Chebyshev's theorem gives a minimum bound
  • ๐Ÿ–Š To apply the theorem, calculate K based on the mean, standard deviation, and range values given
  • ๐Ÿ“ K is the same when the upper and lower bounds are equidistant from the mean
  • โœ… Once K is found, apply the formula to get the minimum percentage
  • ๐Ÿงฎ To get the minimum number within the range, multiply the percentage by the total population
  • i The actual percentage/number could be higher than Chebyshev's lower bound
Q & A

  • What is Chebyshev's theorem and what does it state?

    -Chebyshev's theorem is a statistical theorem that states that in any distribution, at least 1โˆ’1/k2 of the distribution's values are within k standard deviations of the mean, where k is any positive real number greater than 1.

  • How can Chebyshev's theorem be applied to both normal and non-normal distributions?

    -Chebyshev's theorem works for any distribution shape and allows you to determine the minimum percentage of data within k standard deviations of the mean, even when you don't know the exact distribution.

  • What is the main difference between using Chebyshev's theorem versus the empirical rule?

    -The empirical rule only applies to normal distributions and gives the exact percentage within 1, 2, and 3 standard deviations. Chebyshev's theorem works for any distribution but only provides a minimum bound, not the exact percentage.

  • What is the formula used in Chebyshev's theorem to calculate the minimum percentage within k standard deviations?

    -The formula is: Minimum Percentage = 1 - 1/k2, where k is the number of standard deviations from the mean.

  • How do you determine the k value needed to apply Chebyshev's theorem to a range?

    -To find k, take the endpoint further from the mean, subtract the mean, and divide by the standard deviation. This gives the number of standard deviations for that endpoint.

  • What information is needed to apply Chebyshev's theorem to the weight distribution problem?

    -You need the mean weight (170 lbs), standard deviation (10 lbs) and the weight range of interest (145-195 lbs first, then 140-200 lbs).

  • Once you've calculated the minimum percentage within k standard deviations, how do you get the minimum number of individuals?

    -Take the minimum percentage and multiply it by the total population. For example, 0.889 * 200,000 residents gave 177,800 as the minimum individuals within 3 standard deviations.

  • Why does Chebyshev's theorem provide the minimum rather than exact percentage within k standard deviations?

    -It applies to any distribution shape, and without knowing the exact distribution, it can only guarantee a minimum proportion based on mathematical proof.

  • What are some examples of when Chebyshev's theorem would be useful over the empirical rule?

    -Chebyshev's theorem is useful when dealing with non-normal data such as skewed or multimodal distributions where the empirical rule for normal distributions doesn't apply.

  • What additional insights does Chebyshev's theorem provide over only using the mean and standard deviation?

    -It allows you to make probabilistic statements about the proportion of data within a given range, not just the central tendency and spread.

Outlines
00:00
๐Ÿ˜€ Introducing Chebyshev's Theorem and how to apply it

This paragraph introduces Chebyshev's theorem, which gives the minimum proportion of data within K standard deviations of the mean in any distribution. It explains how to calculate this proportion using the formula 1/(1-K^2). It compares applying Chebyshev's theorem versus the empirical rule to find the percentage within certain standard deviations for normal versus non-normal distributions.

05:02
๐Ÿ˜ƒ Using Chebyshev's theorem to solve a sample problem

This paragraph applies Chebyshev's theorem to solve a sample problem asking for the minimum percentage and number of individuals in a city with weight between given bounds, given the mean and standard deviation. It shows step-by-step how to calculate K and apply the Chebyshev formula.

10:04
๐Ÿ˜Š Extending solution to slightly modified sample problem

This paragraph extends the solution to a tweak of the original sample problem, now asking for the minimum number of individuals within a slightly different weight range. It re-calculates K for the new range and applies the steps from the previous example to get the final numerical answer.

Mindmap
Keywords
๐Ÿ’กChebyshev's theorem
Chebyshev's theorem is a statistical theorem that gives a lower bound on the proportion of data within a certain number of standard deviations from the mean. It works for any distribution. In the video, it is used to calculate the minimum percentage of individuals within a given weight range without knowing the distribution.
๐Ÿ’กstandard deviation
The standard deviation is a measure of dispersion that shows how spread out the data is from the mean. Chebyshev's theorem calculates the minimum percentage within a certain number of standard deviations. A smaller standard deviation indicates the data is clustered closer to the mean.
๐Ÿ’กnormal distribution
A normal distribution is a symmetrical bell-shaped distribution where 68% of values fall within 1 standard deviation of the mean. It allows you to use the empirical rule to calculate percentages within 1, 2, or 3 standard deviations.
๐Ÿ’กempirical rule
The empirical rule is a shorthand used with normal distributions, stating 68% of values fall within 1 standard deviation, 95% within 2 standard deviations, and 99.7% within 3 standard deviations of the mean.
๐Ÿ’กnon-standard distribution
A non-standard or unusual distribution does not follow the normal distribution. You cannot rely on the empirical rule and instead must use Chebyshev's theorem to calculate minimum percentages within standard deviations.
๐Ÿ’กmean
The mean, commonly called the average, is the central tendency calculated by summing all values and dividing by the number of values. In the problem, the mean weight is critical to calculate K and apply Chebyshev's theorem.
๐Ÿ’กminimum percentage
Chebyshev's theorem gives the minimum percentage within a number of standard deviations, allowing you to establish a lower bound. The actual percentage could be higher for an unusual distribution.
๐Ÿ’กminimum amount
After finding the minimum percentage using Chebyshev's theorem, the video shows how to use the percentage and total population to get the minimum number of individuals meeting the weight criteria.
๐Ÿ’กsample population
The example uses City XYZ with 200,000 residents as the sample population whose weight distribution is being analyzed using statistical tools like the mean and Chebyshev's theorem.
๐Ÿ’กprobability
At the end, the video relates the minimum percentage from Chebyshev's theorem to a probability representing the chance a resident falls in the weight range. This probability has a lower bound of >= 0.89 but could be higher.
Highlights

Chebyshev's theorem gives the minimum proportion of data within K standard deviations of the mean.

Chebyshev's theorem works for any type of distribution, not just normal distributions.

Chebyshev's theorem provides a lower bound, not an exact percentage within K standard deviations.

For non-normal distributions, use Chebyshev's theorem instead of the empirical 68-95-99.7 rule.

Calculate K to determine the number of standard deviations from the mean using: K = (X - ฮผ) / ฯƒ

For the weight range 145-195 lbs, K = 2.5. So at least 84% fall within 2.5 standard deviations.

For the wider range 140-200 lbs, K = 3. So at least 88.9% fall within 3 standard deviations.

To get the minimum number of individuals, multiply the minimum percentage by the population size.

Chebyshev's theorem lets you calculate a minimum percentage within any interval, for any distribution.

It assumes only that the distribution has finite mean and standard deviation.

Provides a lower bound on the percentage within a given number of standard deviations.

More precise than assuming a normal distribution when you don't know the distribution.

Can be used along with the empirical rule for normal distributions when applicable.

Limits how far from the mean the distribution can stretch, no matter how non-normal.

Simple and versatile tool for analyzing unknown distributions.

Transcripts

Browse More Related Video

Statistics - How to use Chebyshev's Theorem

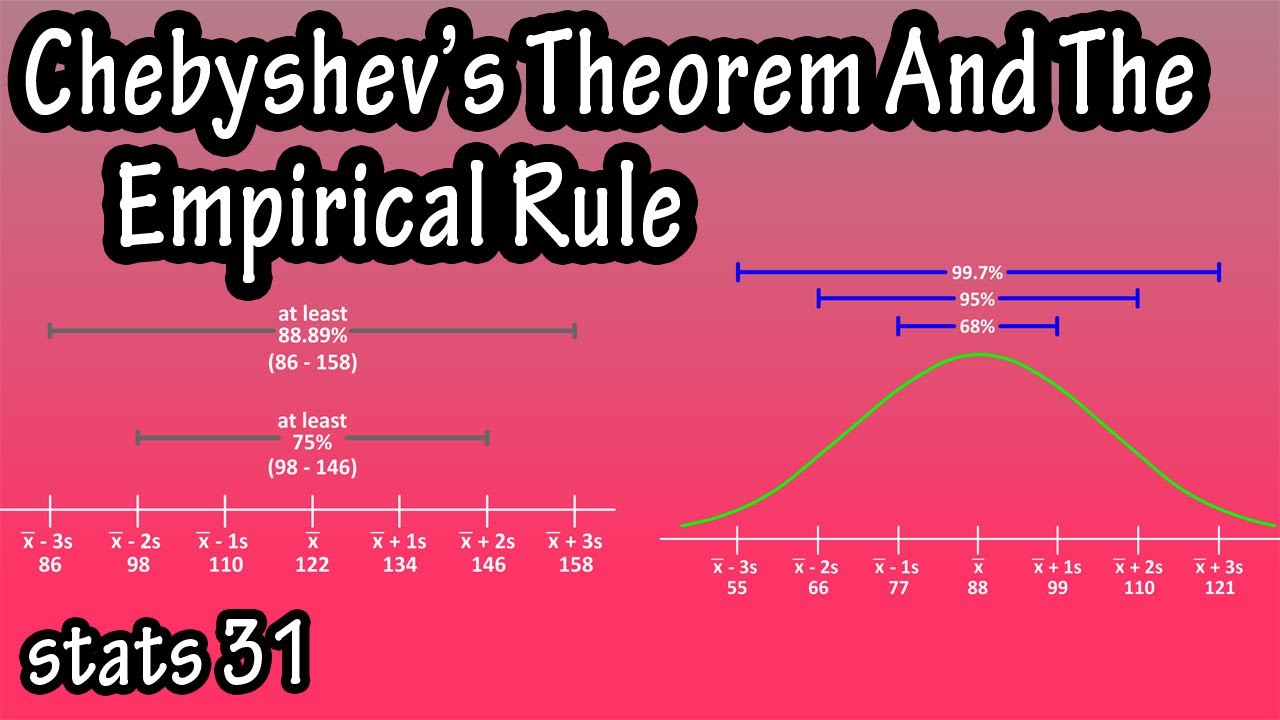
What Is And How To Use Chebyshev's Theorem And The Empirical Rule Formula In Statistics Explained

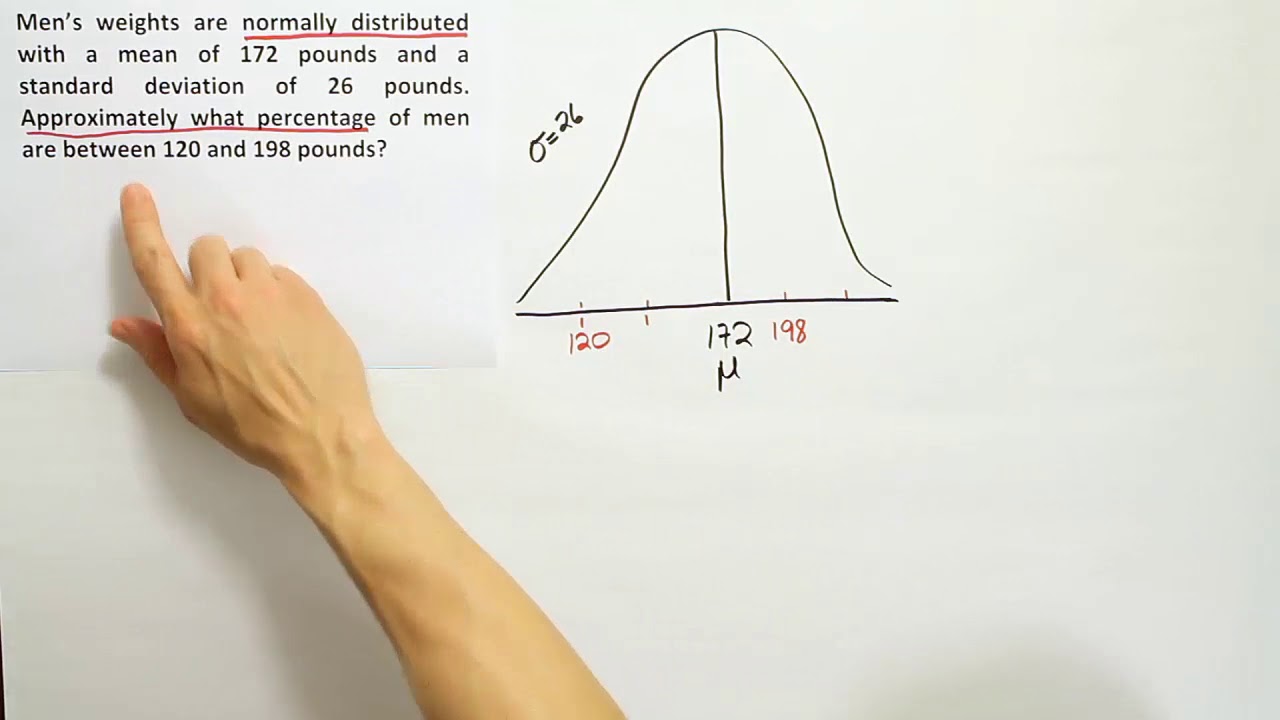
Applying the empirical rule to an example that uses an interval that is not symmetric

Statistics - How to use the Empirical Rule

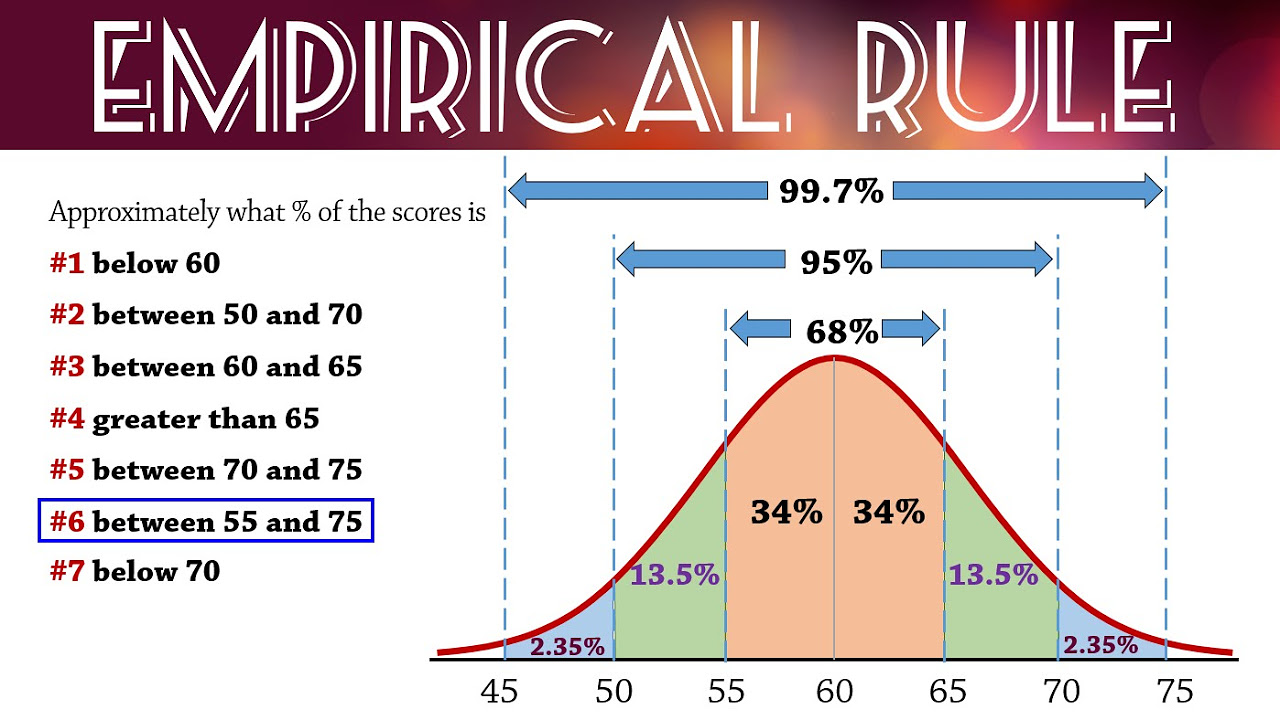
Empirical Rule (68-95-99.7) for Normal Distributions

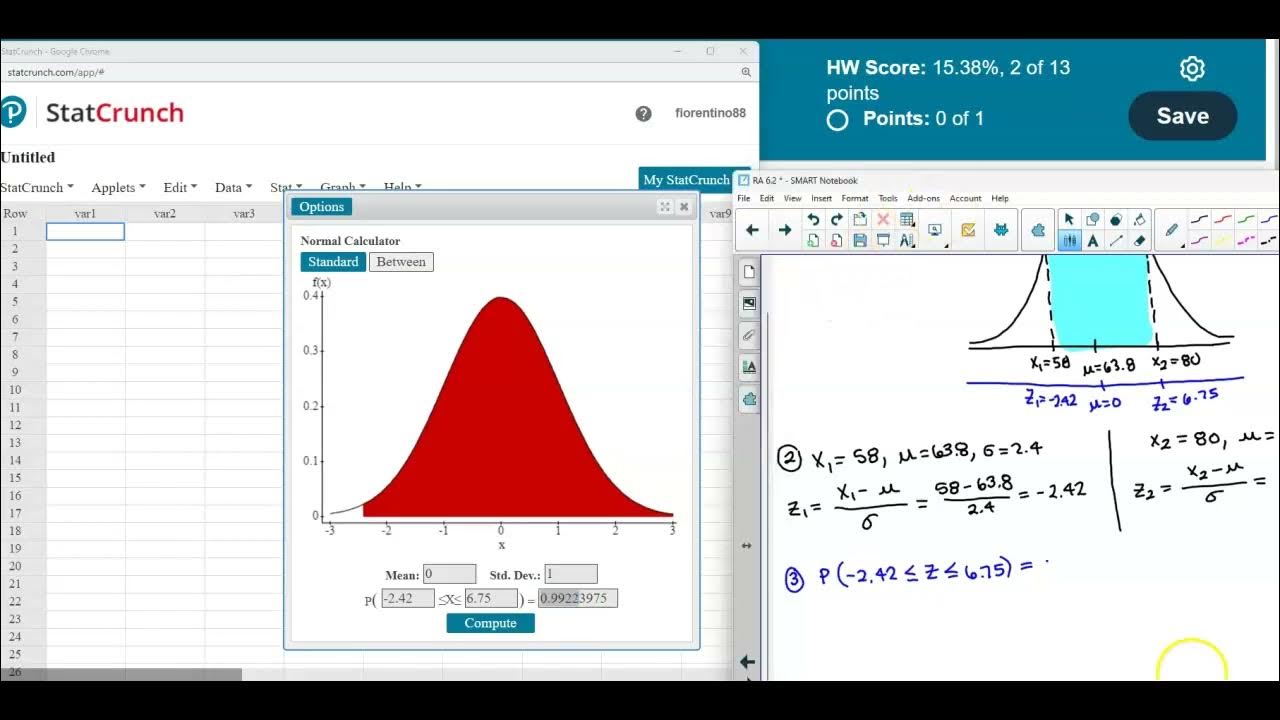
Math 14 6.2.25 Find the percentage of women meeting the height requirement.

Rate This

5.0 / 5 (0 votes)

Thanks for rating: