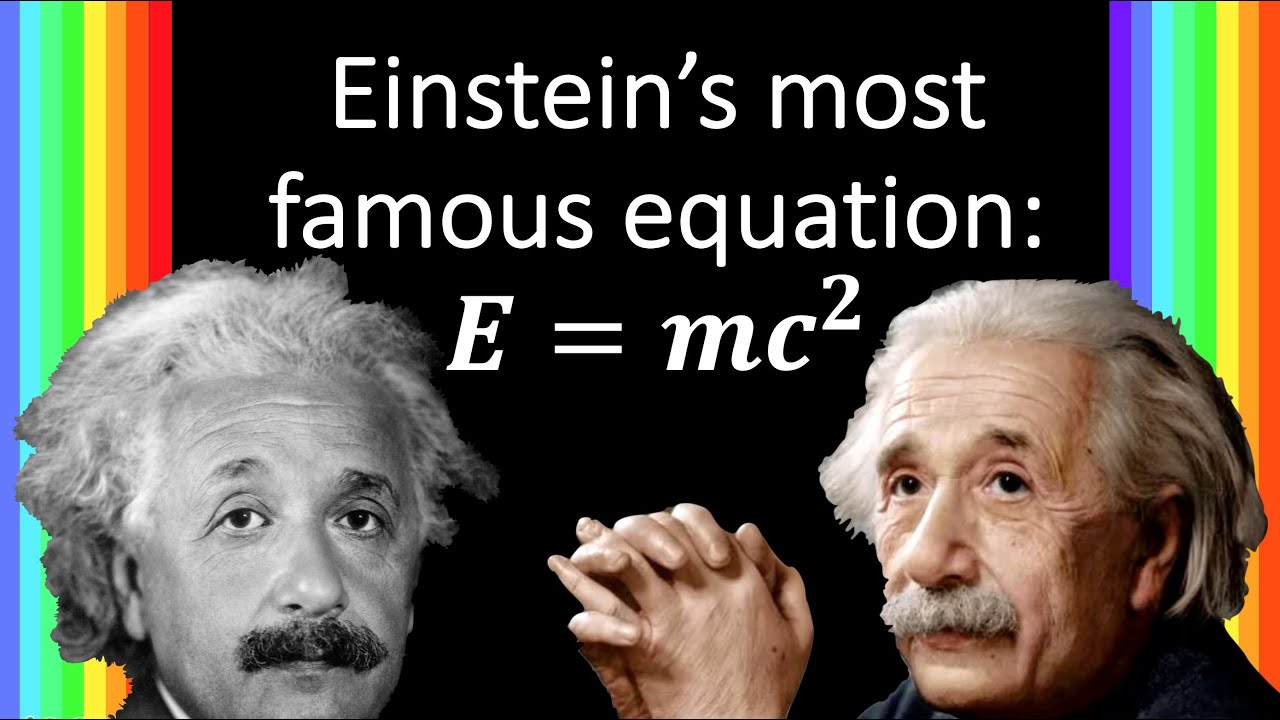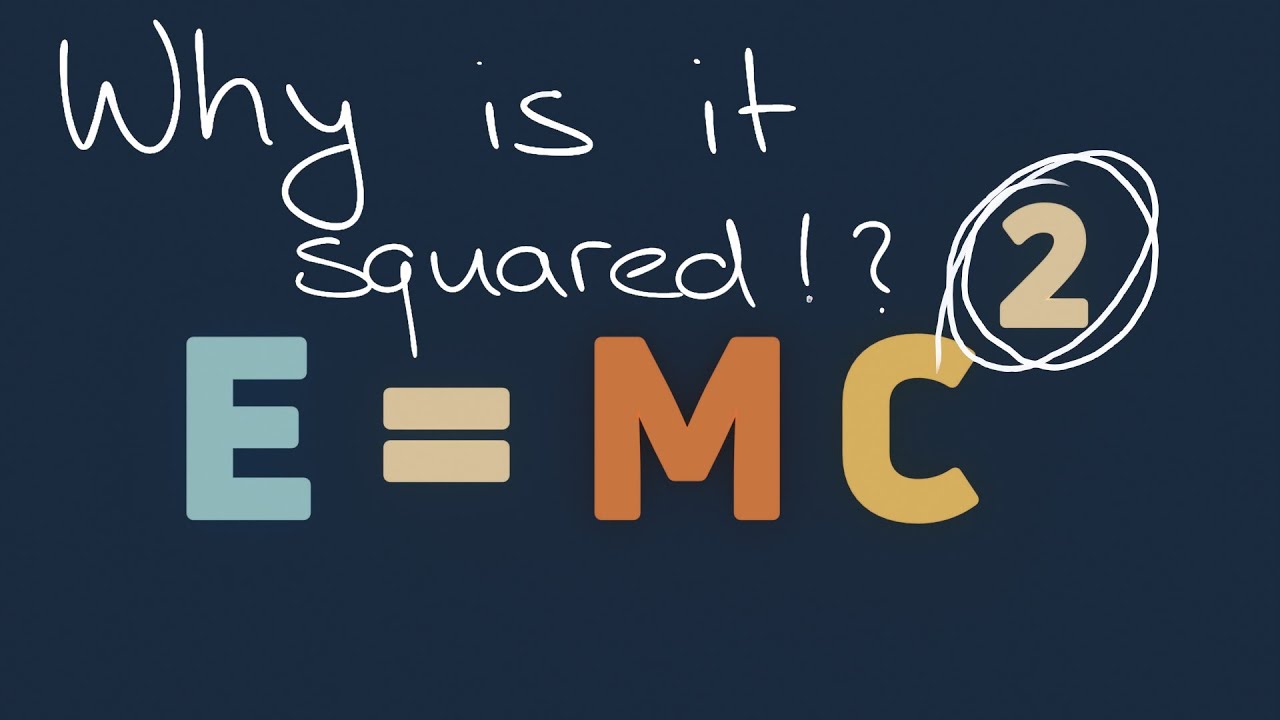Special Relativity | Lecture 3
TLDRThe video script is an in-depth lecture on particle mechanics within the context of the special theory of relativity. It begins by discussing the behavior of particles and their movement, introducing key concepts such as momentum, energy, and the famous equation E=mc^2. The lecturer emphasizes the importance of approximations for velocities close to the speed of light and delves into the mathematical formulations that arise when objects approach relativistic speeds. The concept of the binomial theorem is applied to demonstrate how relativistic formulas can be approximated to non-relativistic ones for slow-moving objects. The lecture also explores the principles of least action and the Lagrangian and Hamiltonian mechanics, which are instrumental in deriving the equations of motion for particles. The Hamiltonian for a relativistic particle is derived, and the conservation of four-momentum is discussed, leading to the identification of energy as the fourth component of momentum. The script concludes with an exploration of the relationship between mass, energy, and momentum, particularly highlighting the case of massless particles like photons and the concept of energy in terms of momentum. The lecture is rich in mathematical details and provides a solid foundation for understanding the intricacies of relativistic mechanics.
Takeaways
- 📚 The special theory of relativity discusses how particles move and introduces concepts like momentum, energy, and the famous equation E=mc^2.
- 📐 To reconcile relativistic formulas with non-relativistic ones, approximations are made for slow velocities, using the binomial theorem to expand and simplify expressions.
- 🌌 When objects move slowly compared to the speed of light, relativistic mechanics reduces to Newtonian mechanics, showing the connection between classical and relativistic physics.
- 🚀 The four-momentum is a vector quantity in special relativity that includes the energy of an object at rest (rest mass times the speed of light squared) and its spatial momentum.
- ⏲️ Proper time is an invariant quantity that all observers agree upon, and it is used in the calculation of the action, a central concept in the principle of least action.
- 🔍 The principle of least action states that the path taken by a particle between two points in spacetime is the one that minimizes the action, leading to the equations of motion.
- 📉 The action in relativistic mechanics is an integral over the proper time along the path of a particle, and it is invariant under Lorentz transformations.
- 🤔 The four-velocity is a four-vector that describes the motion of a particle in spacetime, and it has a relationship with the ordinary velocity as the particle's velocity approaches the speed of light.
- ⚖️ Momentum conservation is a consequence of translation invariance and is maintained in relativistic mechanics, with the four-momentum being conserved in spacetime.
- 💫 The energy of a particle in relativistic mechanics is not just its kinetic energy but also includes its rest mass energy, leading to the equation E=mc^2, which shows the equivalence of mass and energy.
- ✨ For massless particles like photons, their energy is given by the magnitude of their momentum multiplied by the speed of light, which is a direct application of the E=mc^2 principle.
Q & A
What is the main topic of discussion in the provided transcript?
-The main topic of discussion is particle mechanics within the special theory of relativity, focusing on concepts such as momentum, energy, and the behavior of particles as they approach the speed of light.
What is the significance of the binomial theorem in the context of the script?
-The binomial theorem is used to approximate the expression 1 - v^2 for small velocities, which is crucial for deriving the non-relativistic limit of relativistic formulas and understanding how relativistic mechanics reduces to Newtonian mechanics at low speeds.
How does the concept of four-velocity relate to our classical understanding of velocity?
-Four-velocity is a four-dimensional generalization of classical velocity. It includes three space components and one time component. In the non-relativistic limit, where velocities are much smaller than the speed of light, the space components of four-velocity reduce to the classical velocity.
What is the principle of least action, and how does it apply to the motion of particles?
-The principle of least action is a fundamental concept in physics that states that the trajectory of a particle between two points is the one that minimizes the action, a quantity that is invariant across different reference frames. This principle is used to derive the equations of motion for particles in various physical theories, including relativistic mechanics.
What is the relationship between the energy of a moving object and its rest mass?
-According to the special theory of relativity, the energy of a moving object is given by E = mc^2, where E is the energy, m is the rest mass, and c is the speed of light. This equation, often associated with Einstein, shows that the energy of an object increases with its velocity and is directly proportional to its rest mass.
How does the concept of proper time relate to the spacetime interval?
-Proper time is the time experienced by an observer moving along a specific worldline in spacetime. It is derived from the spacetime interval, which is invariant and does not change with different inertial frames of reference. The proper time is the square root of the spacetime interval, given by Δτ^2 = Δt^2 - Δx^2, where Δτ is the proper time, Δt is the time interval, and Δx is the spatial interval.
What is the significance of the term 'four-momentum' in the context of special relativity?
-Four-momentum is a four-vector that combines the spatial momentum of a particle with its energy, effectively unifying these concepts into a single framework. It is conserved in relativistic mechanics, just as momentum is conserved in classical mechanics, and it is crucial for understanding the behavior of particles in high-energy physics.
How does the script illustrate the transition from classical to relativistic mechanics?
-The script illustrates this transition by showing how classical mechanics formulas, such as those for momentum and kinetic energy, are embedded within their relativistic counterparts. It demonstrates how, in the limit of low velocities, relativistic mechanics reduces to Newtonian mechanics, thus bridging the gap between the two frameworks.
What is the role of the speed of light in the context of special relativity?
-The speed of light (c) is a fundamental constant in special relativity. It sets the upper limit for the speed at which information or matter can travel. Many of the formulas and concepts discussed in the script, such as four-velocity and the energy-momentum relation, involve the speed of light and highlight its central role in the theory.
How does the script address the concept of mass in special relativity?
-The script discusses mass in the context of relativistic mechanics, emphasizing that mass, as represented by the rest mass, is a property of a particle that remains constant regardless of its state of motion. It also touches upon the concept of relativistic mass, which increases with the velocity of the particle.
What is the significance of the square root of 1 - v^2/c^2 in the context of the script?
-The square root of 1 - v^2/c^2 is a factor that appears in various relativistic formulas, such as those for four-velocity and the relativistic Lagrangian. It accounts for the fact that the spacetime interval (and thus proper time) is affected by the relative velocity of the observer and the particle, ensuring that these quantities remain invariant across different inertial frames.
Outlines
📐 Introduction to Particle Mechanics and Relativity
The speaker begins by introducing the topic of particle mechanics within the framework of special relativity, focusing on how particles move and the concepts of momentum and energy. The aim is to delve into Einstein's famous equation, E=mc², and to connect the relativistic formulas to their non-relativistic counterparts under conditions of slow motion. The binomial theorem is highlighted as a mathematical tool for approximations at low velocities.
🔍 Approximations and Classical Physics
The discussion moves towards approximations for the quantity 1 - v^2/c^2, which is pivotal in showing the transition from relativistic to classical mechanics. The binomial theorem is used to expand this expression and to illustrate how the zeroth and first-order terms become significant in the context of small velocities. The importance of the first-order term for non-relativistic velocities is emphasized, and classical physics tools are shown to emerge from this limit.
🚀 Particles and Their Motion
The concept of a particle is explored, which can range from elementary particles to macroscopic objects like a sun or a donut. The position of a particle is typically defined by its center of mass. The speaker discusses how the mechanics of particle motion are governed by Newtonian mechanics, and how momentum and kinetic energy are defined in this context. It is also noted that internal energies, such as chemical energy in a donut, are not dependent on the object's state of motion.
⏳ Classical Mechanics and the Principle of Least Action
The speaker revisits classical mechanics, particularly the principle of least action, Lagrangian, and canonical momenta. The principle of least action is tied to the idea of a trajectory in SpaceTime, emphasizing the concept of a world line for a particle. The invariant proper time between two points in SpaceTime is defined, and the conditions for time-like and space-like intervals are discussed, including the relativity of simultaneity.
🧮 Four-Dimensional Space-Time and Trajectories
The focus shifts to four-dimensional SpaceTime and the properties of intervals within it. The distinction between time-like and space-like intervals is further elaborated, with the implication that particles move on time-like trajectories, adhering to the universal speed limit set by the speed of light. The concept of four-velocity is introduced, and its components are discussed in relation to the ordinary velocity.
🌌 Relativistic Velocity and Four-Velocity
The relationship between four-velocity and ordinary velocity is explored, highlighting the non-relativistic limit where the two notions converge. The components of four-velocity are shown to be not entirely independent, with the space components being related to the time component through a single relationship. The significance of the four-velocity in characterizing the motion of a particle is emphasized.
🎯 Principle of Least Action and Relativistic Mechanics
The principle of least action is applied to derive the laws governing the motion of a free particle in relativistic mechanics. The action is constructed as an integral over the trajectory of the particle, using proper time as the invariant quantity. The Lagrangian for a relativistic free particle is formulated, and the connection between the relativistic and non-relativistic Lagrangians is discussed.
🚨 Momentum and Energy in Relativistic Context
The concepts of momentum and energy are revisited in the context of relativistic mechanics. The momentum is identified as conserved due to translation invariance, and its components are derived from the Lagrangian. The energy of a particle is related to its momentum and mass, leading to the introduction of the concept of rest mass and the invariant mass of a particle.
🧲 Four-Vector and Conservation Laws
The properties of four-vectors are discussed, emphasizing that statements about the components of a four-vector must be invariant to be physically meaningful. The conservation of momentum is extended to the concept of four-momentum, which includes energy as its time component. The Hamiltonian is introduced as a means to identify the conserved quantities in the system.
🌟 Energy, Momentum, and Mass
The relationship between energy, momentum, and mass is further explored, leading to the famous equation E=mc². The energy of a system at rest is identified as its rest energy, and the conversion between mass and energy is discussed. The concept of massless particles is introduced, and it is shown that their energy can be expressed in terms of their momentum.
🤔 Questions and Answers on Relativistic Decay
The speaker addresses questions regarding the conservation of spin, the decay of positronium into two photons, and the implications of these processes in relativistic physics. The discussion touches on the experimental verification of decay processes, the role of quantum mechanics, and the conversion of mass into energy.
🔬 Relativistic Equations and Newton's Laws
The content of the Euler-Lagrange equations in the context of relativistic mechanics is summarized, emphasizing that they reduce to the conservation of momentum and energy, leading to straight-line motion in SpaceTime. The distinction between the limits of relativistic and quantum mechanics is clarified, and the potential for both relativistic and quantum mechanical descriptions of a system is acknowledged.
Mindmap
Keywords
💡Particle Mechanics
💡Special Theory of Relativity
💡Momentum
💡Energy
💡Four-Velocity
💡Proper Time
💡Lagrangian
💡Hamiltonian
💡Relativistic Mass
💡Four-Momentum
💡Binomial Theorem
Highlights
Introduction to particle mechanics in the special theory of relativity, focusing on how particles move and the concepts of momentum and energy.
Discussion on the famous equation E=mc^2 and its implications for understanding the relationship between energy and mass.
Explanation of the binomial theorem's role in approximating relativistic formulas for small velocities, connecting to non-relativistic formulas.
Derivation of the relativistic four-momentum, which combines mass, energy, and momentum into a single four-vector.
Illustration of how the relativistic theory of particle motion reduces to Newtonian mechanics for slow-moving objects.
Use of the principle of least action to derive the equations of motion for a free particle in the context of special relativity.
Calculation of the Hamiltonian for a relativistic particle, leading to insights about the energy of a particle in terms of its momentum.
Discussion on the concept of rest mass and how it is used in modern physics, distinguishing it from relativistic mass.
Explanation of how the energy of a system at rest is related to its inertial mass through the equation E=mc^2.
Analysis of the behavior of massless particles, such as photons, in terms of their momentum and energy.
Demonstration of how energy and momentum are conserved in particle decay processes, even when there is a change in rest mass.
Derivation of the energy of a massless particle in terms of the magnitude of its momentum vector, multiplied by the speed of light.
Application of the principles of special relativity to the decay of positronium into two photons, showcasing mass-to-energy conversion.
Discussion on the conservation of angular momentum in the decay process of particles, and how it affects the directions of emitted particles.
Exploration of the limits of applicability of classical mechanics and special relativity, and the transition between these frameworks.
Insight into the role of the speed of light as a conversion factor between different forms of defining energy.
Overview of the conditions under which the conservation laws of momentum and energy hold true in a laboratory setting.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: