Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (4 of 92) The Schrodinger Eqn. "Derived"

Michel van Biezen
20 Nov 201609:15
EducationalLearning
32 Likes 10 Comments

TLDRThe transcript discusses the derivation of the Schrödinger equation from classical wave mechanics, highlighting the leaps of faith taken in the process. It explains the transition from traditional wave equations to one that incorporates quantum mechanical concepts, such as energy and momentum. The lecture emphasizes the importance of experimental validation and how the Schrödinger equation has withstood scrutiny to become a fundamental tool in quantum mechanics for describing the behavior of particles.

Takeaways
  • 🌊 The traditional wave equation is introduced with amplitude, angular frequency, and wave number as key components.
  • 🔄 A leap of faith is necessary when deriving the wave equation due to the absence of a strictly mathematical approach in certain steps.
  • 🌀 The goal is to connect the classical wave equation to a format that can represent the Schrödinger equation.
  • 📈 The wave equation is manipulated by replacing variables and using conversions to relate to energy and momentum.
  • 🌌 The frequency and wavelength relationship for waves is utilized, with 2πF equal to Ω, the angular frequency.
  • 📊 The real and imaginary parts of the wave function are discussed, with the real part being relevant for classical waves and the imaginary part for quantum mechanics.
  • 💫 The energy of a particle is related to its frequency and wavelength through the de Broglie wavelength concept.
  • 🤔 A fundamental challenge is acknowledged when relating the energy of a photon to that of a particle, but a leap of faith is suggested to bridge this gap.
  • 🌟 The wave function is derived in terms of the energy and momentum of a particle and is time and position dependent.
  • 🎯 The validity of the wave equation is confirmed through experimental results over the years.
  • 🔍 The final derivation of the Schrödinger equation and its application in describing the motion of particles in quantum mechanics is promised to be discussed further.
Q & A

  • How does the traditional wave equation relate to the Schrödinger equation?

    -The traditional wave equation is used as a starting point to derive the Schrödinger equation by connecting the concepts of amplitude, angular frequency, and wave number to the energy and momentum of particles in quantum mechanics.

  • What is the significance of the angular frequency (Omega) in the wave equation?

    -The angular frequency (Omega) represents the rate of change of the wave's phase per unit time and is crucial in determining the periodic nature of the wave function.

  • What is the role of the wave number (K) in the context of the wave equation?

    -The wave number (K) is inversely proportional to the wavelength and is used to describe the spatial properties of the wave, such as its propagation and the number of cycles per unit length.

  • How is the frequency (F) related to the wavelength (lambda) in wave functions?

    -The frequency (F) times the wavelength (lambda) is equal to the wave's velocity, which is a fundamental relationship in wave physics.

  • What is the significance of the de Broglie wavelength in quantum mechanics?

    -The de Broglie wavelength is the wavelength associated with a particle and is inversely proportional to its momentum, as given by the equation lambda = h/P, where h is Planck's constant and P is the momentum of the particle.

  • How does the energy of a particle relate to its frequency in the context of quantum mechanics?

    -The energy of a particle is proportional to its frequency, as described by the equation E = hF, where E is the energy, h is Planck's constant, and F is the frequency of the particle.

  • What is the role of the imaginary unit (i) in the wave function?

    -The imaginary unit (i) is used in the wave function to allow for the representation of complex numbers, which are essential for describing the probability amplitudes in quantum mechanics.

  • What is the Hamiltonian in the context of the Schrödinger equation?

    -The Hamiltonian is a mathematical operator that represents the total energy of a system in quantum mechanics, including both kinetic and potential energy, and is used in the Schrödinger equation to describe the time evolution of the wave function.

  • How do experimental results validate the Schrödinger equation?

    -Experimental results have consistently supported the predictions made by the Schrödinger equation, confirming its validity in describing the behavior of quantum systems.

  • What is the significance of the leap of faith taken in the derivation of the Schrödinger equation?

    -The leap of faith refers to the assumptions made during the derivation, such as equating the energy of a photon with the energy of a particle, which were not directly justified but have been validated by experimental evidence.

  • How does the Schrödinger equation describe the motion of small particles in quantum mechanics?

    -The Schrödinger equation provides a mathematical framework to calculate the probability amplitude of finding a particle in a particular state, which, when squared, gives the probability distribution of the particle's position, momentum, and other physical properties over time.

Outlines
00:00
🌟 Introduction to Wave Equations and the Transition to Schrödinger Equation

This paragraph introduces the concept of deriving wave equations, acknowledging the leap of faith sometimes required in mathematical equations. The speaker outlines the plan to compare the traditional wave equation with the Schrödinger equation, explaining the general mechanical equation with amplitude, angular frequency, and wave number. The process of transforming the classical wave equation into a format that can represent the Schrödinger equation is detailed, including the use of energy and momentum conversions. The paragraph concludes with the realization that the frequency times the wavelength equals the velocity, leading to the wave equation in terms of velocity and time for position.

05:01
📝 Derivation of the Wave Function and Connection to Quantum Mechanics

The second paragraph delves into the derivation of the wave function, starting with the real and imaginary parts of a function and how they apply to real wave equations and quantum mechanics. The speaker discusses the energy and wavelength of a particle, introducing the de Broglie wavelength and its implications. The paragraph continues with the manipulation of variables to express the wave function in terms of the particle's energy and momentum, leading to the Schrödinger equation. The speaker emphasizes the importance of experimental validation of these equations and the fine line between photons and small particles, highlighting the leaps of faith taken in the development of quantum mechanics.

Mindmap
Keywords
💡Wave Equation
The wave equation is a fundamental mathematical model that describes the propagation of waves in a physical medium or in space. In the context of the video, it is used to describe the traditional wave equation, which is then compared and adapted to represent the Schrödinger equation in quantum mechanics. The wave equation is essential for understanding how waves, including light and sound, travel and interact with their environment.
💡Schrödinger Equation
The Schrödinger equation is a fundamental equation in quantum mechanics that describes how the quantum state of a physical system changes with time. It is used to calculate the probability distribution of particles in a system and is essential for predicting the behavior of quantum systems. In the video, the traditional wave equation is transformed to resemble the Schrödinger equation by incorporating quantum mechanical concepts such as energy and momentum.
💡Amplitude
Amplitude in the context of waves refers to the maximum displacement of a point on the wave from its equilibrium position. It is a measure of the wave's energy and is used in the wave equation to describe the wave's intensity. In the video, amplitude is used to describe the initial form of the wave equation, which is then modified to fit quantum mechanical principles.
💡Angular Frequency
Angular frequency, denoted by Omega, is a measure of how quickly a wave oscillates. It is the rate of change of the angle per unit time and is directly related to the frequency of the wave. In the wave equation, angular frequency determines the periodic nature of the wave and is crucial for calculating the wave's phase at any given time.
💡Wave Number
The wave number, denoted by K, is a measure of the spatial frequency of a wave, indicating the number of wave cycles per unit length. It is inversely proportional to the wavelength and is used in the wave equation to describe the spatial properties of the wave. The wave number is essential for understanding wave propagation and interference patterns.
💡Energy and Momentum
Energy and momentum are fundamental concepts in physics that describe the dynamic properties of objects. In quantum mechanics, these concepts are applied to particles, where energy is related to the frequency of a particle (E=hv) and momentum is related to its wavelength (p=h/λ). These relationships, known as the de Broglie relations, are crucial for the development of the Schrödinger equation and for understanding the behavior of particles at the quantum level.
💡Quantum Mechanics
Quantum mechanics is a branch of physics that deals with the behavior of particles at the atomic and subatomic scale. It is based on the principles of wave-particle duality and the superposition of states. The video focuses on the development of the Schrödinger equation, which is a cornerstone of quantum mechanics and is used to describe the quantum states of particles.
💡Leap of Faith
In the context of the video, a 'leap of faith' refers to the intuitive or hypothetical steps taken in the development of scientific theories when there is no direct empirical evidence or when the mathematical derivations involve assumptions. It is the act of proposing a theory or model based on reason and logic, even when the evidence is not yet available or conclusive.
💡Hamiltonian
The Hamiltonian is a function used in classical and quantum mechanics that represents the total energy of a system. In classical mechanics, it is the sum of kinetic and potential energies, while in quantum mechanics, it is the operator that corresponds to the energy observable. The Hamiltonian is crucial for understanding the dynamics of a system and for solving the Schrödinger equation.
💡de Broglie Wavelength
The de Broglie wavelength is a concept in quantum mechanics that relates the wavelength of a particle to its momentum. It is derived from the hypothesis that particles can exhibit wave-like properties, with the wavelength being inversely proportional to the momentum. This concept is fundamental in the development of the Schrödinger equation and the understanding of quantum behavior.
💡Experimental Validation
Experimental validation refers to the process of testing a scientific theory or model against empirical data to determine its accuracy and reliability. In the context of the video, it is the method by which the Schrödinger equation and other quantum mechanical models are confirmed to accurately describe the behavior of particles at the quantum level.
Highlights

The lecture discusses the derivation of the Schrödinger equation from traditional wave mechanics.

There is no assured, mathematically correct way to derive the equation, requiring a leap of faith in certain steps.

The traditional wave equation is compared and adapted to represent the Schrödinger equation.

The general mechanical wave equation is given with amplitude, angular frequency, and wave number.

The wave equation is manipulated to align with the classical wave form and further developed for energy and momentum representation.

The relationship between wave number (K) and angular frequency (Omega) is established using 2π/λ and 2πF.

The wave equation is rewritten in terms of velocity (V) and wavelength (λ), connecting it to quantum mechanics.

The real and imaginary parts of the wave function are discussed, with the imaginary part being essential for quantum mechanics.

The de Broglie wavelength of a particle is introduced, relating energy, wavelength, and Planck's constant.

A leap of faith is taken to apply the energy formula of a photon to a particle, despite fundamental differences.

The wave function is expressed in terms of energy, momentum, time, and position, aligning with the requirements for quantum mechanics.

The equation is further refined by replacing variables with energy and momentum expressions.

The final form of the wave function is derived, which is essential for introducing the Schrödinger equation.

The Hamiltonian is mentioned as a key component for describing the motion of particles in quantum mechanics.

The lecture emphasizes the importance of experimental validation of the derived equations.

The Schrödinger equation's validity is supported by years of experimental results.

The lecture promises to show the final derivation of the Schrödinger equation and its application in future content.

Transcripts

Browse More Related Video

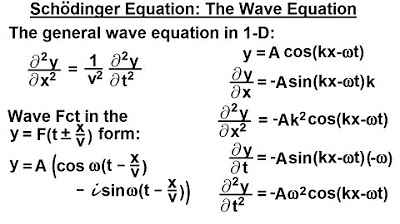
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (3 of 92) The Wave Equation

How Schrodinger Came Up With His Famous Equation (But EASIER)

Lecture 10 | The Theoretical Minimum

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (5 of 92) The Schrodinger Eqn. in 1-D (1/3)

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (6 of 92) The Schrodinger Eqn. in 1-D (2/3)

25. Quantum Mechanics VII: Summary of postulates and special topics

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
QuantumMechanicsWaveEquationsSchrodingerLeapsOfFaithEnergyMomentumdeBrogliePhotonParticleHamiltonianExperimentalValidationTheoreticalPhysics