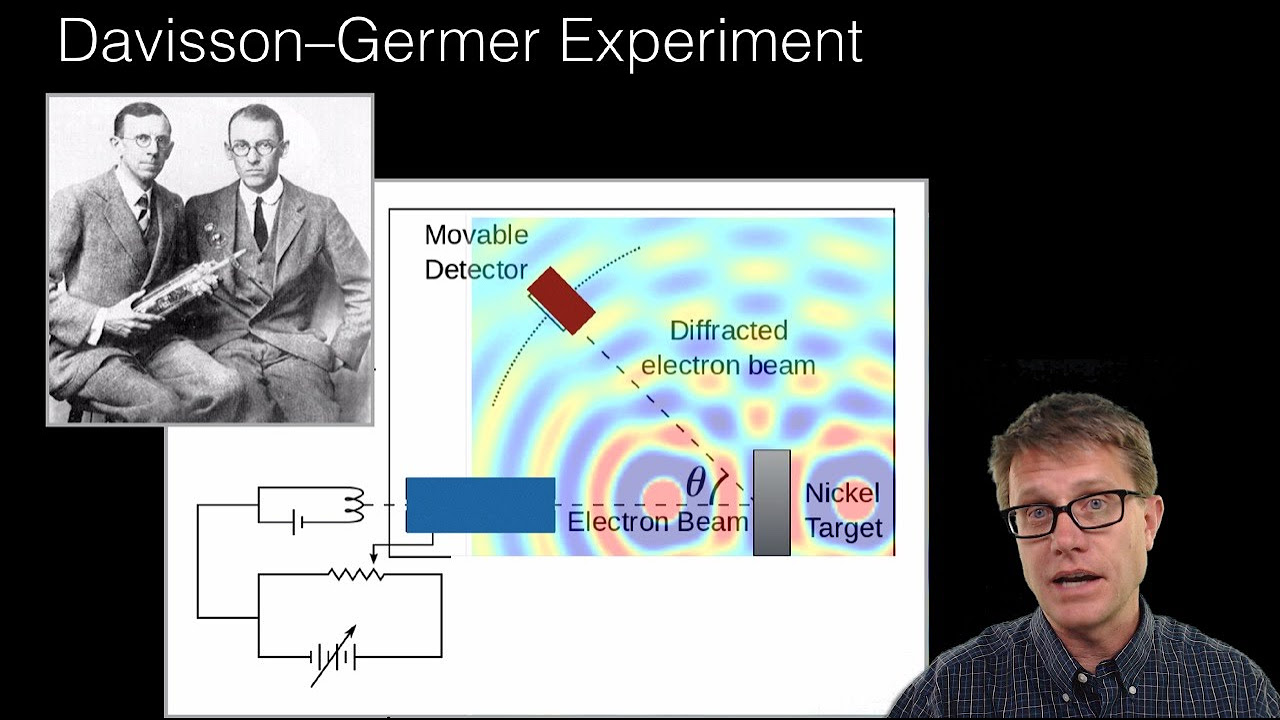
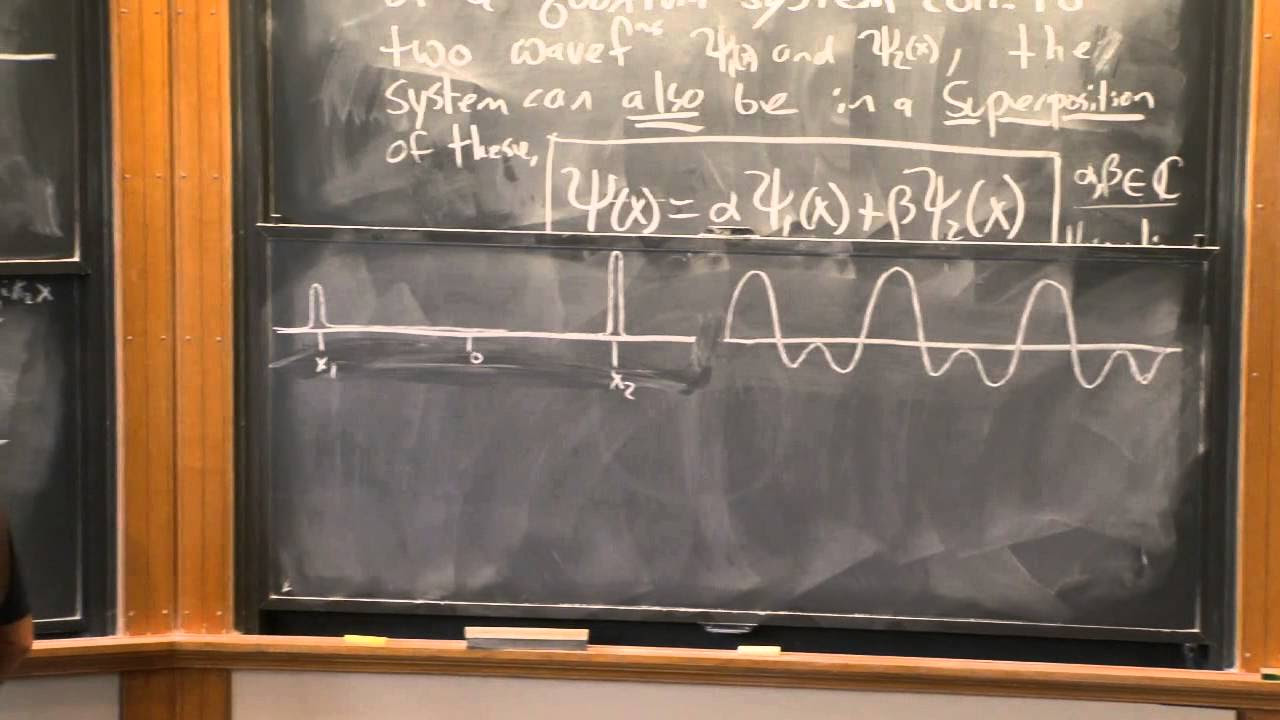Quantum Wavefunction | Quantum physics | Physics | Khan Academy
TLDRThe video explores the concept of wave-particle duality in quantum mechanics, focusing on the wave-like properties of electrons. It explains DeBroglie's hypothesis, Schrodinger's wave function, and Max Born's interpretation of the wave function as a probability density for locating an electron. The script discusses the challenges physicists faced in understanding and interpreting wave functions and highlights ongoing debates about their physical significance. Despite these unresolved issues, the practical application of quantum mechanics continues to yield successful results.
Takeaways
- 🌌 The concept of matter particles like electrons having wavelengths was initially intriguing and led to the development of wave-particle duality.
- 🤔 The challenge of understanding what is 'waving' in an electron's wave-like behavior posed a conceptual puzzle for physicists.
- 📚 Erwin Schrödinger provided the mathematical description of the wave function, which is central to quantum mechanics and is represented by the symbol ψ.
- 🧬 Schrödinger's Equation is crucial for calculating the wave function, involving partial derivatives and Planck's constant, and is fundamental in quantum mechanics.
- 📈 The wave function ψ(x) gives a mathematical shape of the wave at different points in space, which can be visualized graphically.
- 🔮 Schrödinger initially attempted to interpret the wave function as charge density, suggesting the electron's charge is spread out in space.
- 🔄 Max Born later proposed a different interpretation, suggesting the wave function represents the probability of finding an electron at a given point, not its charge density.
- 🎲 Squaring the absolute value of the wave function gives the probability density, which is used to determine where an electron is most likely to be found.
- 🚫 The wave function does not pinpoint the exact location of an electron but provides probabilities based on repeated measurements.
- 🔬 Quantum mechanics allows for progress and practical applications despite differing interpretations of the wave function.
- 💡 The debate on the deeper implications of the wave function continues, but its use in calculating probabilities for measurements is well-established and universally agreed upon.
Q & A
What discovery led to the realization that matter particles like electrons can have wavelengths?
-The discovery by DeBroglie that the wavelength of a matter particle is given by Planck's constant divided by the particle's momentum.
What fundamental question arose when physicists realized that electrons have wavelike properties?
-Physicists wondered what exactly is waving in the case of an electron having a wavelength.
What is a wave function in the context of quantum mechanics?
-A wave function is a mathematical description that provides the shape of the wave associated with a particle, typically represented by the symbol psi (ψ).
Who developed the mathematical description of the wave function?
-Erwin Schrodinger developed the mathematical description of the wave function, known as Schrodinger's Equation.
How did Max Born interpret the wave function differently from Schrodinger?
-Max Born interpreted the wave function as providing the probability of finding the electron at a given point in space, rather than describing the electron's charge density.
What does the square of the wave function represent?
-The square of the wave function represents the probability density of finding the electron at a given point in space.
What issue arises when considering the physical interpretation of the wave function?
-Physicists debate whether the wave function describes a single electron, a system of electrons, or just the measurement of the electron, and how the wave function collapses upon measurement.
What is Schrodinger's Equation used for in quantum mechanics?
-Schrodinger's Equation is used to determine the wave function, which provides the mathematical shape of the wave associated with a particle.
Why do physicists continue to make progress in quantum mechanics despite differing interpretations of the wave function?
-Physicists can use the wave function to obtain probabilities of measurements and make predictions, allowing them to test models and correlate data without needing to fully agree on its interpretation.
What does the wave function tell us about the likelihood of finding an electron in a specific region?
-The wave function indicates regions where the electron is most likely to be found, with higher values corresponding to higher probabilities.
Why might someone still feel unsatisfied with the current understanding of the wave function?
-People might feel unsatisfied because there is no consensus on what the wave function physically represents beyond giving probabilities, and there are unresolved questions about its deeper implications.
Outlines
🔍 Exploring Electron Wave Properties
The concept of electron wavelengths and wave functions is introduced, highlighting the historical context of DeBroglie's contribution. The wave function (psi) provides a mathematical description of an electron's wave properties. Schrodinger's Equation is pivotal in quantum mechanics for deriving this wave function, though its physical interpretation remains complex. Schrodinger suggested the wave function could represent charge density, but this interpretation was later revised by Max Born to denote probability density.
📈 Probability Density and Wave Functions
Max Born's interpretation of the wave function is discussed, emphasizing that the square of the wave function (|psi|^2) gives the probability density of finding an electron in a particular region. The wave function does not determine an exact location but rather a probability distribution. This section explains how different values of psi correlate with the likelihood of detecting electrons in various positions, requiring multiple measurements to establish a consistent pattern.
🤔 Interpreting the Wave Function
The challenges in interpreting the wave function are explored, questioning whether it represents a single electron, a system of electrons, or merely measurement outcomes. The concept of wave function collapse during measurement is introduced. Despite differing interpretations, the practical use of the wave function in predicting probabilities has allowed significant progress in quantum mechanics over the past century. The ongoing debate about the deeper implications of the wave function is acknowledged.
Mindmap
Keywords
💡Wave function
💡Schrodinger's Equation
💡Probability density
💡DeBroglie wavelength
💡Partial derivatives
💡Max Born
💡Charge density
💡Measurement problem
💡Quantum mechanics
💡Planck's constant
Highlights
Matter particles like electrons can exhibit wave-like properties, with a wavelength determined by Planck's constant over momentum.
The concept of what is waving in an electron's wave-like behavior is challenging to understand, unlike physical waves like water or string waves.
Physicists sought a mathematical description and interpretation for the wave of the electron, leading to the development of the wave function.
The wave function, represented by psi (ψ), provides a mathematical shape of the electron's wave at different points in space.
Erwin Schrödinger formulated Schrödinger's Equation, which is fundamental to quantum mechanics and involves the wave function.
Schrödinger's Equation allows for the calculation of the wave function, essential for understanding the electron's wave shape.
Schrödinger initially interpreted the wave function as charge density, suggesting the electron's charge is distributed in space.
Max Born proposed a different interpretation, suggesting the wave function represents the probability of finding an electron at a given point.
The probability of finding an electron is given by the square of the wave function, leading to the concept of probability density.
The wave function does not predict the exact location of an electron but gives the likelihood of finding it in a region.
Experiments must be repeated to verify the wave function's accuracy, as a single measurement is insufficient for confirmation.
Debate persists on the interpretation of the wave function, with questions about its physical reality and implications for single vs. ensemble electrons.
Despite differing interpretations, the practical use of the wave function in calculating probabilities for quantum mechanics continues unabated.
The wave function's deeper implications are still a subject of debate, with no consensus on its physical interpretation.
The act of measuring an electron and the subsequent 'collapse' of the wave function is a topic of ongoing discussion in quantum mechanics.
While interpretations of the wave function are important, practical applications of quantum mechanics have advanced regardless.
The wave function's ability to provide probability densities has been widely accepted, despite debates on its deeper meaning.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: