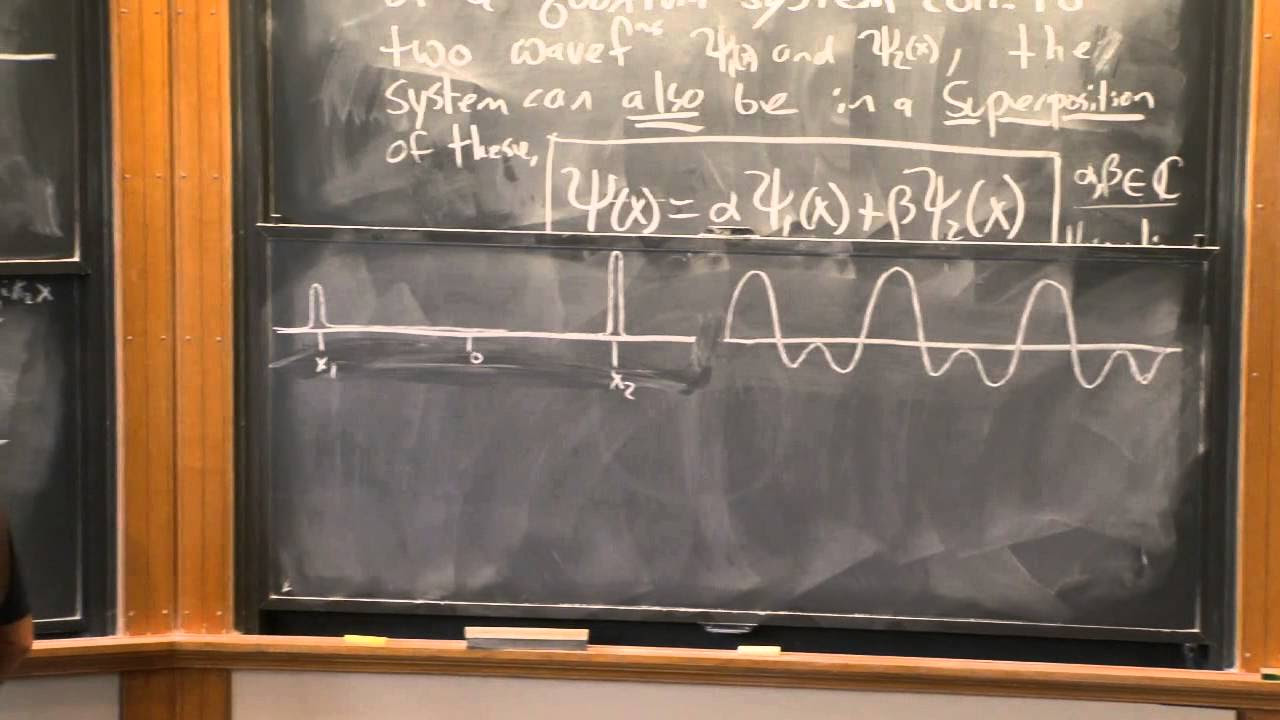Quantum Mechanics and the Schrödinger Equation
TLDRThe video script delves into the quantum mechanics concepts established by Planck, Einstein, and de Broglie, highlighting the wave-particle duality of matter and the quantization of energy. It explains how electrons, due to their small mass, exhibit significant wave-like properties, leading to the concept of standing waves around the atomic nucleus. The script then introduces Schrödinger's equation, which mathematically models quantum systems and introduces the probabilistic nature of electron location, as interpreted by Max Born. The video touches on the philosophical implications of this probabilistic view of nature and mentions various interpretations of quantum mechanics, inviting viewers to further explore the subject.
Takeaways
- 🌟 The Schrödinger equation is a fundamental part of quantum mechanics, developed by Erwin Schrödinger in 1925.
- 📈 Energy quantization and wave-particle duality, established by Planck, Einstein, and de Broglie, are key concepts that underpin the Schrödinger equation.
- 🌊 Electrons exhibit both particle and wave characteristics, with their wavelength being relevant due to their small size.
- 🔄 Electrons in atoms can be viewed as standing waves, with quantization of energy levels arising from the necessity for an integer number of wavelengths.
- 💫 The wave nature of electrons explains phenomena such as covalent bonding through the constructive interference of standing waves.
- 📚 The Hamiltonian operator within the Schrödinger equation describes the total energy and interactions affecting the state of a quantum system.
- 🎲 Max Born's interpretation of the wave function as a probability amplitude is a cornerstone of quantum mechanics, suggesting that the square of the wave function's magnitude represents the probability of an electron's location.
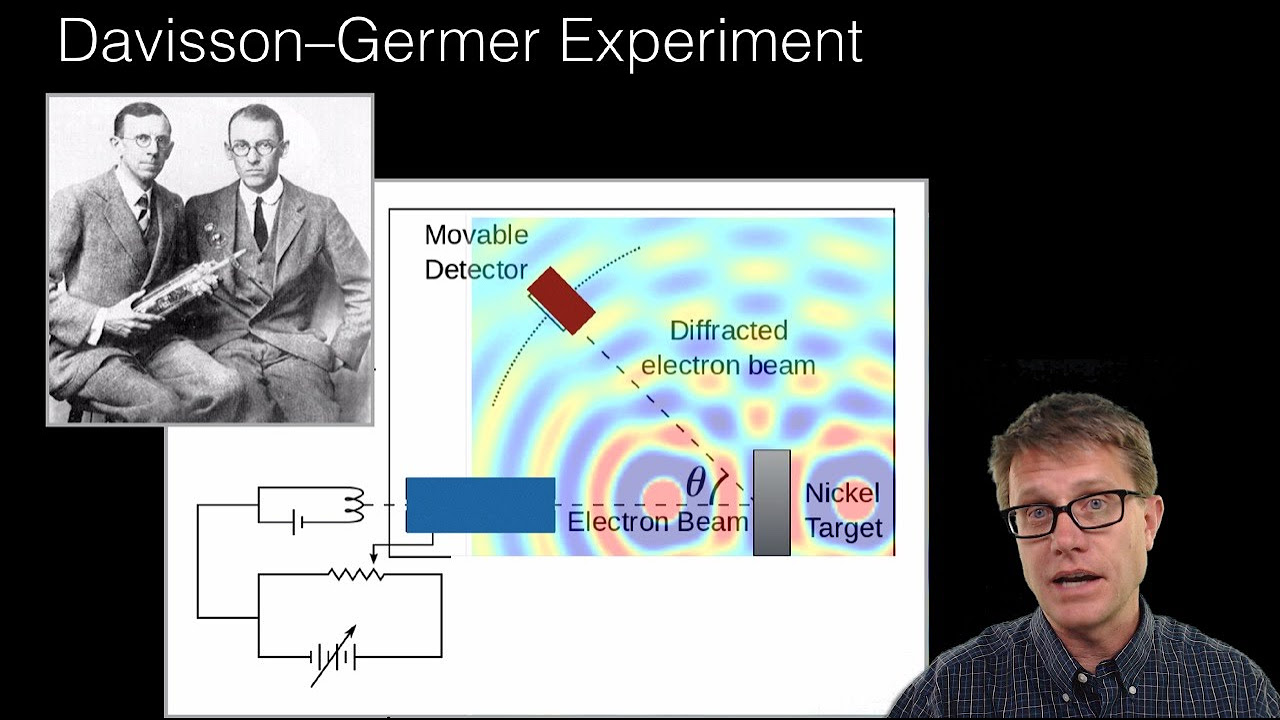
- 🔍 The double-slit experiment illustrates the probabilistic nature of electrons, with the diffraction pattern representing the probability distribution rather than the electrons themselves.
- 🚫 Despite the deterministic nature of the Schrödinger equation, it provides probabilistic information about quantum systems.
- 🌐 Quantum mechanics is not fully understood, with multiple interpretations such as the Copenhagen and many-worlds interpretations still debated among scientists.
- 🔄 The development of quantum mechanics continues with significant contributions from physicists like Werner Heisenberg.
Q & A
What is the significance of the quantization of energy in the context of the Schrodinger equation?
-The quantization of energy is significant because it explains why an electron in an atom can only inhabit discrete energy levels. The circular standing wave representing the electron must have an integer number of wavelengths, which corresponds to quantized energy levels.
How does the wave-particle duality concept relate to the behavior of electrons?
-The wave-particle duality concept indicates that electrons exhibit both particle-like and wave-like properties. This is important for understanding their behavior in quantum systems, such as atoms, where electrons can be viewed as both particles and waves with wavelengths around the size of an atom.
What is the relationship between an object's wavelength and its mass according to de Broglie?
-According to de Broglie, an object's wavelength is inversely proportional to its mass. This means that larger objects have smaller wavelengths, which become negligible for objects much larger than molecules, while smaller objects like electrons have larger wavelengths that are relevant.
How does the Schrodinger equation describe the behavior of quantum systems?
-The Schrodinger equation is a differential equation that describes the wave function of a quantum system, represented by the Greek letter psi. It incorporates the de Broglie relation and mathematical operations known as the Hamiltonian operator, which describes the total energy and interactions affecting the system's state.
What does Max Born's interpretation of the wave function suggest about the nature of quantum systems?
-Max Born proposed that the wave function should be interpreted as a probability amplitude, where the square of the wave function's magnitude describes the probability of finding a particle, like an electron, in a particular location. This suggests that quantum systems exhibit probabilistic behavior rather than deterministic trajectories.
How does the double-slit experiment illustrate the probabilistic nature of electrons?
-In the double-slit experiment, the diffraction pattern observed on a screen is not the path of individual electrons but represents the probability of an electron arriving at each location. This pattern emerges from the collective behavior of many electrons, demonstrating the probabilistic nature of their wave functions.
What is the Hamiltonian operator in the context of the Schrodinger equation?
-The Hamiltonian operator in the Schrodinger equation is a set of mathematical operations that describe all the interactions affecting the state of the quantum system. It can be interpreted as the total energy of the particle, including both kinetic and potential energy.
How does the concept of standing waves relate to the quantization of energy in atomic systems?
-Standing waves, like those proposed for electrons in atoms, require an integer number of wavelengths to exist. This necessity for whole numbers of wavelengths directly leads to the quantization of energy, as each whole number represents a distinct energy level for the electron.
What happens when an electron absorbs a photon of a particular energy?
-When an electron absorbs a photon, its energy increases, promoting the electron to a higher energy state. This change involves an increase in the number of wavelengths within the standing wave, resulting in the electron moving to and occupying a higher energy level.
How does the wave function relate to covalent bonding and orbital overlap?
-The constructive interference of standing waves explains how orbital overlap occurs in covalent bonding. When the wave functions of electrons from different atoms overlap constructively, it results in a lower energy state, which is the basis for the formation of chemical bonds between atoms.
What are some of the different interpretations of quantum mechanics?
-There are several interpretations of quantum mechanics, including the Copenhagen interpretation, the many-worlds interpretation, and others. Each interpretation offers a different perspective on the relationship between the wave function, experimental results, and the nature of reality, but there is no consensus on which is the correct interpretation.
Why was the development of the Schrodinger equation a significant milestone in physics?
-The development of the Schrodinger equation was a significant milestone because it provided a mathematical model that could describe the wave-like behavior of particles, such as electrons, in quantum systems. This equation laid the foundation for our modern understanding of quantum mechanics and has been essential in explaining a wide range of quantum phenomena.
Outlines
🌀 Quantum Concepts and the Schrodinger Equation
This paragraph delves into the foundational concepts of quantum mechanics, highlighting the contributions of Planck, Einstein, and de Broglie. It explains the quantization of energy, the wave-particle duality of light and matter, and the significance of wavelength in relation to mass. The discussion pivots to the wave nature of electrons, describing them as standing waves around the atomic nucleus and explaining the quantization of energy levels. The paragraph further explores the implications of these concepts in chemistry, particularly in covalent bonding. It culminates with the introduction of the Schrodinger equation, its development by Erwin Schrodinger, and its role in describing quantum systems probabilistically.
🌟 Interpretations of Quantum Mechanics and Heisenberg's Role
The second paragraph addresses the probabilistic nature of quantum mechanics and its various interpretations, such as the Copenhagen interpretation and the many-worlds interpretation. It emphasizes the difficulty in accepting the probabilistic foundation of quantum mechanics and introduces the concept of an electron as a cloud of probability density. The paragraph concludes by mentioning Werner Heisenberg and encourages viewers to continue learning about the development of quantum mechanics. Additionally, it provides a call to action for viewers to support the content creator through subscriptions and Patreon.
Mindmap
Keywords
💡Schrodinger equation
💡Quantization
💡Wave-particle duality
💡Standing wave
💡de Broglie relation
💡Hamiltonian operator
Highlights
The Schrodinger equation is a fundamental concept in quantum mechanics.
Energy is quantized, a concept that was established through the work of Planck and Einstein.
Light exhibits wave-particle duality, a concept that was later extended to include matter by de Broglie.
All matter has a wavelength, but for objects larger than a molecule, this wavelength is negligible.
Electrons are small enough that their wavelength is relevant and they exhibit both particle and wave characteristics.
An electron in an atom can be viewed as a circular standing wave surrounding the nucleus.
Quantization of energy applies to electrons because a circular standing wave must have an integer number of wavelengths.
The Bohr model for the hydrogen atom emerges from the concept of standing waves with varying numbers of wavelengths.
Electron excitation occurs when an electron absorbs a photon of particular energy and moves to a higher energy state.
Constructive interference of standing waves explains orbital overlap and covalent bonding in chemistry.
Schrodinger developed the Schrodinger equation in 1925, which incorporated the de Broglie relation.
The Schrodinger equation describes the three-dimensional wave function of a quantum system.
The Hamiltonian operator in the equation describes all interactions affecting the system's state.
Max Born proposed that the wave function should be interpreted as a probability amplitude.
The square of the wave function's magnitude represents the probability of an electron's location.
The double-slit experiment's diffraction pattern illustrates the probability wave of electrons.
The Schrodinger equation provides a deterministic computation of the wave function, but the wave function itself is probabilistic.
Quantum mechanics has various interpretations, including the Copenhagen and many-worlds interpretations.
The development of quantum mechanics will involve consulting Werner Heisenberg's contributions.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: