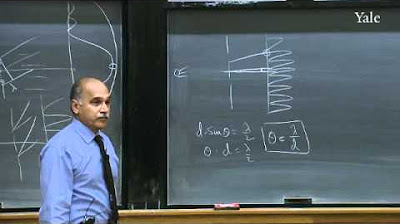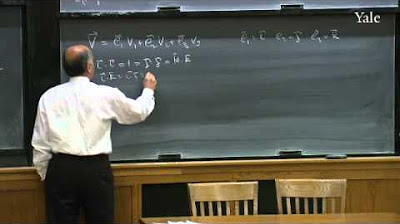Lecture 3: The Wave Function
TLDRThe video script is a transcript of a lecture on quantum mechanics, focusing on the foundational concepts and postulates of the theory. The lecturer introduces the idea that a quantum system's state is fully described by a wave function, a complex-valued function of position. They emphasize the probabilistic nature of quantum mechanics, where the wave function's norm squared at a given point x represents the probability density of finding a particle at that location. The lecture also delves into the superposition principle, which allows for the combination of any two wave functions into a new valid wave function, leading to interference patterns. This principle is central to understanding quantum phenomena. The script also touches on the de Broglie relations, which link the momentum and wavelength of particles, and the Heisenberg uncertainty principle, which imposes limits on the precision with which certain pairs of physical properties, like position and momentum, can be known. The lecturer uses examples and thought experiments to illustrate these concepts, aiming to provide a solid foundation for further study in quantum mechanics.
Takeaways
- 📚 The content provided is under a Creative Commons license and supports MIT OpenCourseWare's mission to offer free, high-quality educational resources.
- 👨🏫 Professor Evans discusses the concept of polarization in the context of quantum mechanics, using polarizers as an analogy to demonstrate the sorting of particles, similar to the behavior of hyper-intelligent monkeys in a theoretical experiment.
- 🧲 The lecture explores the Stern-Gerlach experiment's polarization analogy and its significance in understanding quantum mechanics, including the interference effects.
- ✨ The photoelectric effect is highlighted as evidence that light has both wave-like and particle-like properties, with energy proportional to frequency (Planck's constant) and momentum related to the wavelength.
- ⚛️ De Broglie's hypothesis is introduced, suggesting that all particles, not just light, exhibit both wave and particle characteristics, leading to the concept that every particle has an associated wavelength and frequency.
- 🌟 The Davisson-Germer experiment is mentioned as empirical evidence supporting de Broglie's hypothesis, showing that electrons exhibit both particle and wave properties.
- 📐 Quantum mechanics is presented as a set of rules or postulates for predicting phenomena in the quantum realm, with an emphasis on the importance of these rules being empirically validated.
- 🌱 The wave function (Psi of x) is described as a complete specification of a quantum system's state, being a complex function of position, and every observable property of a particle is encoded in this wave function.
- 🎯 The probability of finding a particle at a certain position is given by the norm squared of the wave function at that position, emphasizing the probabilistic nature of quantum mechanics.
- 🚫 The Heisenberg Uncertainty Principle is alluded to, indicating that one cannot simultaneously know the exact position and momentum of a particle, which is a fundamental concept in quantum mechanics.
- 🤔 The lecture concludes with a demonstration involving the randomness of radioactive decay, illustrating the inherent probability in quantum events and its practical applications, such as random number generation.
Q & A
What is the significance of the polarization analogy in quantum mechanics?
-The polarization analogy is significant in quantum mechanics as it provides a canonical way to understand interference effects. It is a useful tool for visualizing and explaining complex quantum phenomena, particularly the behavior of particles such as electrons in a double-slit experiment.
What is the de Broglie relations?
-The de Broglie relations are fundamental equations in quantum mechanics that relate the momentum of a particle to its wavelength (p = h/λ) and its energy to its frequency (E = hν). These relations suggest that all particles, not just light, can exhibit both wave-like and particle-like properties.
How does the Heisenberg Uncertainty Principle relate to the wave function?
-The Heisenberg Uncertainty Principle states that it is impossible to simultaneously know the exact position and momentum of a particle. In the context of the wave function, this means that the more precisely the position of a particle is known (the wave function is localized in space), the less precisely its momentum can be known (the wave function is spread out in momentum space), and vice versa.
What is the role of the Fourier transform in quantum mechanics?
-The Fourier transform is used in quantum mechanics to switch between the position and momentum representations of a particle's wave function. It allows us to express a particle's wave function as a superposition of plane waves with different wavelengths or, equivalently, different momenta. This is crucial for understanding the wave-particle duality and the uncertainty principle.
Why is the superposition principle important in quantum mechanics?
-The superposition principle is fundamental to quantum mechanics as it allows for the construction of new quantum states from existing ones. It implies that a quantum system can exist in multiple states simultaneously, with each state having its own amplitude and phase. This principle leads to phenomena such as interference and is essential for the probabilistic nature of quantum mechanics.
What is the meaning of the wave function's norm squared?
-The norm squared of the wave function, |ψ(x)|^2, represents the probability density of finding a particle at a certain position x. It is a real, non-negative number that, when integrated over all space, yields the total probability of finding the particle somewhere in the universe, which must equal 1.
How does the wave function provide information about a particle's position and momentum?
-The wave function provides a complete description of a particle's state in quantum mechanics. Its norm squared gives the probability distribution of the particle's position. Additionally, through the de Broglie relations and the Fourier transform, the wave function can provide information about the particle's momentum. However, due to the Heisenberg Uncertainty Principle, the more precisely the position is known, the less precisely the momentum can be known.
What is the significance of the complex numbers in the context of the wave function?
-Complex numbers are used in the wave function to describe the amplitude and phase of a quantum state. The real part of the wave function can be associated with the amplitude of a particle's presence at a particular position, while the imaginary part corresponds to the phase. The complex nature of the wave function allows for the description of interference effects, which are crucial for understanding quantum phenomena.
What is the normalization condition for a wave function?
-The normalization condition for a wave function requires that the integral of the wave function's norm squared over all space is equal to 1. This ensures that the total probability of finding the particle anywhere in the universe sums up to certainty, adhering to the probabilistic nature of quantum mechanics.
How does the interference of wave functions lead to the uncertainty in a particle's position and momentum?
-Interference of wave functions occurs when multiple states are superposed, leading to a probability distribution that can have regions of constructive or destructive interference. This interference pattern becomes more pronounced as more plane waves are superposed, leading to a better-defined position but a less defined momentum, reflecting the Heisenberg Uncertainty Principle.
What is the physical interpretation of the complex conjugate of a wave function in the context of probability amplitudes?
-The complex conjugate of a wave function is used in calculating the probability amplitudes. When multiplied by the original wave function, it results in a real number that represents the probability of a particle being in a particular state. The complex conjugate ensures that the probability is a real and non-negative value, as required by the principles of quantum mechanics.
Outlines
📚 Introduction to Quantum Mechanics and Polarization
The lecture begins with an introduction to the principles of quantum mechanics, emphasizing the importance of understanding the wave function as the complete description of a quantum system. The professor highlights the significance of the Stern-Gerlach experiment and the polarization analogy in grasping quantum phenomena. A live demonstration of polarization with polarizers is conducted to illustrate the concept of electron sorting, drawing parallels with the behavior of light and its interaction with matter.
🌟 The Photoelectric Effect and de Broglie Relations
The discussion shifts to the photoelectric effect, which led to the understanding that light carries energy proportional to its frequency. This concept is extended to the de Broglie relations, suggesting that all particles possess both wave-like and particle-like properties. The lecturer introduces the idea that the momentum of a particle is related to its wavelength, and the energy to its frequency, opening the door to the wave-particle duality.
📈 Quantum States and the Wave Function
The lecturer delves into the specifics of quantum states, asserting that the state of a quantum object is entirely characterized by a wave function, a complex-valued function of position. The audience is guided through understanding the implications of the wave function for a single particle and the challenges of defining a 'not-stupid' wave function that adheres to the principles of quantum mechanics.
🎚️ Probability Density and the Wave Function
The concept of probability density is introduced, stating that the likelihood of finding a particle at a certain position is given by the square of the wave function's magnitude at that position. The lecturer emphasizes the importance of normalization, ensuring that the total probability of finding the particle across all space equals one. The dimensions of the wave function are also discussed, with the audience calculating that it has units of inverse length.
🚩 Position and Momentum Uncertainty
The lecture explores the uncertainty principle, illustrating that a particle's position and momentum cannot both be precisely known at the same time. The wave function's implications for the uncertainty in position and momentum are discussed, with examples provided to show how different wave functions affect these uncertainties. The Fourier transform is introduced as a tool for analyzing wave functions in terms of their momentum space representation.
🤔 The Superposition Principle
The superposition principle is presented as a fundamental aspect of quantum mechanics, allowing for the combination of any two wave functions into a new valid wave function. This principle is exemplified through the creation of superpositions of wave functions corresponding to particles being in different positions, leading to interference patterns and a non-uniform probability distribution that provides partial information about the particle's likely location.
🧲 Experimental Demonstration of Radioactivity
The lecture concludes with a demonstration involving a Geiger counter to highlight the probabilistic nature of radioactive decay. The professor uses an item made from materials containing uranium to show how the clicks of the Geiger counter, indicating radiation detection, occur at seemingly random intervals, underscoring the inherent randomness in quantum phenomena and the suitability of radioactive decay as a source of true randomness.
Mindmap
Keywords
💡Polarization
💡Quantum Mechanics
💡Wave Function
💡Superposition
💡Fourier Transform
💡Uncertainty Principle
💡Probability Density
💡de Broglie Relations
💡Wave-Particle Duality
💡Normalization
💡Complex Numbers
Highlights
The lecture discusses the importance of the polarization analogy in quantum mechanics, emphasizing its usefulness in understanding complex phenomena.
An experiment is conducted to demonstrate the concept of polarization using polarizers, analogous to the sorting behavior of hyper-intelligent monkeys.
The professor illustrates how the orientation of a polarizer can affect the outcome of a polarization experiment, akin to the photoelectric effect.
The concept of wave function is introduced as a complete descriptor of a quantum system's state, replacing the classical need for position and momentum.
The probability density function, derived from the square of the wave function's magnitude, determines the likelihood of finding a particle at a certain position.
Total probability must equal 1, leading to the necessity for wave functions to be normalized.
The dimensions of the wave function are discussed, with emphasis on its importance in understanding quantum mechanics.
Dimensional analysis is highlighted as an essential tool for verifying the correctness of physical equations and calculations.
The superposition principle is introduced, stating that any two valid wave functions can be combined in a superposition, a fundamental concept in quantum mechanics.
Interference effects are explained as a result of adding wave functions and taking the norm squared, leading to probabilities that do not simply add as in classical physics.
The Fourier transform is introduced as a method to express any wave function as a superposition of plane waves with definite momenta.
The Fourier transform coefficients are shown to be equivalent to the wave function in position space, offering a way to determine momentum space probabilities.
The Heisenberg uncertainty principle is alluded to through the trade-off between the localization in position and momentum space.
The lecture concludes with a demonstration of the randomness in radioactive decay, highlighting the probabilistic nature of quantum mechanics.
A real-world application of quantum mechanics is shown through the use of radioactive decay as a random number generator.
The lecture emphasizes the counterintuitive and probabilistic nature of quantum mechanics, distinguishing it from classical physics.
The use of Mathematica for visualizing quantum phenomena, such as the superposition of wave functions, is encouraged for a deeper understanding.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: