Matter as a Wave

Bozeman Science
11 Jul 201505:02
EducationalLearning
32 Likes 10 Comments

TLDRIn this AP Physics essentials video, Mr. Andersen explores the concept of matter as a wave, inspired by Louis de Broglie's hypothesis. De Broglie's wavelength formula, which relates Planck's constant to an object's momentum, explains why we don't perceive everyday objects as waves due to their negligible wavelengths. However, at the quantum level, particles like electrons exhibit wave-like behavior, demonstrated through the interference pattern in the Davvison-Germer experiment. This experiment supports the wave-particle duality of matter, a fundamental principle of quantum mechanics. The video also highlights the practical application of this concept in electron microscopy, which leverages the shorter de Broglie wavelength of electrons for higher resolution imaging compared to visible light.

Takeaways
  • 🌌 Louis de Broglie proposed that matter could behave as a wave, similar to how light can behave as particles.
  • 🔍 De Broglie's wavelength formula is given by Planck’s Constant divided by momentum (mass times velocity).
  • 🚀 The reason we don't observe matter as waves is due to the large mass of objects, which results in a very small wavelength that is not easily observable.
  • 🧲 Scientists Davvison and Germer demonstrated electron interference, showing that electrons can behave as waves.
  • 🔬 Electron microscopes utilize the small de Broglie wavelength of electrons to achieve higher resolution than light microscopes.
  • 🌀 Matter exhibits wave-particle duality, behaving as both a wave and a particle, which is a fundamental concept in quantum mechanics.
  • 🏗️ Classical mechanics applies to large-scale objects, while quantum mechanics is relevant at the nanoscale.
  • 📏 De Broglie's wavelength helps to determine the scale at which classical or quantum mechanics should be applied.
  • 🏌️‍♂️ Applying de Broglie's formula to a baseball shows that its wavelength is extremely small, almost immeasurable.
  • ⚛️ For an electron, the de Broglie wavelength is much larger and comparable to the wavelengths of visible light, allowing for wave-like behavior to be observed.
  • 💥 Wave interference, a phenomenon where waves can constructively or destructively interfere with each other, is not possible with particles alone.
  • 🧐 The Davvison-Germer experiment provided direct evidence of wave-like behavior in electrons through the observation of interference patterns.
Q & A

  • What did Louis de Broglie suggest about the nature of matter?

    -Louis de Broglie suggested that matter might be made of waves, similar to how light is made of particles.

  • What is de Broglie's wavelength formula?

    -De Broglie's wavelength is equal to Planck's Constant divided by momentum, which is mass times velocity.

  • Why don't we typically observe matter as a wave?

    -We don't observe matter as a wave because it has a large mass compared to Planck's constant, resulting in a very small wavelength that is not easily detectable.

  • What experiment demonstrated that electrons can behave like waves?

    -The Davvison-Germer experiment demonstrated electron interference, showing that electrons can behave like waves.

  • How does an electron microscope utilize the wave-like properties of electrons?

    -An electron microscope uses the very small de Broglie wavelength of electrons to achieve higher resolution imaging of objects that are not visible with visible light.

  • What is the concept of wave-particle duality?

    -Wave-particle duality is the concept that all particles, including matter, exhibit both wave-like and particle-like properties.

  • What determines whether we treat matter as a particle or a wave?

    -The scale at which we are observing matter determines whether we treat it as a particle (classical mechanics) or a wave (quantum mechanics).

  • What is the significance of de Broglie's wavelength in determining the scale of observation?

    -De Broglie's wavelength helps determine whether we should observe matter through the lens of classical mechanics (large scale) or quantum mechanics (very small, nanoscopic scale).

  • How does the de Broglie wavelength of a baseball compare to that of an electron?

    -The de Broglie wavelength of a baseball is incredibly small (10^-34), whereas that of an electron is much larger (on the order of 1.2 nanometers), making the wave-like properties of electrons more observable.

  • What is the relationship between the de Broglie wavelength and the resolution of an electron microscope?

    -As the de Broglie wavelength of electrons is close to the wavelengths of visible light in the nanoscopic world, electron microscopes can achieve better resolution than light microscopes.

  • What phenomenon did Davvison and Germer observe in their experiment that confirmed the wave-like behavior of electrons?

    -Davvison and Germer observed interference patterns in the electron beam hitting a nickel target, which confirmed the wave-like behavior of electrons.

Outlines
00:00
🌌 Wave-Particle Duality and de Broglie's Wavelength

This paragraph introduces the concept of wave-particle duality, which is the idea that matter, like light, can exhibit both wave-like and particle-like properties. Louis de Broglie's hypothesis is discussed, suggesting that matter is made of waves and proposing de Broglie's wavelength formula, which is Planck's Constant divided by momentum (mass times velocity). The reason why we don't typically observe matter as a wave is explained by the small mass of particles compared to Planck's constant, resulting in a very small wavelength that is not observable. The paragraph also explains how this concept is applied in electron microscopy, which uses the short de Broglie wavelength of electrons to achieve higher resolution than light microscopes. The scale of observation determines whether classical mechanics or quantum mechanics is more applicable, with de Broglie's wavelength serving as a scale determiner.

Mindmap
Keywords
💡Matter as a wave
The concept of 'matter as a wave' is central to the video's theme, which explores the idea that all matter can exhibit wave-like properties, similar to light's dual nature of being both a particle and a wave. This concept was first proposed by Louis de Broglie and is foundational to quantum mechanics. The video script discusses how this property is not typically observable due to the extremely small wavelengths associated with larger objects, but it becomes significant at the nanoscale.
💡Louis de Broglie
Louis de Broglie was a French physicist who proposed the theory that all matter can exhibit wave-like properties. His work is crucial to the video's narrative as it introduces the concept of de Broglie wavelength, which is a key concept in understanding wave-particle duality. The script mentions de Broglie's hypothesis that matter might be made of waves and how he derived the de Broglie wavelength formula.
💡de Broglie wavelength
The 'de Broglie wavelength' is a formula that calculates the wavelength of a particle based on its momentum. It is given by Planck's constant divided by the product of mass and velocity. In the context of the video, this wavelength is used to determine whether matter behaves more like a wave or a particle, with larger wavelengths indicating more wave-like behavior. The script uses the de Broglie wavelength to illustrate the scale-dependent nature of wave-particle duality.
💡Planck's Constant
Planck's Constant is a fundamental constant in quantum mechanics, denoted by 'h', and it plays a pivotal role in the calculation of the de Broglie wavelength. The script explains that this constant, when divided by an object's momentum, determines the de Broglie wavelength, which in turn affects how we perceive matter—as waves or particles.
💡Wave-particle duality
Wave-particle duality is the concept that every particle or quantum entity can be described as either a particle or a wave, and in some cases, exhibits both properties simultaneously. The video script uses this concept to explain how electrons, for example, can display wave-like interference patterns, which is a key aspect of quantum mechanics and a central theme of the video.
💡Electron microscope
An electron microscope is a type of microscope that uses electrons instead of light to image a sample. The script mentions electron microscopes as an application of the wave-like properties of electrons, where their small de Broglie wavelengths allow for higher resolution imaging than is possible with visible light.
💡Classical mechanics
Classical mechanics is the branch of physics that deals with the motion of macroscopic objects and their interactions under the influence of forces. In the video script, classical mechanics is contrasted with quantum mechanics, with the former being applicable to larger scales where objects behave more like particles.
💡Quantum mechanics
Quantum mechanics is a fundamental theory in physics that describes the physical properties of nature at the scale of atoms and subatomic particles. The script discusses quantum mechanics in the context of treating matter as waves, especially at the nanoscale, where the wave properties of particles like electrons become more apparent.
💡Davvison-Germer experiment
The Davvison-Germer experiment is a historical experiment that demonstrated the wave nature of electrons through the observation of interference patterns. The script describes this experiment as a pivotal moment that confirmed the wave-like behavior of matter, specifically electrons, by observing the interference pattern produced when electrons were scattered off a nickel target.
💡Interference
Interference is a phenomenon where two or more waves superpose to form a resultant wave of greater, lower, or the same amplitude. The script explains that interference is a key property of waves and provides evidence for the wave nature of matter, as demonstrated by the Davvison-Germer experiment where electrons interfered with each other to produce a pattern of varying electron intensity.
💡Momentum
Momentum is the product of an object's mass and velocity and is a key factor in the calculation of the de Broglie wavelength. The script uses momentum to illustrate how the wavelength of matter changes with different masses and velocities, affecting whether we perceive it as a wave or a particle.
Highlights

Louis de Broglie suggested that matter might be made of waves, similar to how light is made of particles.

De Broglie's wavelength formula is Planck’s Constant divided by momentum (mass times velocity).

Matter's large mass makes its wavelength so small it's generally not observable.

Davvison and Germer's experiment demonstrated electron interference, proving wave-like behavior of matter.

Electron microscopes utilize the small de Broglie wavelength of electrons for high-resolution imaging.

Matter exhibits wave-particle duality, behaving as both a wave and a particle.

Classical mechanics treats matter as a particle, while quantum mechanics treats it as a wave.

Scale determines whether classical or quantum mechanics applies, with quantum mechanics relevant at the nanoscopic level.

De Broglie's wavelength serves as a determiner of the applicable physics scale.

Applying de Broglie's formula to a baseball results in an incredibly small wavelength.

The diameter of a hydrogen atom is much larger than the de Broglie wavelength of a baseball.

Electrons have a larger de Broglie wavelength due to their smaller mass and can be treated as waves.

Waves can interfere, which particles cannot, leading to areas of constructive and destructive interference.

Davvison and Germer's experiment sought interference patterns in electrons to confirm their wave nature.

The experiment involved an electron gun, a nickel target, and a movable detector to observe interference.

Data from the experiment showed varying amounts of electric charge at different angles, indicating electron interference.

Understanding the dependence of de Broglie wavelength on mass and velocity is crucial.

The Davvison-Germer experiment confirmed the wave nature of electrons through observed interference.

Transcripts

Browse More Related Video

Matter as a Particle

Are Photons & Electrons Particles or Waves? Make up your mind god!

Quantum Mechanics - Part 2: Crash Course Physics #44

AT&T Archives: Matter Waves, Holden and Germer on Wave Nature and the Davisson-Germer Experiment

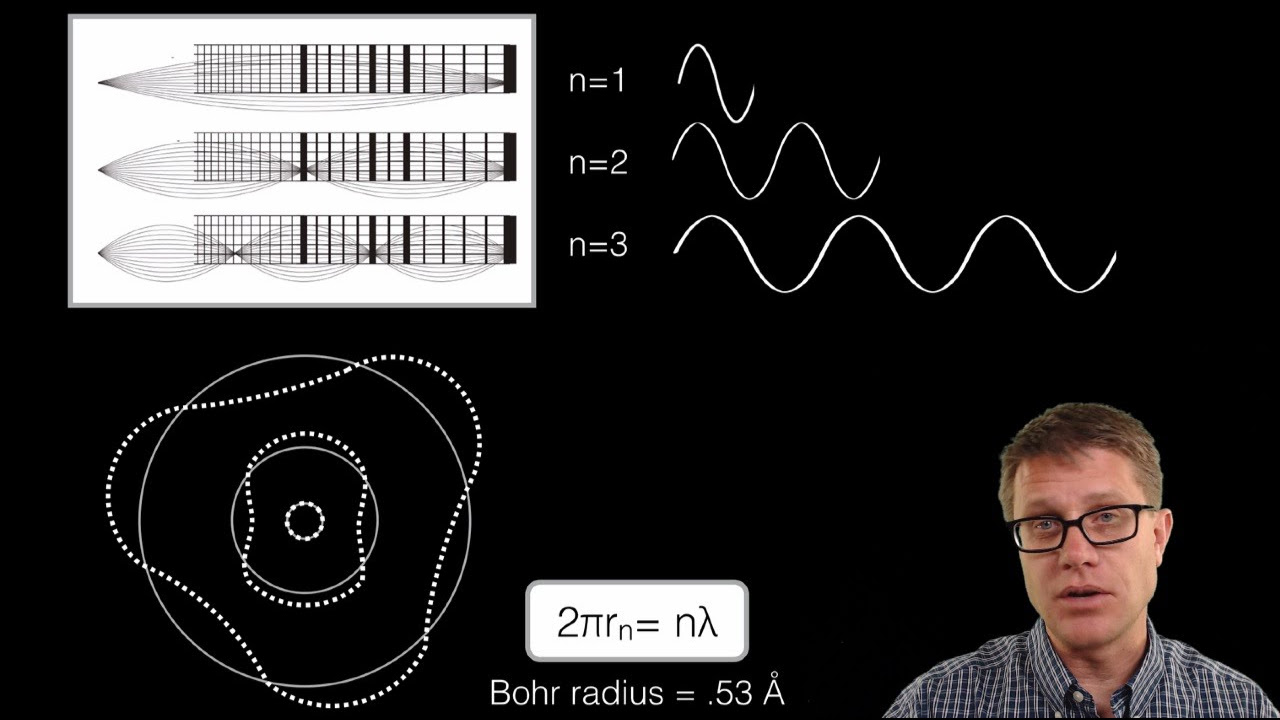
Wave Model of an Electron

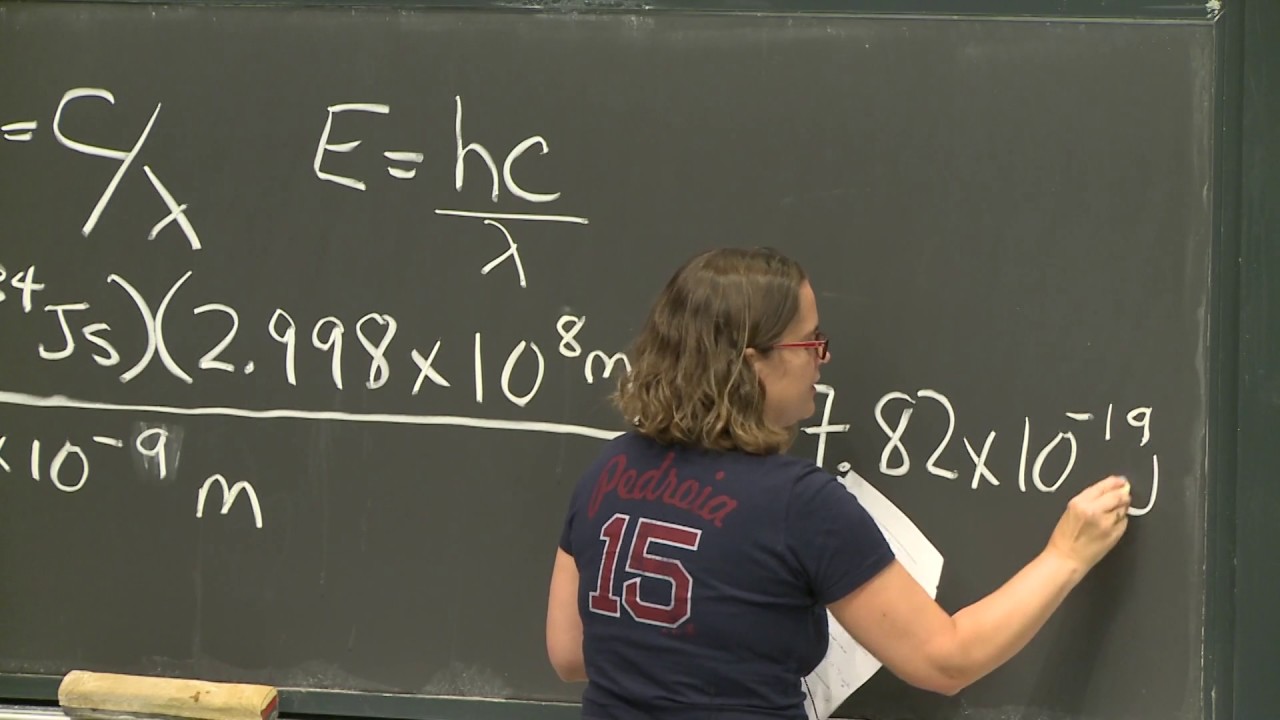
4. Wave-Particle Duality of Matter; Schrödinger Equation

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Wave-Particle Dualityde Broglie WavelengthDavvison-GermerQuantum MechanicsClassical MechanicsElectron MicroscopyMatter WavesInterference PatternPhysics EssentialsAP Physics