Finding Slope of a Polar Curve in Calculus

turksvids
3 Nov 201808:19
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video delves into the calculus of polar curves, focusing on the concept of finding the slope of the tangent to a curve. It emphasizes the importance of converting polar equations to parametric form using x = R*cos(θ) and y = R*sin(θ), and then applying the chain rule to calculate the slope dy/dx. The presenter illustrates the process with examples, including one with trigonometric functions and another without, demonstrating how to evaluate derivatives at specific angles. The video aims to simplify the process by avoiding memorization of formulas and instead understanding the underlying principles, making it accessible for those learning calculus.

Takeaways
  • 📚 The video discusses the calculus of polar curves, focusing on finding the slope of the tangent to the curve.
  • 📐 Polar curves are initially given in the form R = f(θ), which can be any function of θ, such as R = cos(7θ) or R = 1 + 2sin(θ).
  • 🔄 To work with polar curves, they are converted into parametric equations using x = Rcos(θ) and y = Rsin(θ).
  • 📈 The slope of the tangent to a polar curve is found using the chain rule, specifically dy/dθ divided by dx/dθ.
  • 🚫 The video emphasizes not to just memorize formulas but to understand the concept of using the chain rule for these calculations.
  • 📝 An example is given with R = cos(2θ), and the slope is calculated at θ = π/3, illustrating the process step by step.
  • 📉 The slope of a polar curve is still represented as dy/dx, even though the curve is in the polar coordinate system.
  • 🔢 The importance of knowing the values of trigonometric functions on the unit circle is highlighted for evaluating derivatives.
  • 📌 The video demonstrates the calculation of dx/dθ and dy/dθ for the example R = cos(2θ), including the application of the product rule and chain rule.
  • 📊 The final slope for the example R = cos(2θ) at θ = π/3 is simplified to 7/√3, which is confirmed using a calculator.
  • 🤔 A second example is presented where R = θ²/2, and the process is repeated for θ = π/2, showing how to handle cases without trigonometric functions in the definition of R.
  • 🔍 The video concludes by reiterating the importance of understanding the process rather than just memorizing formulas, and wishes the viewers good luck.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is the calculus of polar curves, specifically finding the slope of the tangent to the curve.

  • What is the starting point for converting a polar curve to a parametric equation?

    -The starting point is given by an equation of the form R = f(θ), where R is a function of the angle θ.

  • How can a polar curve be converted into a parametric equation in terms of x and y?

    -A polar curve can be converted into a parametric equation using x = R * cos(θ) and y = R * sin(θ).

  • What is the formula used to calculate the slope of a curve in terms of parametric equations?

    -The slope of a curve is calculated using dy/dθ divided by dx/dθ, which is derived from the chain rule.

  • Why is it important to remember the conversion formulas for x and y in terms of R and θ?

    -It is important because these formulas are frequently used in the process of finding the slope of a polar curve.

  • What is the example polar curve given in the video?

    -The example polar curve given is R = cosine(2θ).

  • At what angle is the slope of the example curve calculated in the video?

    -The slope is calculated at θ = π/3.

  • What is the significance of the unit circle in evaluating trigonometric functions at specific angles?

    -The unit circle provides the values of sine and cosine for standard angles, which are crucial for simplifying expressions when evaluating derivatives.

  • How does the video demonstrate the calculation of dx/dθ for the example curve?

    -The video uses the product rule and the chain rule to find the derivative of x with respect to θ, and then evaluates it at θ = π/3.

  • What is the final result for the slope of the example curve at θ = π/3?

    -The final result for the slope is 7/√3.

  • What is the second example given in the video, and how does it differ from the first?

    -The second example is R = θ²/2, evaluated at θ = π/2. It differs from the first because there are no trigonometric functions in the definition of R.

  • How does the video handle the absence of trigonometric functions in the second example?

    -The video still applies the product rule to find derivatives and evaluates them at the given angle, using the properties of the unit circle where applicable.

  • What is the final result for the slope of the second example curve at θ = π/2?

    -The final result for the slope is -4/π.

Outlines
00:00
📚 Introduction to Calculus of Polar Curves

This paragraph introduces the topic of the calculus of polar curves, focusing on finding the slope of the tangent to the curve. The speaker emphasizes the importance of converting polar equations to parametric equations using x = R * cos(θ) and y = R * sin(θ). The concept of using the chain rule to calculate the slope dy/dx is introduced, and the speaker advises against memorizing formulas, instead suggesting understanding the underlying principles. An example is presented where R = cos(2θ), and the process of finding the slope at θ = π/3 is explained step by step, including the use of the unit circle and trigonometric identities.

05:00
🔍 Detailed Calculation of Slope for Polar Curves

The second paragraph delves deeper into the calculation process, using the example of R = θ^2 / 2 at θ = π/2. The speaker demonstrates the application of the product rule to find derivatives dx/dθ and dy/dθ, and then evaluates these at the given angle. The paragraph highlights the importance of knowing values from the unit circle for accurate substitution. The slope dy/dx is found by dividing dy/dθ by dx/dθ, resulting in a unique slope for the curve at the specified angle. The speaker also shares a screenshot of using a calculator to verify the results, emphasizing the utility of technology in checking manual calculations.

Mindmap
Keywords
💡Calculus of Polar Curves
Calculus of polar curves is a branch of calculus that deals with the analysis of curves represented in polar coordinates. In the video, this concept is central to understanding how to find the slope of the tangent to a curve. The script discusses converting polar equations to parametric equations to facilitate this analysis, which is essential for students learning differential calculus.
💡Polar Curve
A polar curve is a graphical representation of a mathematical relationship between two variables, r and θ, where r is the radius and θ is the angle in polar coordinates. In the video, the script uses examples like R = cosine(2θ) to illustrate how to find the slope of the tangent line at a specific point on the curve.
💡Parametric Equation
Parametric equations are a way to express the coordinates of a point as functions of a third variable, typically denoted as 't'. In the context of the video, the script explains converting a polar curve to parametric form using x = R * cos(θ) and y = R * sin(θ), which is crucial for applying calculus techniques to find the slope of the tangent line.
💡Chain Rule
The chain rule is a fundamental principle in calculus used to compute the derivative of a composite function. The video script emphasizes the importance of the chain rule when calculating the derivative of the parametric equations derived from a polar curve, as it allows for finding the slope dy/dx.
💡Slope of the Tangent
The slope of the tangent to a curve at a given point is a measure of the steepness of the curve at that point. In the video, the script demonstrates how to calculate this slope for a polar curve by finding dy/dx, which is a key concept in differential calculus and is illustrated through specific examples.
💡Product Rule
The product rule is a derivative rule in calculus that is used when differentiating a product of two functions. The script applies the product rule when finding dx/dθ and dy/dθ from the parametric equations, which is a necessary step in determining the slope of the tangent to a polar curve.
💡Unit Circle
The unit circle is a circle with a radius of one, centered at the origin, and is used in trigonometry to define the sine and cosine functions. The video script mentions the importance of knowing the values of trigonometric functions on the unit circle, especially for angles like π/3 and π/2, which are used in evaluating the derivatives at specific points.
💡Derivative
In calculus, a derivative represents the rate at which a function changes with respect to its variable. The script discusses finding the derivatives dx/dθ and dy/dθ, which are essential for calculating the slope of the tangent to a polar curve.
💡Trigonometric Functions
Trigonometric functions, such as sine and cosine, are mathematical functions of an angle. In the video, trigonometric functions are used within the context of polar curves and their derivatives, as seen in the examples where cosine(2θ) and sine(θ) are part of the expressions being differentiated.
💡Rationalize
Rationalizing a denominator is the process of eliminating square roots or other irrational numbers from the denominator of a fraction. The script mentions that calculators often automatically rationalize results, but when doing calculations by hand, the instructor chooses not to rationalize, leaving the slope in its simplest form.
💡Example Problems
Example problems are used in educational content to illustrate how to apply concepts or solve for specific values. The video script provides detailed example problems involving polar curves and their derivatives, which help viewers understand the process of finding the slope of the tangent line at a given point on a polar curve.
Highlights

Introduction to the calculus of polar curves and the concept of finding the slope of the tangent to a curve.

Explanation of converting polar curves to parametric equations using x = R * cos(θ) and y = R * sin(θ).

Importance of remembering the conversion formulas for x and y in polar coordinates.

Calculation of the slope dy/dx using the chain rule and the derivatives dy/dθ and dx/dθ.

Emphasis on understanding the chain rule rather than memorizing formulas for polar curve calculus.

Example problem: Finding the slope of the curve R = cos(2θ) at θ = π/3.

Use of the product rule to find dx/dθ for the given polar curve example.

Evaluation of derivatives at θ = π/3 using values from the unit circle.

Substitution of values and simplification to find dx/dθ for the example.

Finding dy/dθ using the product rule and evaluating at θ = π/3 for the example.

Simplification of dy/dθ and preparation for calculating the slope dy/dx.

Final calculation of the slope dy/dx for the example using the derived values of dy/dθ and dx/dθ.

Verification of the calculated slope using a calculator for accuracy.

Introduction of a second example with R = θ^2 / 2 and θ = π/2.

Application of the product rule to find dx/dθ for the second example without trigonometric functions.

Evaluation of the derivatives at θ = π/2 and simplification for the second example.

Calculation of dy/dθ for the second example and its simplification.

Final calculation of the slope dy/dx for the second example and its interpretation.

Use of a calculator to verify the results of the second example and the importance of understanding the unit circle values.

Conclusion and summary of the process for finding the slope of polar curves and the importance of practice.

Transcripts

Browse More Related Video

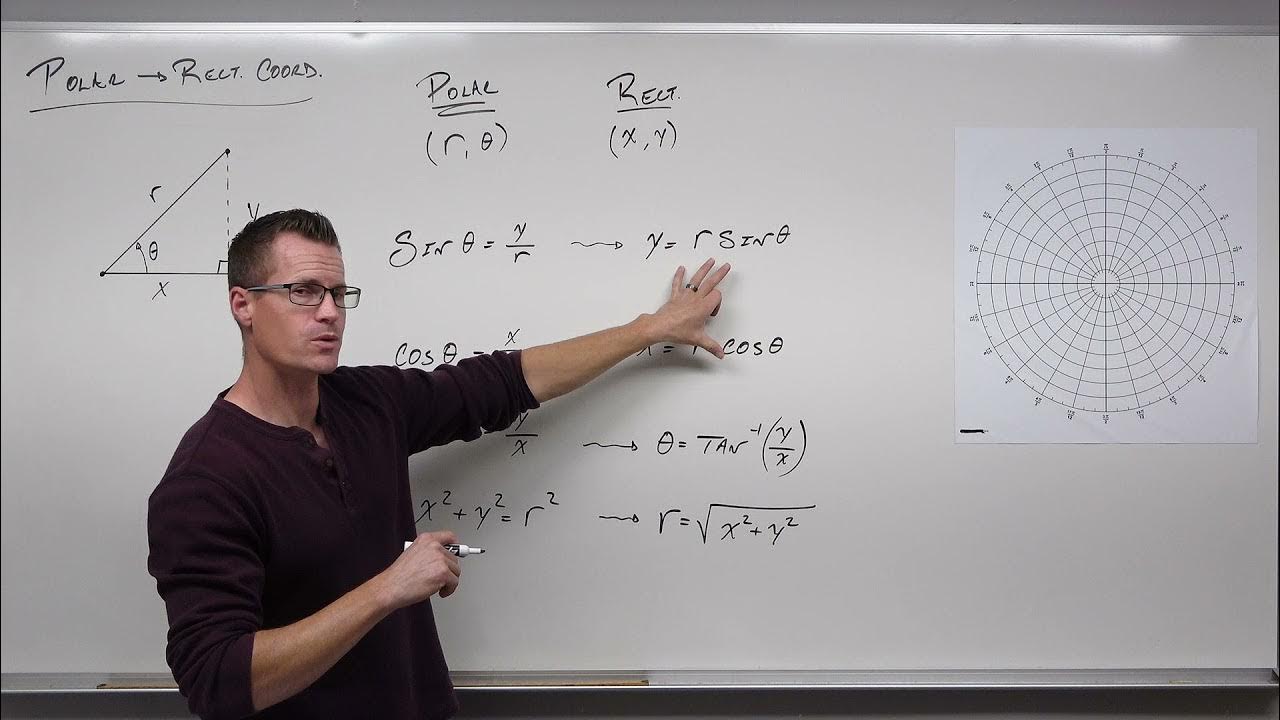
How to Convert From Polar Coordinates to Rectangular Coordinates (Precalculus - Trigonometry 37)

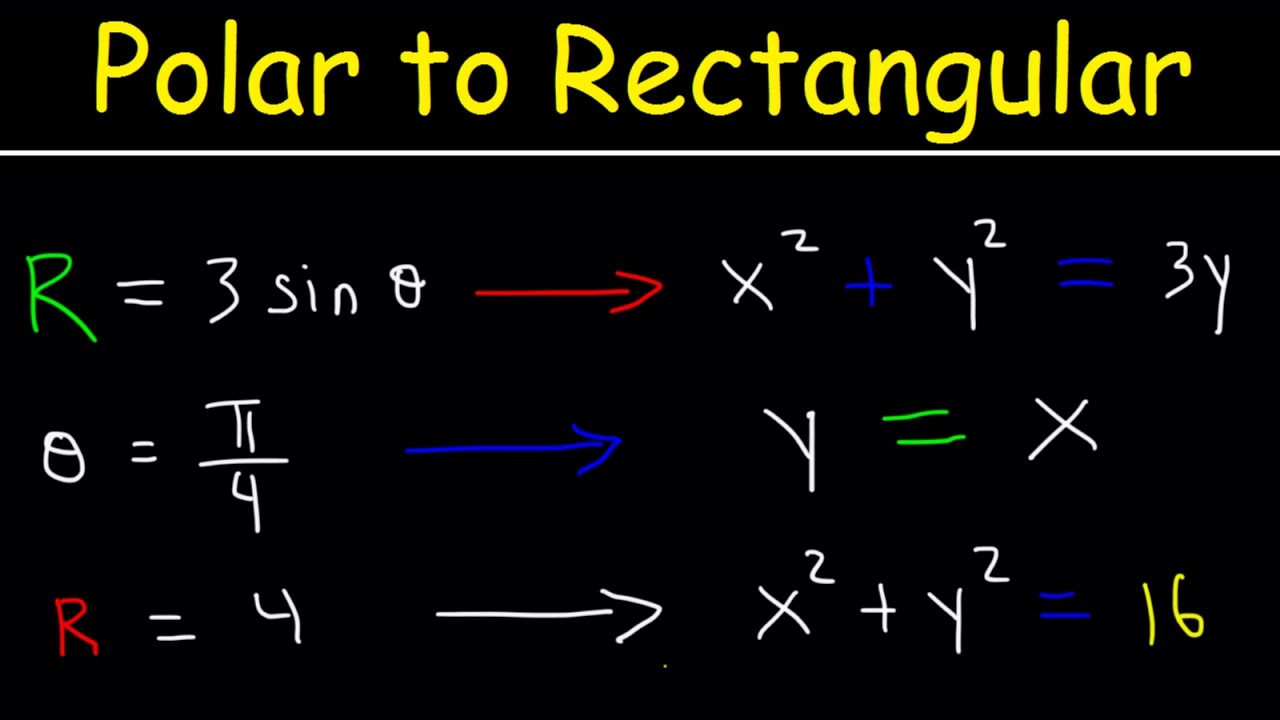
Polar Equations to Rectangular Equations, Precalculus, Examples and Practice Problems

Polar coordinates 3 | Parametric equations and polar coordinates | Precalculus | Khan Academy

How To Graph Polar Equations

How to Convert From Rectangular Equations to Polar Equations (Precalculus - Trigonometry 39)

Notes on Polar, Day 3

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Polar CurvesCalculusParametricTangent SlopeTrigonometryChain RuleUnit CircleSine FunctionCosine FunctionMath Tutorial