How to Convert From Rectangular Equations to Polar Equations (Precalculus - Trigonometry 39)
TLDRThe video script offers an insightful tutorial on converting equations from rectangular to polar coordinates. It emphasizes the utility of polar equations for graphing shapes like circles and ellipses, which may not be functions, and are more easily represented in polar form. The process involves identifying and replacing 'x^2 + y^2' with 'r^2' and substituting 'x' with 'r*cos(θ)' and 'y' with 'r*sin(θ)' for remaining terms. The script walks through several examples, illustrating how to simplify the equations and when it's permissible to divide by 'r'. It also touches on the representation of vertical, horizontal, and diagonal lines in polar coordinates. The tutorial is practical, guiding viewers on when and how to simplify polar equations for clearer understanding and easier graphing.
Takeaways
- 📐 **Conversion Process**: To convert from rectangular to polar equations, replace x^2 + y^2 with r^2 and substitute x with r*cos(θ) and y with r*sin(θ).
- 🔍 **Identifying Patterns**: Look for the pattern x^2 + y^2 in rectangular equations, which directly translates to r^2 in polar equations.
- ⚙️ **Simplifying Equations**: After converting to polar form, simplify the equation as much as possible, considering whether r=0 is a valid solution.
- 🧮 **Graphing Advantages**: Polar equations are advantageous for graphing circles, ellipses, and other curves that are not functions, as opposed to rectangular coordinates which are better for straight lines and simple functions.
- 📈 **Solving for r**: When possible, solve the polar equation for r to simplify the equation and make it easier to understand and graph.
- 🚫 **Excluding r=0**: In some cases, the solution r=0 may be excluded to avoid the pole, which represents a single point at the center.
- 🔄 **Using Identities**: Utilize trigonometric identities, such as double angle formulas, to simplify polar equations further.
- 🤔 **Considering Context**: The choice to convert or not depends on the context; some equations may be simpler to work with in rectangular form, while others are more intuitive in polar form.
- 📉 **Graphing Linear Equations**: Even linear equations like vertical, horizontal, or diagonal lines can be converted into polar form, although they may not always be simpler.
- 🤓 **Advanced Conversions**: For more complex conversions, such as distributing and factoring, it's important to be cautious of the potential loss of solutions and domain restrictions.
- ⏲ **Upcoming Topic**: The next video will cover converting polar equations back into rectangular form, providing a full understanding of the conversion process.
Q & A
What is the main topic of the video?
-The main topic of the video is converting equations from rectangular coordinates (x's and y's) to polar coordinates (r's and thetas).
Why might one want to convert rectangular equations to polar equations?
-One might want to convert rectangular equations to polar equations because certain shapes like circles, ellipses, and cardioids are easier to graph using polar coordinates.
What is the first step in converting a rectangular equation to a polar equation?
-The first step is to look for terms that can be combined to form x squared plus y squared and replace that with r squared.
What is the significance of the Pythagorean theorem in converting rectangular equations to polar equations?
-The Pythagorean theorem is significant because it provides the relationship between x squared plus y squared and r squared in polar coordinates, which is a key step in the conversion process.
What is the general rule for replacing x and y with polar coordinates?
-The general rule is to replace x with r cosine theta and y with r sine theta when converting to polar coordinates.
What is the shape represented by the equation r equals square root of 6 over 2?
-The shape represented by the equation r equals square root of 6 over 2 is a circle with a radius of exactly square root of 6 over 2, centered at the pole.
Why is it sometimes acceptable to exclude r equals zero when converting equations?
-It is sometimes acceptable to exclude r equals zero because it represents a point at the pole with a radius of zero, which is often just a single point and not a continuous shape or function.
What happens if you can't factor x squared plus y squared from the rectangular equation?
-If you can't factor x squared plus y squared, you revert to using the individual variable replacements: x with r cosine theta and y with r sine theta.
What is the identity used in the conversion of the equation 2xy equals 1 to polar form?
-The identity used is the double angle identity for sine, where 2 sine theta cosine theta equals sine 2 theta.
How does the process of converting rectangular equations to polar differ for lines compared to circles or ellipses?
-For lines, especially vertical, horizontal, or diagonal lines, the conversion to polar form may not be necessary as they are often simpler to graph in rectangular coordinates. However, if needed, x is replaced with r cosine theta and y with r sine theta, and then solved for r if possible.
What is the final step in converting a rectangular equation to a polar equation?
-The final step is to simplify the equation as much as necessary, which may include factoring r out, dividing by r if r equals zero is not a solution, or using trigonometric identities to express the equation in terms of sine and cosine.
Outlines
📚 Introduction to Polar Coordinates
The video begins with an introduction to converting equations from rectangular to polar coordinates. The presenter explains the difference between rectangular equations, which are graphed on an x-y coordinate plane, and polar equations, which are graphed on a polar coordinate system with a polar axis and a pole (origin). The conversion process is outlined, emphasizing the substitution of x^2 + y^2 with r^2 as a key step. The video promises to go in-depth on the topic, with examples to illustrate the conversion process.
🔍 Converting Equations: Circles and Ellipses
The presenter discusses why converting to polar coordinates is beneficial, particularly for shapes like circles and ellipses that are not functions. They provide a step-by-step guide on converting the equation 2x^2 + 2y^2 = 3 into a polar equation, resulting in r = √6/2. The explanation highlights that r represents a constant distance from the pole, and the equation describes a circle with a fixed radius around the pole, regardless of the angle θ.
📐 Advanced Conversion Techniques
The video continues with advanced conversion techniques, focusing on equations that do not have an x^2 + y^2 term. The presenter demonstrates how to revert to individual variables and substitute x with r*cos(θ) and y with r*sin(θ). They also cover scenarios where dividing by r is not allowed, and how to handle such cases by factoring and applying the zero product property to obtain multiple equations. The process is illustrated using the equation x^2 = 4y.
🤔 Dealing with Functions and Simplification
The presenter addresses how to convert and simplify equations like 2xy = 1, which do not have an x^2 + y^2 term, by substituting x and y with their polar equivalents. They caution against dividing by r when r=0 is not excluded, as it may lead to loss of solutions. The video also explores the use of trigonometric identities to simplify the equation further, resulting in r^2 * sin(2θ) = 1.
🧮 Complex Equations and Factoring
The video script delves into handling more complex equations like x - 3)^2 + y^2 = 9. The presenter shows how to distribute and group terms to create an r^2 term, then factor out r to simplify the equation to r = 6*cos(θ). They emphasize the importance of being cautious with solutions, especially when r=0 is a possibility, and how different textbooks may treat this solution differently.
📐 Rectangular vs Polar for Lines
The presenter contrasts the ease of graphing certain types of equations in rectangular coordinates versus polar coordinates. They provide examples of vertical, horizontal, and diagonal lines in rectangular form and show how they can be converted into polar form. The video emphasizes that while some equations, like lines and conic sections, may be simpler to graph in rectangular coordinates, others may benefit from conversion to polar form.
🔄 Converting Back and Forth
The video concludes with a teaser for the next video, where the presenter promises to discuss converting polar equations back into rectangular form. They summarize the importance of understanding when and how to use polar coordinates, and how to simplify equations using trigonometric identities and factoring techniques.
Mindmap
Keywords
💡Rectangular Equations
💡Polar Equations
💡Conversion
💡Pythagorean Theorem
💡Circle
💡Ellipse
💡Cardioid
💡
💡Factoring
💡Graphing
💡Conic Sections
💡Sine and Cosine Functions
Highlights
The video teaches the conversion of equations from rectangular to polar coordinates.
Rectangular equations are represented using x's and y's, while polar equations use r's and thetas.
Polar equations are useful for graphing circles, ellipses, and other curves that are not functions.
The conversion process involves replacing x^2 + y^2 with r^2 and substituting x and y with r*cos(θ) and r*sin(θ), respectively.
The video provides a step-by-step guide to converting equations, including factoring and using the Pythagorean theorem.
An example is given where 2x^2 + 2y^2 = 3 is converted to a polar equation, resulting in r = sqrt(6)/2.
The meaning of r in polar equations is explained as the distance from the pole (origin) to the point on the curve.
The video demonstrates that the conversion can simplify the representation of shapes like circles.
The process of converting points from rectangular to polar is discussed, emphasizing the infinite collection of points that define a function or curve.
The video cautions about dividing by r in polar equations, as it can lead to loss of solutions or domain issues.
Alternative methods for simplifying polar equations are presented, including using trigonometric identities.
The video includes examples of converting various types of equations, such as parabolas and lines, into polar form.
The conversion of vertical, horizontal, and diagonal lines to polar equations is demonstrated, showing different approaches based on the context.
The importance of understanding when to use rectangular or polar coordinates for graphing is emphasized.
The video concludes with a teaser for the next video, which will cover converting polar equations back to rectangular form.
Throughout the video, the presenter uses humor and relatable analogies to make complex mathematical concepts more accessible.
The video is designed to provide a deep understanding of the conversion process, not just the mechanical steps.
Transcripts
Browse More Related Video

Polar coordinates 3 | Parametric equations and polar coordinates | Precalculus | Khan Academy
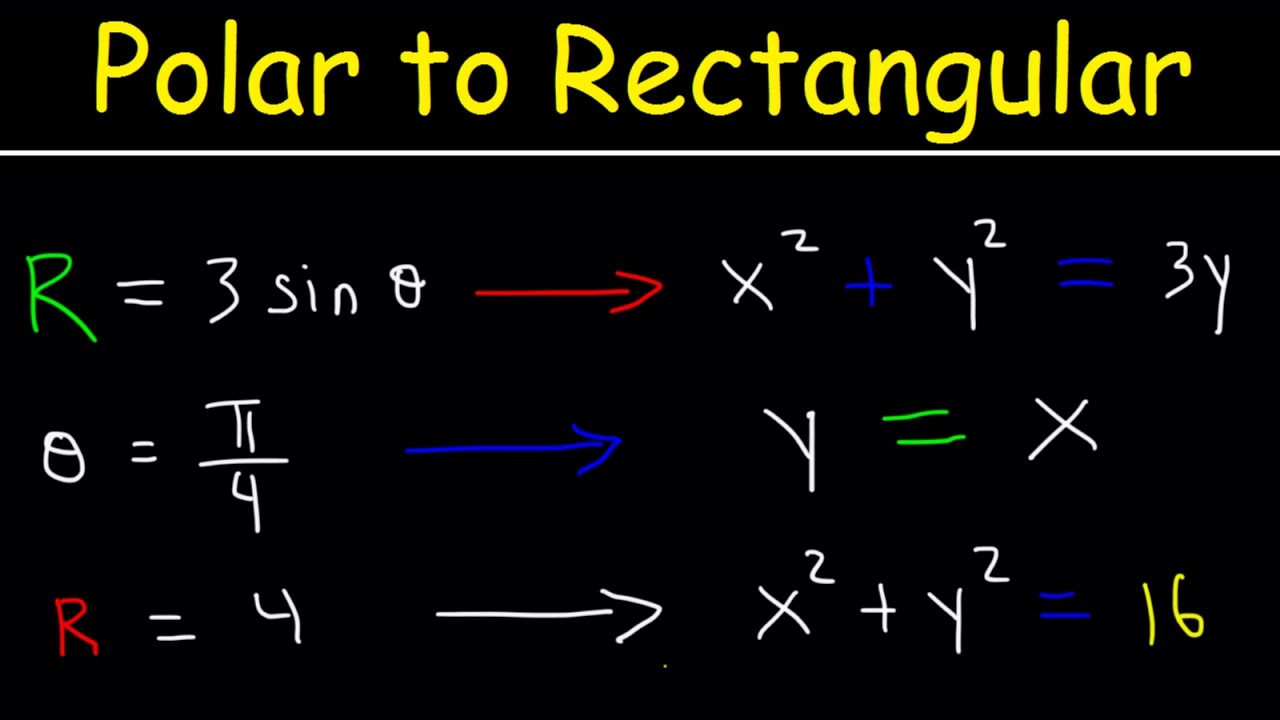
Polar Equations to Rectangular Equations, Precalculus, Examples and Practice Problems

Polar coordinates 2 | Parametric equations and polar coordinates | Precalculus | Khan Academy
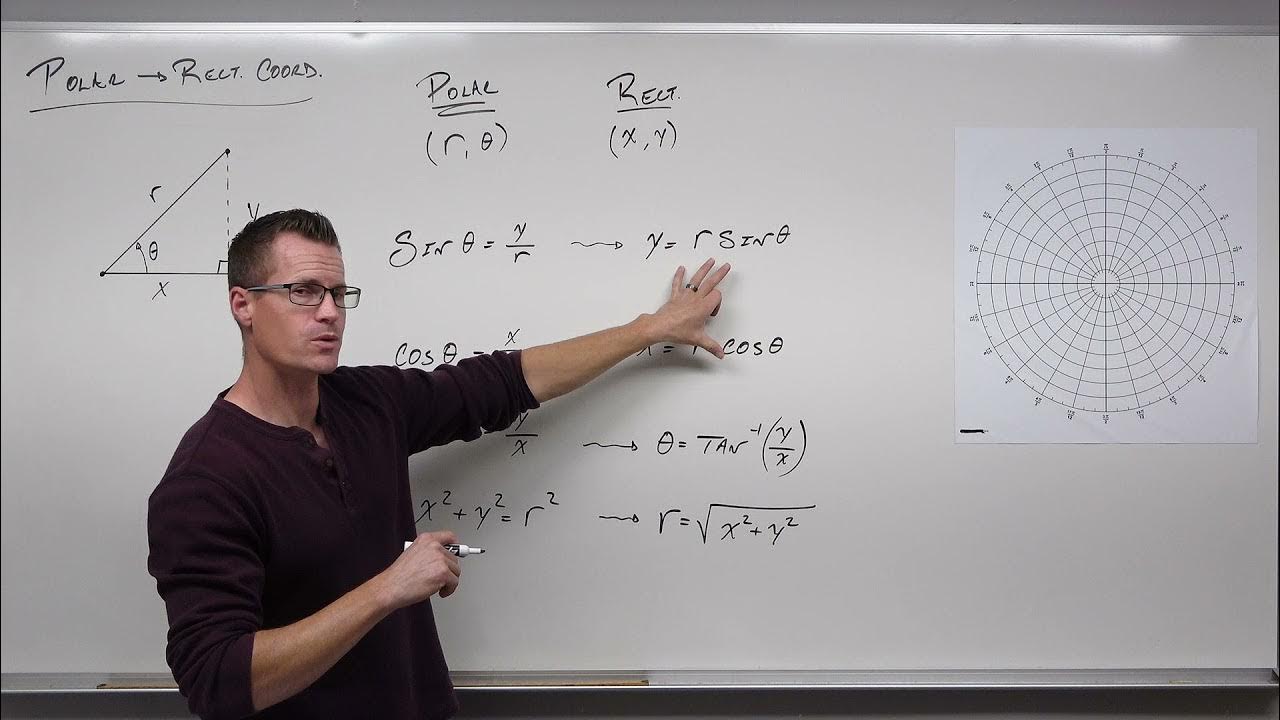
How to Convert From Polar Coordinates to Rectangular Coordinates (Precalculus - Trigonometry 37)

How To Graph Polar Equations

Rectangular Equation to Polar Equations, Precalculus, Examples and Practice Problems
5.0 / 5 (0 votes)
Thanks for rating: