Polar Equations to Rectangular Equations, Precalculus, Examples and Practice Problems
TLDRThis video script offers a comprehensive guide on converting polar equations to rectangular equations, which is essential for understanding coordinate systems and their transformations. The script begins by introducing key formulas relating to the right triangle where x and y are the sides, r is the hypotenuse, and θ (theta) is the angle. It explains that x^2 + y^2 = r^2, x = r cos θ, y = r sin θ, and tan θ = y/x are fundamental in this conversion process. The script distinguishes polar equations, which involve r and θ, from rectangular equations, which use x and y variables. It then walks through various examples, demonstrating how to manipulate and simplify polar equations to their rectangular counterparts using algebraic techniques and trigonometric identities, such as the double angle formula. The examples cover a range of scenarios, from simple constant r values to more complex expressions involving trigonometric functions and their inverses. The script concludes with a problem involving the conversion of an equation with a cosine squared term, illustrating the process of squaring both sides, expanding, and simplifying to obtain the final rectangular form. This summary encapsulates the video's educational content, highlighting its utility for those studying mathematics and seeking to master the conversion between polar and rectangular equations.
Takeaways
- 📚 Converting a polar equation to a rectangular equation involves using formulas relating r, x, y, and θ (r = x^2 + y^2, x = r*cos(θ), y = r*sin(θ), and tan(θ) = y/x).
- 🔍 Polar equations include variables r and θ, while rectangular equations use x and y.
- 📉 To convert r = 7 (a polar equation) to rectangular form, square both sides to get x^2 + y^2 = 49.
- 📈 If θ = π/4, multiplying both sides of tan(θ) = tan(π/4) by x results in y = x.
- ✂️ For θ = 0°, multiplying both sides by x leads to y = 0, since tan(0) = 0.
- 🚫 When θ = π/2, tan(θ) is undefined, implying x must be 0 since division by zero is undefined.
- 🔄 Replacing r*sin(θ) with y and r*cos(θ) with x directly gives the rectangular form for equations like r*sin(θ) = 5 and r*cos(θ) = 4.
- 🔄 For r = 3*cosec(θ), multiplying both sides by sin(θ) and using y = r*sin(θ) results in y = 3.
- 🔄 Similarly, for r = 4*sec(θ), multiplying by cos(θ) and using x = r*cos(θ) gives x = 4.
- 🔢 For r = 3*cos(θ) + 5*sin(θ), multiplying by r and using x = r*cos(θ) and y = r*sin(θ) results in x^2 + y^2 = 3x + 5y.
- 🔄 Multiplying r = 5/(2*cos(θ) + 3*sin(θ)) by the denominator and distributing r leads to the linear equation 2x + 3y = 5.
- 🔄 Using the double angle formula for sine, r^2*sin(2θ) = 8 can be converted to y = 4/x.
- 🔢 For r = 8/cos(θ), multiplying by cos(θ) and using x = r*cos(θ) gives x = 8.
- 🔄 Multiplying r = 5*cos(θ)/sin^2(θ) by sin(θ) and using cot(θ) = x/y results in y^2 = 5x.
- 🔄 For r = sin(θ)*cos^2(θ), after expanding and using x^2 + y^2 for r^2 and y for r*sin(θ), the final rectangular form is x^2 + y^2 = x√y.
Q & A
What is the main topic of the video?
-The video is about converting polar equations into rectangular equations using specific mathematical formulas.
What are the key formulas needed to convert polar equations to rectangular equations?
-The key formulas are x squared plus y squared equals r squared, x equals r cosine theta, y equals r sine theta, and tangent theta equals y divided by x.
How do you distinguish between a polar equation and a rectangular equation?
-A polar equation includes variables r or theta, while a rectangular equation consists of x and y variables.
Can you provide an example of a polar equation?
-An example of a polar equation is r equals five sine theta.
What is an example of a rectangular equation?
-An example of a rectangular equation is x squared plus y squared equals four.
How do you convert the polar equation r equals seven into a rectangular equation?
-You square both sides to get r squared equals 49, and then use the formula x squared plus y squared equals r squared, resulting in x squared plus y squared equals 49.
What happens when you have a polar equation with theta equals pi over four?
-You take the tangent of both sides, resulting in y equals x, after multiplying both sides by x.
What is the rectangular equation if theta equals zero degrees?
-In this case, y equals zero, because the tangent of zero degrees is zero, and y over x equals zero implies y equals zero.
How do you handle a polar equation where theta equals pi over two?
-Since the tangent of pi over two is undefined, you conclude that x equals zero, as this is when a function is undefined (division by zero).
If you have a polar equation r sine theta equals five, how do you convert it to rectangular form?
-You replace r sine theta with y, resulting in y equals five.
What is the rectangular form of the equation r equals 3 cosecant theta?
-You multiply both sides by sine theta to get rid of the cosecant, resulting in y equals three, using the relationship y equals r sine theta.
How do you convert the polar equation r equals 4 secant theta into a rectangular equation?
-You multiply both sides by cosine theta, resulting in x equals four, using the relationship x equals r cosine theta.
What is the rectangular form of the equation r equals 3 sine theta?
-You multiply both sides by r and use the relationships x squared plus y squared equals r squared and y equals r sine theta, resulting in x squared plus y squared equals 3y.
How do you handle the polar equation r equals 5 divided by 2 cosine theta plus 3 sine theta?
-You multiply both sides by the denominator (2 cosine theta plus 3 sine theta), distribute r, and use the relationships x equals r cosine theta and y equals r sine theta, resulting in the linear equation 2x plus 3y equals 5.
What is the rectangular form of the equation r squared sine two theta equals eight?
-You use the double angle formula for sine, divide by two, and separate r sine theta and r cosine theta, resulting in y times x equals four, and then y equals four divided by x.
How do you convert the polar equation r equals 8 divided by cosine theta into a rectangular equation?
-You multiply both sides by cosine theta, resulting in x equals eight.
What is the rectangular form of the equation r equals five cosine theta divided by sine squared theta?
-You multiply both sides by sine theta, use the relationship between tangent theta and cotangent theta, and multiply by y, resulting in y squared equals 5x.
How do you convert the polar equation r equals sine theta cosine squared theta into a rectangular equation?
-You multiply both sides by r cubed, use the relationships x equals r cosine theta and y equals r sine theta, and take the square root of both sides, resulting in x squared plus y squared equals x root y.
Outlines
🔄 Converting Polar Equations to Rectangular Equations
In this video, we discuss how to convert a polar equation into a rectangular equation. Key formulas to know include: x^2 + y^2 = r^2, x = r cos(θ), y = r sin(θ), and tan(θ) = y/x. Polar equations involve variables r and θ, while rectangular equations use x and y. Examples provided include converting r = 7 into x^2 + y^2 = 49 and θ = π/4 into y = x.
🧩 More Examples of Converting Equations
Further examples of converting polar to rectangular equations are given. These include converting r = 5 to x^2 + y^2 = 25, θ = 0 to y = 0, and θ = π/2 to x = 0. Other examples show converting r sin(θ) = 5 and r cos(θ) = 4 into y = 5 and x = 4, respectively.
📐 Complex Conversions
This section explores more complex conversions, such as r = 3 cosec(θ) to y = 3, and r = 4 sec(θ) to x = 4. The process involves multiplying both sides by sine or cosine functions and substituting the resulting expressions with x and y.
🔄 Rational Functions and Complex Equations
Converting r = 5/(2 cos(θ) + 3 sin(θ)) into 2x + 3y = 5, and r^2 sin(2θ) = 8 into y^2 = 4/x involves using trigonometric identities and manipulation. The process includes multiplying both sides by appropriate terms and rearranging the equation to isolate x and y.
📊 Final Complex Examples
Final examples include r = 8/cos(θ) converting to x = 8, and r = 5 cos(θ)/sin^2(θ) converting to y^2 = 5x. These require multiplying both sides by trigonometric terms and using identities like cot(θ) = x/y to simplify.
Mindmap
Keywords
💡Polar Equation
💡Rectangular Equation
💡Conversion
💡Right Triangle
💡r squared
💡Tangent Theta
💡Undefined
💡Cosecant
💡Secant
💡Double Angle Formula
💡Rational Function
💡Cotangent
Highlights
Introduction to converting polar equations to rectangular equations using fundamental formulas.
Explanation of the relationship between x, y, r, and theta in a right triangle context.
Formulas x^2 + y^2 = r^2, x = r * cos(theta), y = r * sin(theta), and tan(theta) = y/x are essential for conversion.
Distinguishing between polar equations with r or theta and rectangular equations with x and y variables.
Example of converting the polar equation r = 5 * sin(theta) into the rectangular form x^2 + y^2 = 49.
Method to convert r = constant into rectangular form by squaring both sides.
Approach for converting equations involving theta by using the tangent function.
Solution for theta = pi/4 resulting in y = x using the tangent function.
Handling theta = 0 degrees resulting in y = 0, as the tangent of zero is zero.
Dealing with undefined cases like theta = pi/2 by recognizing division by zero leads to x = 0.
Conversion of r * sin(theta) = 5 and r * cos(theta) = 4 directly to y = 5 and x = 4.
Using the relationship between cosecant and sine to convert r = 3 * csc(theta) to y = 3.
Conversion of r = 4 * sec(theta) by multiplying both sides by cos(theta) resulting in x = 4.
Method for converting r = 3 * sin(theta) by multiplying both sides by r and using x^2 + y^2 = r^2.
Conversion of r = 4 * cos(theta) to x^2 + y^2 = 4x by multiplying by r and using x = r * cos(theta).
Approach for converting r = 3 * cos(theta) + 5 * sin(theta) into x^2 + y^2 = 3x + 5y.
Conversion of r = 5 / (2 * cos(theta) + 3 * sin(theta)) using the denominator to simplify to 2x + 3y = 5.
Using the double angle formula to convert r^2 * sin(2 * theta) = 8 into y = 4 / x.
Conversion of r = 8 / cos(theta) to x = 8 by multiplying both sides by cos(theta).
Method for converting r = 5 * cos(theta) / sin^2(theta) to y^2 = 5x using trigonometric identities.
Conversion of r = sin(theta) * cos^2(theta) to x^2 + y^2 = x * sqrt(y) by manipulating trigonometric expressions.
Transcripts
Browse More Related Video
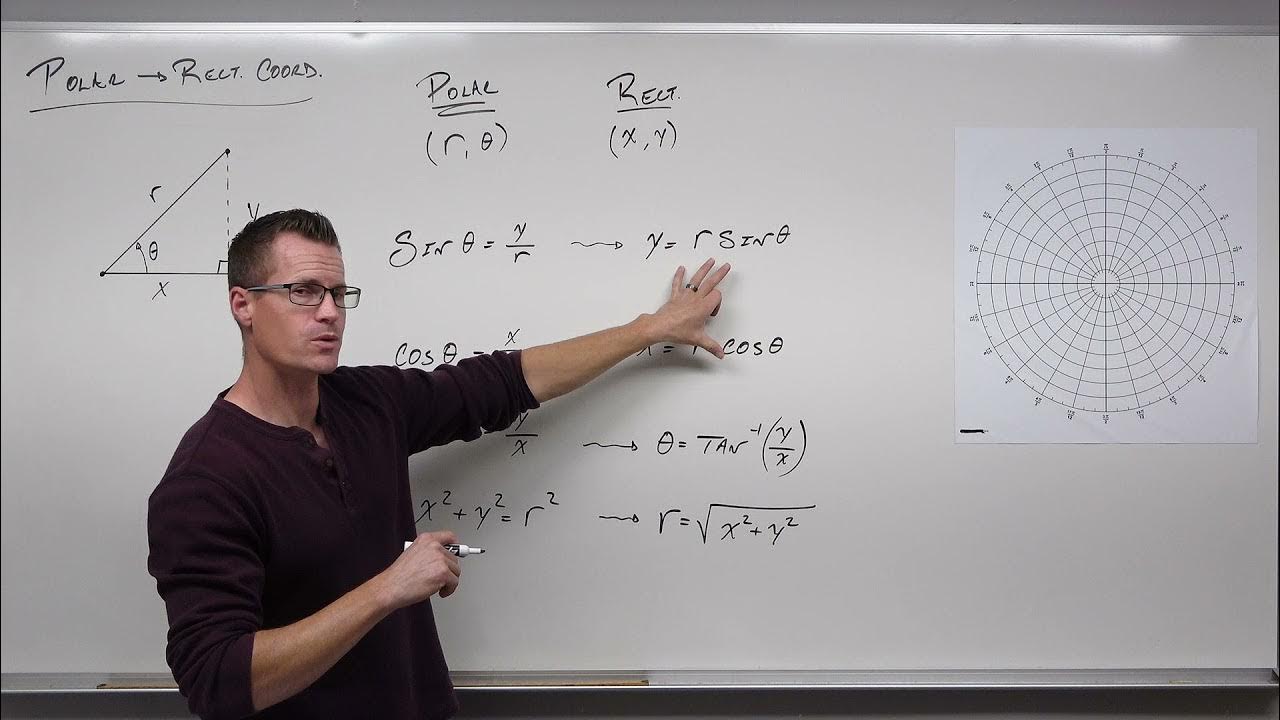
How to Convert From Polar Coordinates to Rectangular Coordinates (Precalculus - Trigonometry 37)

Rectangular Equation to Polar Equations, Precalculus, Examples and Practice Problems

How to Convert From Rectangular Equations to Polar Equations (Precalculus - Trigonometry 39)

Polar coordinates 3 | Parametric equations and polar coordinates | Precalculus | Khan Academy

How to Convert From Polar Equations to Rectangular Equations (Precalculus - Trigonometry 40)

Polar coordinates 2 | Parametric equations and polar coordinates | Precalculus | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: