How to Convert From Polar Coordinates to Rectangular Coordinates (Precalculus - Trigonometry 37)
TLDRThe video script offers a comprehensive guide on converting polar coordinates (r, θ) to rectangular coordinates (x, y) and vice versa. It emphasizes the ease of converting from polar to rectangular coordinates by leveraging the principles of right triangle trigonometry. The process involves identifying the radius (r) and angle (θ) from the polar coordinate, and then using trigonometric functions—specifically sine and cosine—to find the x and y values. The script illustrates that sine of the angle (θ) equals y/r, and cosine of the angle equals x/r, leading to the formulas y = r * sin(θ) and x = r * cos(θ). It also touches on the concept of tangent for converting rectangular back to polar coordinates and the importance of considering the quadrants to ensure accuracy. The video provides multiple examples to demonstrate the conversion process, reinforcing the understanding of mathematical concepts with practical applications.
Takeaways
- 📐 **Polar to Rectangular Conversion**: Converting polar coordinates (r, θ) to rectangular coordinates (x, y) is done using trigonometric functions: x = r * cos(θ) and y = r * sin(θ).
- 🔄 **Understanding Polar Coordinates**: Polar coordinates are represented as a distance (r) from a reference point (pole) and an angle (θ) measured from a reference direction (polar axis).
- 🧮 **Trigonometry Application**: Knowledge of sine, cosine, and tangent is essential for converting between coordinate systems, as they relate to the ratios of sides in a right triangle created by the polar coordinate point.
- 📈 **Graphing Polar Coordinates**: When graphing polar coordinates, it's important to identify the correct quadrant to ensure accurate conversion to rectangular coordinates.
- 🤔 **Quadrant Considerations**: The quadrant of the polar coordinate point affects the conversion process, especially when converting from rectangular to polar coordinates.
- ➗ **Tangent Function Role**: The tangent function (tan(θ) = y/x) is used to find the angle when converting from rectangular to polar coordinates but is limited to certain quadrants.
- 🔢 **Pythagorean Theorem**: The Pythagorean theorem is used to find the radius (r) in polar coordinates, calculated as r = √(x² + y²).
- 🔁 **Even and Odd Functions**: Cosine is an even function, and sine is an odd function, which can simplify calculations when identifying the correct quadrant for a given angle.
- 🔍 **Quadrant Verification**: Verifying the quadrant of a polar coordinate point before and after conversion helps ensure the accuracy of the conversion process.
- 🛠️ **Calculator Usage**: For angles not directly on the unit circle, use a calculator to approximate the sine and cosine values for conversion.
- ➡️ **Coordinate System Translation**: The process of converting between polar and rectangular coordinates is a translation between two different ways of representing the same point in a plane.
Q & A
What is the main topic of the video?
-The main topic of the video is converting polar coordinates to rectangular coordinates and vice versa.
What are the two types of coordinates discussed in the video?
-The two types of coordinates discussed are polar coordinates (r, θ) and rectangular coordinates (x, y).
How does one convert polar coordinates to rectangular coordinates?
-To convert polar coordinates to rectangular coordinates, you use the trigonometric functions: x = r * cos(θ) and y = r * sin(θ).
What is the significance of understanding the quadrant when converting between coordinate systems?
-Understanding the quadrant is important to ensure that the conversion from polar to rectangular or vice versa is accurate and to verify that the resulting coordinates match the expected location.
What trigonometric function is used to convert from rectangular coordinates back to polar?
-The tangent function, specifically the inverse tangent (arctangent), is used to find the angle θ when given x and y in rectangular coordinates.
Why is it necessary to consider the sign of r when converting from polar to rectangular coordinates?
-The sign of r indicates the direction from the pole along the angle θ. A negative r value indicates a direction opposite to that of a positive r, which affects the final location of the point in the rectangular coordinate system.
How can you use the Pythagorean theorem to find the value of r in polar coordinates?
-You can use the Pythagorean theorem by squaring both x and y, then taking the square root of the sum: r = √(x² + y²).
What are the advantages of converting from polar to rectangular coordinates?
-Converting from polar to rectangular coordinates is advantageous because rectangular coordinates are more commonly used and can be easier to work with in many mathematical and physical problems.
What is the role of trigonometric identities in converting between coordinate systems?
-Trigonometric identities, such as the even and odd properties of cosine and sine functions, help simplify the conversion process and allow for quicker calculations when dealing with angles that are not directly available from a unit circle or trigonometric table.
How does the video script assist in understanding the concept of converting between polar and rectangular coordinates?
-The video script provides a step-by-step explanation of the conversion process, includes examples with different types of angles and r values, and emphasizes the importance of quadrants to ensure the accuracy of the conversion.
What is the importance of checking the quadrant after converting polar coordinates to rectangular coordinates?
-Checking the quadrant helps to verify that the conversion is correct. If the calculated rectangular coordinates do not place the point in the expected quadrant based on the original polar coordinates, it indicates a mistake in the conversion process.
Outlines
📐 Introduction to Polar to Rectangular Coordinate Conversion
This paragraph introduces the concept of converting coordinates from polar (r, θ) to rectangular (x, y) form. It explains that polar coordinates are represented by a distance from the pole (r) and an angle (θ) from the polar axis. The process involves creating a right triangle by drawing a perpendicular line from the point in the polar coordinate system to the polar axis, which then corresponds to the x and y axes in the rectangular coordinate system. The trigonometric relationships sine(θ) = y/r and cosine(θ) = x/r are used to derive the conversion formulas y = r * sin(θ) and x = r * cos(θ).
🔍 Converting Rectangular to Polar and Quadrant Considerations
The second paragraph delves into the reverse process of converting rectangular coordinates to polar. It discusses the use of the tangent function and the importance of identifying the correct quadrant, as this affects the angle's measure. The Pythagorean theorem is used to find the radius (r) in polar coordinates, with r = √(x² + y²). The paragraph also touches on the challenges of converting between coordinate systems, especially when dealing with different quadrants.
📐 Working Through Examples of Polar to Rectangular Conversion
This paragraph provides step-by-step examples of converting polar coordinates to rectangular coordinates. It emphasizes the importance of identifying the radius (r) and angle (θ) from the polar coordinates and then using trigonometric functions to find the x and y values. The process is illustrated with specific examples, including checking for the correct quadrant to ensure accurate conversion.
🤔 Dealing with Quadrants and Negative Radii in Polar Coordinates
The fourth paragraph continues the discussion on coordinate conversion with a focus on handling negative radii and their effect on determining the quadrant of a point in polar coordinates. It explains that a negative radius with an angle still allows for accurate placement in the correct quadrant when converting to rectangular coordinates. The paragraph reinforces the concept that the signs of r and θ directly correspond to the location in the rectangular coordinate system.
🔢 Approximating Coordinates for Non-Standard Angles
In this paragraph, the script addresses how to handle polar coordinates with non-standard angles that are not easily found on a unit circle. It encourages the use of a calculator for approximation and stresses the importance of identifying the correct quadrant. The paragraph demonstrates the process with an example of converting a polar coordinate with a non-standard angle to its rectangular equivalent, ensuring the quadrant matches for accuracy.
🔁 Reflecting on Conversions and Anticipating Future Topics
The final paragraph reflects on the conversion process from polar to rectangular coordinates and emphasizes the utility of checking quadrants to catch errors. It previews the next topic, which will involve converting from rectangular to polar coordinates and the additional challenges this presents, such as dealing with tangent's limitation to quadrants one and four.
Mindmap
Keywords
💡Polar Coordinates
💡Rectangular Coordinates
💡Trigonometry
💡Sine Function
💡Cosine Function
💡Tangent Function
💡Quadrants
💡Pythagorean Theorem
💡Unit Circle
💡Conversion Formulas
💡Angle Measurement
Highlights
The process of converting from polar to rectangular coordinates is explained, which is easier than the reverse.
Polar coordinates are represented as r, θ, indicating distance from the pole and angle with the polar axis.
Rectangular coordinates are x, y, which are more commonly used and familiar.
Conversion from polar to rectangular is achieved by creating a right triangle and applying trigonometric functions.
The relationships y = r * sin(θ) and x = r * cos(θ) are used to convert polar coordinates to rectangular.
Trigonometric functions sine, cosine, and tangent are fundamental to the conversion process.
The tangent function is used to convert from rectangular to polar, with the formula tan(θ) = y/x.
The Pythagorean theorem is applied to find the radius r in rectangular to polar conversion, with r = √(x² + y²).
Quadrants are important when converting from rectangular to polar to ensure the correct angle is used.
The video provides a step-by-step guide to converting specific polar coordinates to rectangular coordinates.
Checking the quadrant of a point is a good practice to ensure the accuracy of the conversion.
The video demonstrates converting multiple examples of polar coordinates into rectangular coordinates.
Negative r values in polar coordinates are handled by understanding the reflection across the pole.
The importance of keeping the correct order (x, y for rectangular and r, θ for polar) is emphasized.
The video concludes with a summary of the methods for converting between polar and rectangular coordinates.
Practical examples are used to illustrate the conversion process and to check for understanding.
The video mentions that the next video will cover converting from rectangular to polar coordinates.
Transcripts
Browse More Related Video

Polar coordinates 2 | Parametric equations and polar coordinates | Precalculus | Khan Academy
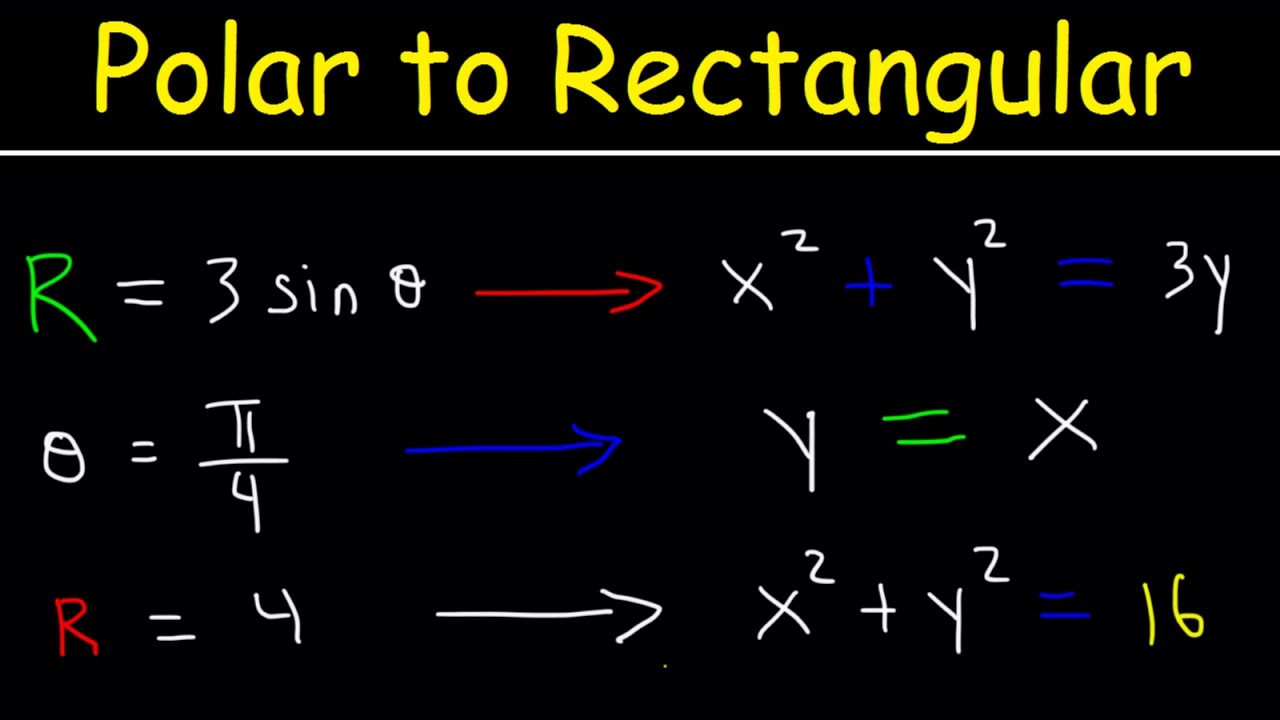
Polar Equations to Rectangular Equations, Precalculus, Examples and Practice Problems

Polar coordinates 3 | Parametric equations and polar coordinates | Precalculus | Khan Academy

How to Convert From Rectangular Equations to Polar Equations (Precalculus - Trigonometry 39)

Polar coordinates 1 | Parametric equations and polar coordinates | Precalculus | Khan Academy
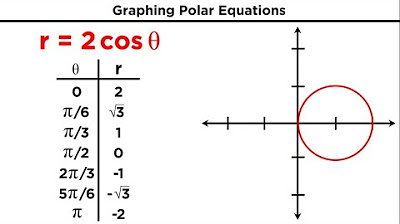
Polar Coordinates and Graphing Polar Equations
5.0 / 5 (0 votes)
Thanks for rating: