Notes on Polar, Day 3

Chad Gilliland
26 Mar 201408:59
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video script explores the concept of finding areas within and between polar curves. It demonstrates the process of graphing and calculating the area inside a circle with a diameter of three, represented by R = 3 sin(Θ), and outside a convex lison, R = 2 - sin(Θ), by identifying their points of intersection at Θ = π/6 and 5π/6. The script also covers finding the common interior area between a circle and a cardioid, R = 3 cos(Θ) and R = 1 + cos(Θ), using symmetry and integrals to set up the expressions for the area calculations without evaluating them. The importance of locating intersection points for calculating areas of common interiors or areas inside one curve and outside another is emphasized.

Takeaways
  • 📚 The lesson is about finding the area of polar curves, specifically focusing on areas inside and outside intersecting curves.
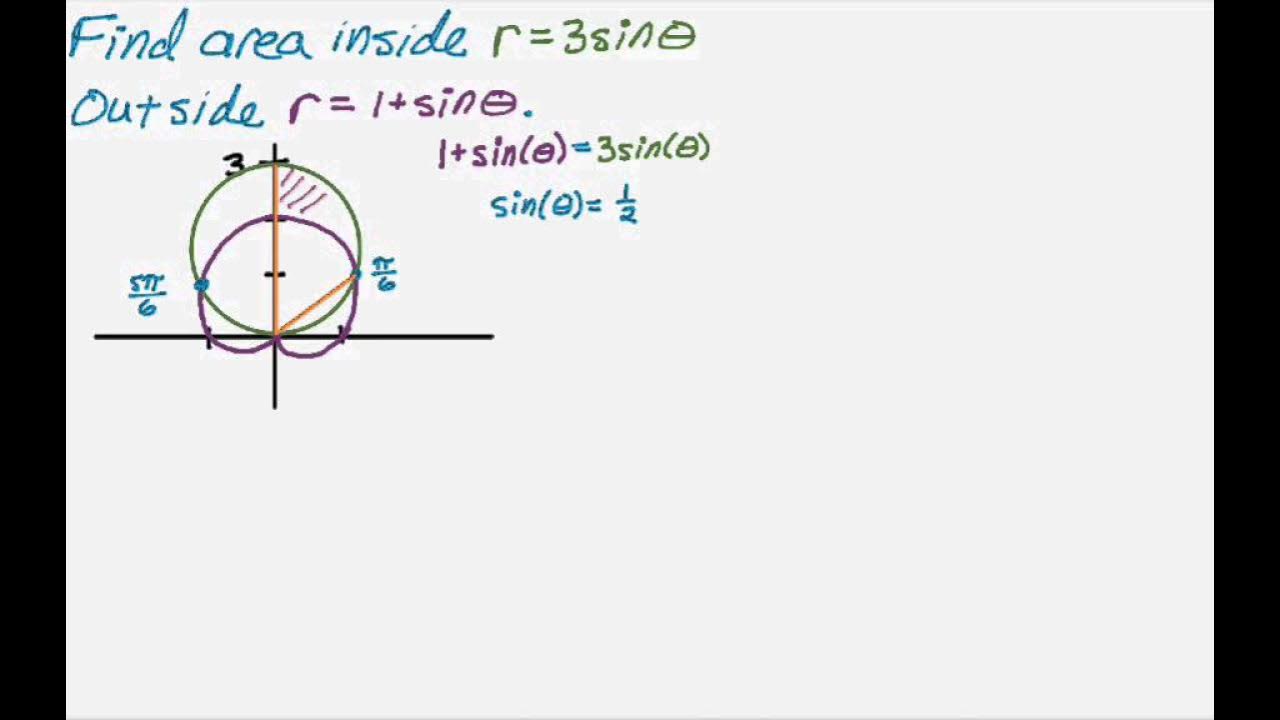
  • 📈 The first example involves the polar curve R = 3 sin(Theta), which is a circle with a diameter of three, vertical and centered at the pole.
  • 📉 The second curve is R = 2 - sin(Theta), which is a dimpled or convex lissenkot, and does not have an inner loop because 'a' is larger than 'b' in magnitude.
  • 🔍 To find the area of interest, the instructor emphasizes the importance of identifying the points of intersection between the two curves.
  • 📐 The points of intersection for the given curves are found by setting 3 sin(Theta) equal to 2 - sin(Theta), leading to Theta values of pi/6 and 5pi/6.
  • 📝 The area calculation involves using symmetry and integrals to find the area inside the circle but outside the lissenkot between the identified angles.
  • 📉 The second part of the lesson discusses finding the common interior area between the curves R = 3 cos(Theta), a circle, and R = 1 + cos(Theta), a cardioid.
  • 🔍 For the common interior area, the points of intersection are also crucial and are found by setting 3 cos(Theta) equal to 1 + cos(Theta), resulting in Theta values of pi/3 and 5pi/3.
  • 📝 The area calculation for the common interior involves using the cardioid equation until the point of intersection and then switching to the circle's equation for the remaining area.
  • 📈 The instructor uses symmetry to simplify the calculations by considering only one half of the图形 and then doubling the result.
  • 😄 The script includes a humorous note about the instructor's own graphing skills, suggesting a light-hearted approach to the lesson.
Q & A

  • What is the first step in finding the area inside one polar curve and outside another?

    -The first step is to graph the polar curves and identify the regions of interest. In the example, the curves are 3 sin(θ) and 2 - sin(θ).

  • How do you determine the points of intersection for the polar curves?

    -To find the points of intersection, set the equations of the polar curves equal to each other and solve for θ. For example, set 3 sin(θ) = 2 - sin(θ) and solve for θ.

  • What values of θ are found for the intersection points in the example with 3 sin(θ) and 2 - sin(θ)?

    -The values of θ for the intersection points are π/6 and 5π/6.

  • How is symmetry used to simplify the area calculation?

    -Symmetry is used by calculating the area of one symmetric region and then doubling it to get the total area. For example, calculate the area from π/6 to π/2 and then double it.

  • What integral expression represents the area inside the circle but outside the limacon?

    -The area is given by the integral expression: 2 * (1/2 ∫[π/6 to π/2] 9 sin²(θ) dθ - 1/2 ∫[π/6 to π/2] (2 - sin(θ))² dθ).

  • How do you find the area of the common interior of two polar curves?

    -To find the common interior area, set up integrals for each section where one curve is inside the other, ensuring to find the points of intersection and use the correct limits of integration.

  • What are the points of intersection for the curves 3 cos(θ) and 1 + cos(θ)?

    -The points of intersection for the curves 3 cos(θ) and 1 + cos(θ) are at θ = π/3 and θ = 5π/3.

  • How do you write the integral expression for the common interior area of 3 cos(θ) and 1 + cos(θ)?

    -The integral expression for the common interior area is: 2 * (1/2 ∫[0 to π/3] (1 + cos(θ))² dθ + 1/2 ∫[π/3 to π/2] 9 cos²(θ) dθ).

  • Why is it important to find the points of intersection when dealing with polar curves?

    -Finding the points of intersection is crucial because they determine the limits of integration for calculating the areas inside and outside the curves, or the common interior.

  • What does the script mean by 'taking advantage of symmetry' in the context of calculating areas?

    -Taking advantage of symmetry means calculating the area of one symmetrical section and then multiplying by the number of symmetrical sections, thereby simplifying the calculation process.

Outlines
00:00
📚 Finding Areas of Polar Curves

This paragraph introduces the concept of finding areas of polar curves, specifically focusing on the area inside one curve but outside another. The example given involves the curves R = 3 sin(Θ) and R = 2 - sin(Θ). The first curve is identified as a circle with a diameter of three, while the second is a cardioid. The speaker discusses the importance of graphing these curves to understand their shapes and intersections. The goal is to find the area inside the circle but outside the cardioid, which requires identifying the points of intersection. The intersection points are found by setting the two equations equal to each other, resulting in Θ values of π/6 and 5π/6. The strategy involves calculating the area from π/6 to π/2 using the circle's equation, then subtracting the area inside the cardioid, which is done by integrating the respective equations over the specified range.

05:03
🎨 Common Interiors and Intersection Points

In this paragraph, the focus shifts to finding the common interior area between two polar curves: R = 3 cos(Θ), which is a circle, and R = 1 + cos(Θ), a cardioid. The speaker emphasizes the importance of identifying the points of intersection to determine the boundaries of the area of interest. The intersection points are calculated by setting the two equations equal to each other, yielding Θ values of π/3 and 5π/3. The strategy involves calculating the area using the cardioid's equation from 0 to π/3, and then using the circle's equation from π/3 to π/2. The speaker also highlights the use of symmetry to simplify the calculations, effectively doubling the calculated area to account for the entire region of interest. The emphasis is on the methodical approach to finding these areas, including the setup of integral expressions without necessarily evaluating them.

Mindmap
Keywords
💡Polar Curves
Polar curves are mathematical representations of points in the polar coordinate system, where each point is defined by its distance from the origin (radius) and the angle it makes with the positive x-axis (theta). In the video, polar curves are used to describe the shapes of geometric figures such as circles and cardioids, and to calculate the area enclosed by these curves.
💡Area
The term 'area' refers to the measure of the two-dimensional space enclosed within a shape or a set of boundaries. In the context of the video, the area is calculated for regions bounded by polar curves, which is essential for understanding the geometric properties of these shapes.
💡Intersection Points
Intersection points are the points where two or more curves meet. In the video, finding the intersection points of polar curves is crucial for determining the boundaries of the area to be calculated. For instance, the script discusses finding when '3 sin Theta equals 2 - sin Theta' to identify the points where the circle and the cardioid intersect.
💡Symmetry
Symmetry in the context of the video refers to the property of a shape that allows it to be divided into parts that are mirror images of each other. The script uses symmetry to simplify the calculation of areas by focusing on a part of the shape and then doubling the result to account for the entire area.
💡Integral
An integral is a mathematical concept used to calculate the area under a curve or between curves. In the script, integrals are used to find the area enclosed by polar curves by integrating expressions derived from the polar equations over a specific interval.
💡Circle
A circle is a geometric shape defined by all points that are equidistant from a central point, known as the center. In the video, the circle is represented by the polar equation 'R = 3 sin Theta', which describes a circle with a diameter of three units.
💡Cardioid
A cardioid is a type of curve shaped like a heart, often found in polar coordinates. The script mentions '2 - sin Theta' as an example of a cardioid, which is a specific case where the polar equation results in a heart-shaped figure.
💡Lemniscate
A lemniscate is another type of polar curve, mentioned in the script as '2 - sin Theta', which is a figure-eight shape. The term is used to describe the shape that is not a cardioid and has a different area calculation method.
💡Graphing
Graphing is the process of visually representing data or equations on a coordinate system. In the video, graphing is used to illustrate the shapes of polar curves and to identify the areas of interest for area calculations.
💡Pi
Pi (π) is a mathematical constant representing the ratio of a circle's circumference to its diameter, approximately equal to 3.14159. In the script, pi is used in the context of angles in radians for polar coordinates, such as 'pi/6' and '5pi/6', which are used to find the angles of intersection.
💡Cosine
Cosine is a trigonometric function that relates the angle of a right triangle to the ratio of the lengths of its sides. In the video, cosine is used in the polar equations '3 cosine Theta' and '1 + cosine Theta' to describe the shapes of a circle and a cardioid, respectively.
Highlights

Introduction to finding the area of polar curves, specifically areas inside and outside intersecting curves.

Explanation of the graph of R = 3 sin Theta, identifying it as a circle with a diameter of three.

Graphical representation of the circle and its properties based on the polar equation.

Description of the graph of R = 2 - sin Theta, identifying it as a convex lison without an inner loop.

Graphical illustration of the lison and its properties based on the polar equation.

Objective to find the area inside the circle but outside the lison.

Methodology to find the area by integrating from the point of intersection.

Use of symmetry to simplify the calculation by doubling the area found from one segment.

Setting up the integral expression for the area calculation without evaluating it.

Introduction to finding the common interior area between two polar curves.

Graphical representation of the circle R = 3 cos Theta and its properties.

Description of the graph of R = 1 + cos Theta, identifying it as a cardioid.

Objective to find the common interior area between the circle and the cardioid.

Finding the points of intersection between the circle and the cardioid.

Strategy to calculate the area using the cardioid equation until the point of intersection and then switching to the circle's equation.

Use of symmetry to simplify the calculation by doubling the area found from one segment for the common interior.

Emphasis on the importance of finding points of intersection in polar curve area calculations.

Transcripts

Browse More Related Video

Calculus Polar Area Region Between Curves Example

How To Graph Polar Equations

Graph of r = 1 + cos(theta/2) | MIT 18.01SC Single Variable Calculus, Fall 2010

Calculus Polar Area Rose Curve Example

Arc Length of a Circle Formula - Sector Area, Examples, Radians, In Terms of Pi, Trigonometry

AP Precalculus Practice Exam Question 15

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Polar CurvesArea CalculationMathematicsEducational ContentGraphingCirclesCardioidsIntegral CalculusSymmetryIntersection Points