Vectors Full Topic -Physics
TLDRThis comprehensive tutorial delves into the fundamental concepts of vectors, a critical topic in physics and mathematics. The instructor begins by distinguishing between vector and scalar quantities, emphasizing that vectors possess both magnitude and direction, exemplified through physical quantities like force and velocity. The video illustrates how to calculate the resultant vector from parallel vectors by adding their magnitudes directly or using trigonometric functions for vectors at angles. It also addresses the addition of vectors not aligned in a single plane, introducing the components of vectors in different quadrants and how to resolve them into X and Y components. The tutorial progresses to sketching vectors, resolving them into components, and finding the magnitude and direction of the resultant vector. The instructor provides step-by-step instructions for these processes, including the use of Pythagoras' theorem and the application of trigonometric ratios. The script concludes with practice questions that reinforce the concepts taught, guiding learners through the application of these principles to solve real-world problems involving vector addition, direction, and magnitude.
Takeaways
- 📐 **Vectors and Scalars**: A vector is a physical quantity with both magnitude and direction, while a scalar has only magnitude.
- 🚗 **Direction in Vectors**: The direction of a vector is crucial, indicating the orientation, such as south or east, and is combined with its magnitude.
- 🔵 **Vector Examples**: Examples of vector quantities include force, momentum, acceleration, velocity, and displacement.
- 🔵 **Scalar Examples**: Examples of scalar quantities include distance, mass, time, and speed.
- ➕ **Vector Addition**: Vectors can be added together, resulting in a new vector known as the resultant vector, which combines both magnitude and direction.
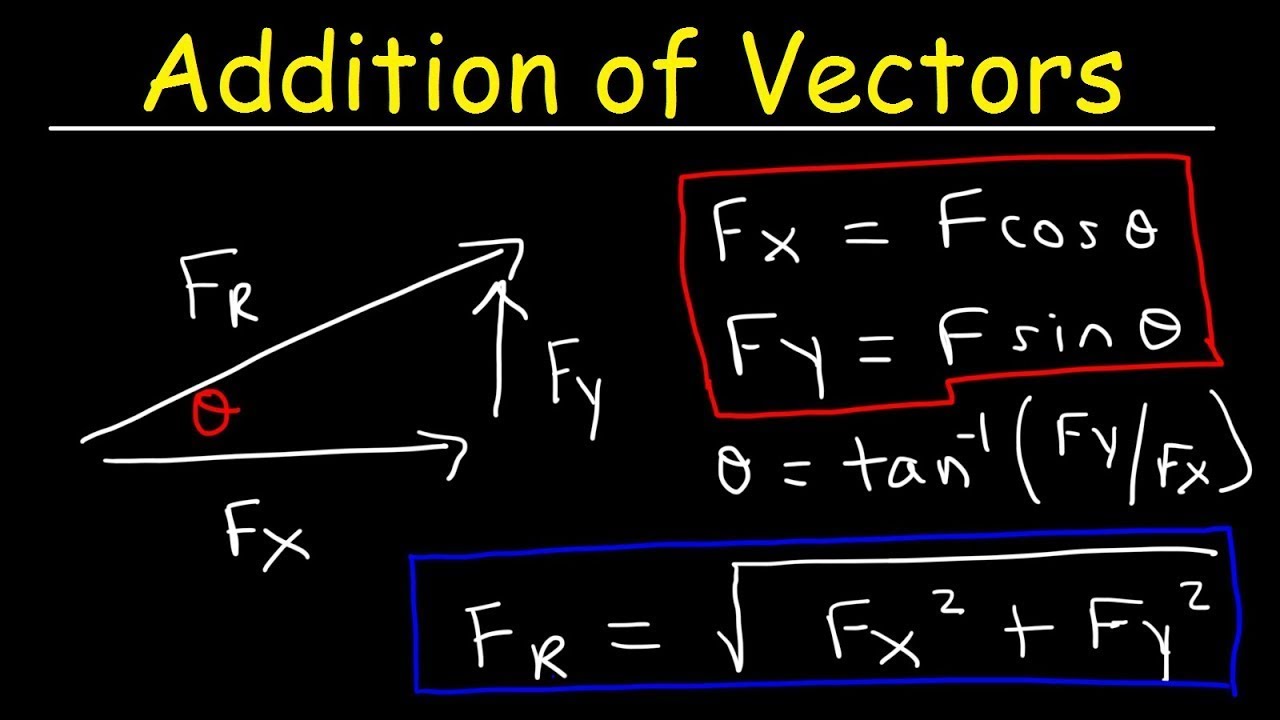
- ➗ **Perpendicular Vectors**: When vectors are perpendicular, their resultant is found using Pythagoras' Theorem, \( \sqrt{a^2 + b^2} \).
- 🔄 **Resolving Vectors**: Vectors can be broken down into components along the X and Y axes using trigonometric functions like sine and cosine.
- 🔢 **Negative Vectors**: A vector can have a negative value, which indicates the opposite direction along the same magnitude.
- 📈 **Resultant Vector**: The resultant vector is the sum of all vectors being added and is found by adding the X and Y components separately.
- 🔀 **Non-Perpendicular, Non-Parallel Vectors**: When vectors are neither perpendicular nor parallel, their components are found using the angle between them and then combined to find the resultant.
- 📝 **Free Body Diagrams (FBD) vs. Sketching**: FBDs are diagrams that represent forces and vectors as understood by the person creating them, while sketching provides an exact visual representation of the vectors as given.
Q & A
What is the fundamental difference between a vector and a scalar quantity?
-A vector quantity is a physical quantity that has both magnitude and direction, whereas a scalar quantity has only magnitude without any direction.
What are some examples of vector quantities?
-Examples of vector quantities include force, momentum, acceleration, velocity, and displacement.
How do you find the resultant of two parallel vectors?
-To find the resultant of two parallel vectors, you simply add their magnitudes while considering their directions. If they are in the same direction, you add the magnitudes directly. If they are in opposite directions, you subtract the smaller magnitude from the larger one.
How is the magnitude of a resultant vector calculated when the vectors are perpendicular to each other?
-The magnitude of the resultant vector of two perpendicular vectors is calculated using the Pythagorean theorem: it is the square root of the sum of the squares of the magnitudes of the individual vectors (i.e., √(a² + b²)).
What is the significance of the direction in vector addition?
-The direction is significant in vector addition because it determines the final direction of the resultant vector. When adding vectors, you must consider both the magnitudes and the directions to accurately find the resultant vector.
How do you resolve a vector into its horizontal (X) and vertical (Y) components?
-To resolve a vector into its horizontal (X) and vertical (Y) components, you use the angle of the vector with respect to the horizontal axis. The horizontal component is found by multiplying the vector's magnitude by the cosine of its angle (a_x = a * cos(θ)), and the vertical component is found by multiplying the vector's magnitude by the sine of its angle (a_y = a * sin(θ)).
What is the formula to find the angle of a vector when only its components are known?
-The formula to find the angle (Θ) of a vector when only its X and Y components are known is Θ = tan^(-1)(Y_component / X_component).
How do you determine the quadrant in which the angle of a vector lies?
-The quadrant of the angle of a vector is determined by the signs of its X and Y components. A vector with a positive X component and a positive Y component lies in the first quadrant. If the X component is negative and the Y component is positive, it lies in the second quadrant. For negative X and Y components, it is in the third quadrant, and if the X component is positive and the Y component is negative, it lies in the fourth quadrant.
What is the difference between sketching vectors and drawing a free body diagram?
-Sketching vectors involves drawing vectors to scale with accurate representations of their magnitudes and directions, often for visual or instructional purposes. A free body diagram, on the other hand, is a representation used to analyze the forces acting on a body, where the scale and precise lengths are not necessary for understanding the forces involved.
What is the resultant vector when a ship initially heads 120 kilometers north but is then blown 100 kilometers east by a storm?
-To find the resultant vector, you can use the Pythagorean theorem, considering the northward journey and the eastward drift as perpendicular components. The magnitude of the resultant vector is √(120² + 100²) = √(14400 + 10000) = √24400 ≈ 156.2 kilometers. The direction is found using the arctan function, which gives an angle of 50.2 degrees from the north, towards the east.
How do you find the magnitude and direction of a vector when given its components in a rotated coordinate system?
-To find the magnitude, you calculate the square root of the sum of the squares of the components (i.e., √(x_component² + y_component²)). To find the direction, you use the arctan function to get the angle from the horizontal axis, taking into account the quadrant in which the vector lies to adjust the angle if necessary.
Outlines
📚 Introduction to Vectors and Scalars
This paragraph introduces the concept of vectors as physical quantities with both magnitude and direction. It distinguishes between vector and scalar quantities, with examples provided for each. The importance of direction in defining a vector is emphasized, and basic vector operations such as addition are introduced.
📝 Adding Parallel Vectors
The second paragraph focuses on adding parallel vectors by simply summing their magnitudes. It explains that the direction is crucial in vector addition and introduces the concept of the resultant vector, which is the sum of all vectors involved.
🔢 Vector Addition with Directional Considerations
This part delves into vector addition when vectors are not parallel, highlighting the need to consider direction. It explains how to find the resultant of vectors with different directions, including those moving in opposite directions, and how to handle negative values in vector calculations.
🔍 Resolving Perpendicular Vectors
The fourth paragraph discusses the addition of perpendicular vectors using the Pythagorean theorem. It provides a step-by-step method to calculate the resultant vector's magnitude and direction when the vectors are at a 90-degree angle to each other.
🦞 Vector Components and Direction
This segment explains how to find the components of a vector and its direction. It covers the use of trigonometric functions to resolve a vector into its X and Y components and how to calculate the direction angle of a vector.
🧭 Finding Vector Components and Resultant Direction
The paragraph explains how to find the X and Y components of a vector given its magnitude and direction angle. It also details the process of finding the resultant vector's direction using the arctan function and how to adjust for different quadrants.
📐 Sketching Vectors and Resultants
This part covers the process of sketching vectors on an X-Y plane and finding the resultant vector by connecting the endpoints of individual vectors. It emphasizes the importance of understanding vector directions and their impact on the resultant's magnitude and direction.
📏 Vector Resolution and Resultant Calculation
The seventh paragraph demonstrates how to resolve vectors into their components and calculate the resultant vector. It provides a method to find the magnitude and direction of the resultant vector by summing the components and applying trigonometric principles.
📐 Sketching Vectors in a Plane
This segment focuses on the process of sketching vectors on an X-Y plane given their magnitudes and directions. It explains how to accurately represent vectors and their directions to find the resultant vector graphically.
🔢 Vector Components in Different Quadrants
The ninth paragraph discusses how to determine the angle associated with a vector based on its position in different quadrants. It explains the concept of clockwise rotation and how it affects the calculation of vector components.
📐 Sketching and Free Body Diagrams
This part distinguishes between sketching vectors and creating free body diagrams. It explains that sketching represents vectors as they are, while free body diagrams are simplified representations for the solver's understanding.
🧮 Calculating Vector Components and Resultants
The final paragraph provides a detailed method for calculating the X and Y components of vectors given their magnitude and direction. It also explains how to find the resultant vector by summing individual vectors' components.
Mindmap
Keywords
💡Vectors
💡Scalar Quantity
💡Magnitude
💡Direction
💡Resultant Vector
💡Parallel Vectors
💡Perpendicular Vectors
💡Free Body Diagram (FBD)
💡Vector Resolution
💡Trigonometry
💡Quadrants
Highlights
Vectors are physical quantities with both magnitude and direction, contrasting with scalars which only have magnitude.
The introduction of vector and scalar quantities, including examples such as force, momentum, and distance.
The concept of vector addition, specifically for parallel vectors, resulting in the resultant vector.
Explanation of how negative values relate to vector direction, particularly in the context of velocity versus speed.
The use of Pythagoras' Theorem to find the resultant of perpendicular vectors.
The method for resolving vectors into their X and Y components using trigonometric functions.
Determination of a vector's angle of direction using the arctan function (tan inverse).
Procedure for finding the components of a vector given its magnitude and direction angle.
How to resolve a vector into its components when it lies in different quadrants, adjusting for the angle's position.
The process for sketching vectors accurately on an X-Y plane, including the use of angles and magnitudes.
Explanation of how to find the resultant vector by adding individual vectors' components and then calculating its magnitude and direction.
The difference between sketching vectors and creating a free body diagram (FBD), with an emphasis on the purpose of each.
Guidelines on how to represent vectors on a free body diagram, including the use of directional terms like 'north of east'.
Conversion of angles from degrees to radians and vice versa, emphasizing the mathematical relationships between these units of measure.
Application of vector concepts to real-world problems, such as calculating the displacement of a ship affected by a storm.
Use of vector addition to determine the straight-line distance and direction from a starting point to an ending point after multiple directional movements.
Solution to finding the components of vectors in a new coordinate system inclined to the original, using trigonometric functions.
Method for calculating the magnitude of a vector when given its components in different coordinate systems.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: