Resultant vector | Vector addition: Grade 10 Physics
TLDRThe video script delves into the concept of vectors in physics, emphasizing the importance of both magnitude and direction in determining the net or resultant vector. It explains that vectors represent physical quantities with direction and magnitude, and neglecting direction can lead to incorrect answers. The script illustrates how to calculate the net force by adding vectors, considering their directions as positive or negative based on the chosen reference. It also clarifies that only vectors of the same type can be added together, such as force vectors or displacement vectors. The process of vector addition is demonstrated through various examples, including forces acting on a box and graphical representations using tail-to-head or head-to-tail diagrams. The script concludes with an example problem involving three forces acting on an object, guiding viewers on how to find the resultant force by correctly applying vector addition and direction considerations.
Takeaways
- 📏 **Magnitude and Direction**: Vectors have both magnitude (size) and direction, which are crucial for accurate representation and calculations.
- ➡️ **Direction Importance**: Omitting direction when dealing with vectors can lead to incorrect answers.
- 🤝 **Vector Addition**: When adding vectors, their directions must be considered, especially when they are not aligned.
- ⚖️ **Net Force Calculation**: The net force is determined by adding forces acting on the same object at the same time, considering their directions.
- 🔴 **Positive and Negative Directions**: In vector addition, one direction is chosen as positive, and the opposite direction is considered negative.
- 🏷️ **Vector Representation**: Single vectors are depicted by arrows, where the length signifies magnitude, and the arrowhead indicates direction.
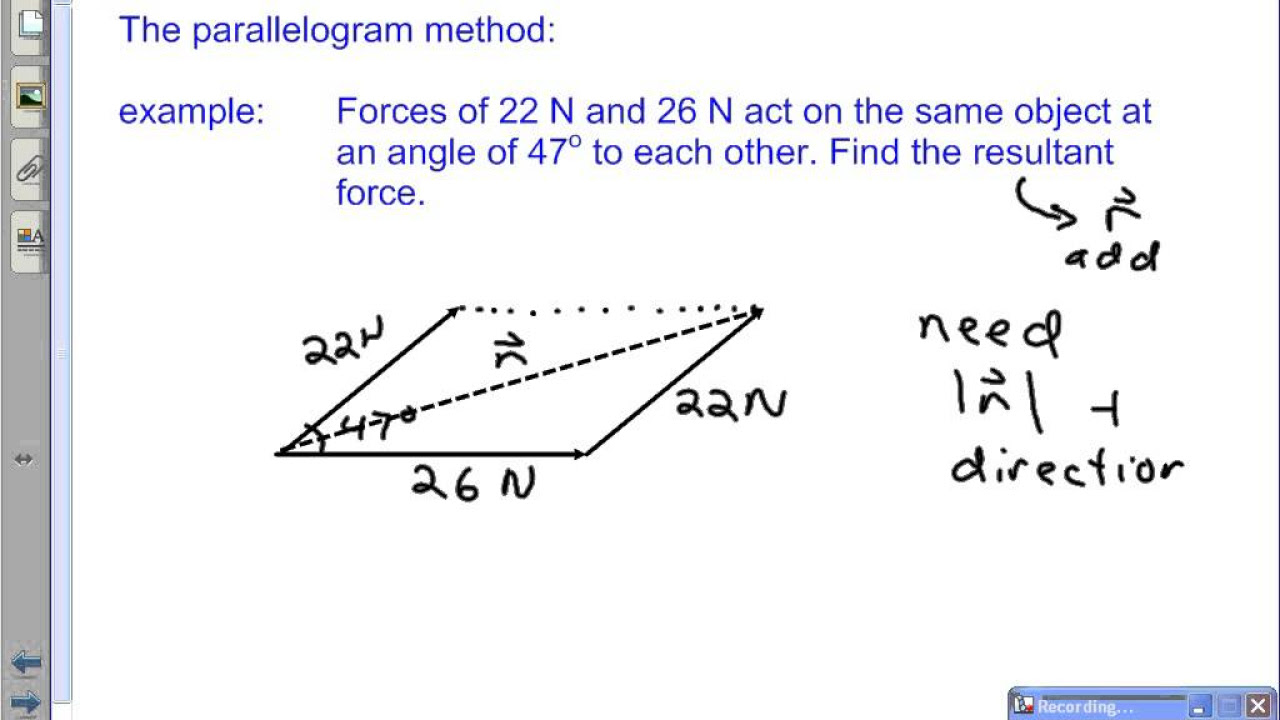
- 🔀 **Resultant Vector Definition**: A resultant vector is the sum of two or more vectors, having the same effect as all the individual vectors combined.
- ✅ **Same-Type Vectors**: Only vectors of the same type (e.g., force, acceleration, displacement) can be added together.
- 🔢 **Algebraic Vector Addition**: Vectors are added algebraically, considering their directions as positive or negative based on the chosen reference direction.
- 📉 **Interpreting Negative Results**: A negative result in vector addition indicates the direction opposite to the chosen positive direction.
- 📚 **Graphical Representation**: Tail-to-head or head-to-tail diagrams are used to visually represent the addition of vectors, aiding in understanding the resultant vector.
Q & A
What is a vector and why is direction important when dealing with vectors?
-A vector is a physical quantity that has both magnitude and direction. Direction is crucial when dealing with vectors because it determines the orientation of the vector in space. If the direction is not included as part of the answer, the result could be incorrect.
How do you represent a single vector?
-A single vector is represented by an arrow, where the length of the arrow represents the magnitude or size of the vector, and the arrowhead points in the direction the vector is pointing in.
What is a resultant vector and how is it different from individual vectors?
-A resultant vector is the vector sum of two or more vectors added together. It is a single vector that has the same effect as two or more vectors acting together. It is different from individual vectors because it represents the combined effect of multiple vectors.
When adding vectors, why is it necessary to consider their directions?
-When adding vectors, their directions need to be considered because the direction affects the outcome of the vector sum. Vectors can be in the same direction, opposite directions, or at various angles to each other, and this influences how they are mathematically added together.
What is the correct procedure to calculate the net force or resultant vector when forces are acting in opposite directions?
-To calculate the net force or resultant vector when forces are acting in opposite directions, you first choose a positive direction. Then, you represent the forces in terms of their magnitudes and the chosen direction, using positive for the chosen direction and negative for the opposite. You then add these values, considering their signs, to find the net force.
Why is it important to only add vectors of the same type together?
-It is important to only add vectors of the same type together because different types of vectors represent different physical quantities (like force, acceleration, displacement, momentum) and cannot be combined mathematically in a meaningful way.
How do you interpret a negative answer when calculating the resultant vector?
-A negative answer when calculating the resultant vector indicates that the direction of the resultant vector is opposite to the chosen positive direction. For example, if the positive direction is to the right and the answer is negative, it means the resultant vector is to the left.
What is the head-to-tail method for graphical representation of vectors?
-The head-to-tail method is a graphical technique for representing vectors where the tail of one vector is placed at the head of the next vector. This method helps visualize the addition of vectors and the resultant vector.
How do you calculate the resultant force on an object when three forces are acting on it?
-To calculate the resultant force on an object when three forces are acting on it, you first choose a positive direction. Then, you represent each force with its magnitude and the sign corresponding to its direction (positive or negative). Finally, you add these values together to find the net or resultant force.
What is the significance of the magnitude and direction in determining the resultant vector of multiple vectors?
-The magnitude and direction of each vector are significant in determining the resultant vector because they dictate the overall strength and orientation of the combined vector. The magnitude affects the length of the resultant, while the direction dictates the orientation in space.
How does the direction of a vector impact the calculation of the net force in a system?
-The direction of a vector impacts the calculation of the net force in a system because it determines whether the vectors will add up or subtract from each other. Vectors in the chosen positive direction add up, while vectors in the opposite direction are subtracted, reflecting the physics of forces acting in different orientations.
Outlines
📐 Understanding Vectors and Resultant Vectors
This paragraph introduces the concept of vectors, emphasizing their physical significance and the importance of direction in vector calculations. It explains that failing to account for direction can lead to incorrect answers. The paragraph also discusses the process of adding vectors, particularly when they are in opposite directions, and the need to consider positive and negative directions. It defines a resultant vector as the sum of two or more vectors, which can be represented as a single vector with the same effect. The representation of single vectors using arrows is mentioned, where the arrow's length indicates magnitude, and its direction indicates orientation. The paragraph concludes with an example of adding vectors that are not in the same direction, illustrating how to determine the net or resultant vector, including considerations for positive and negative directions.
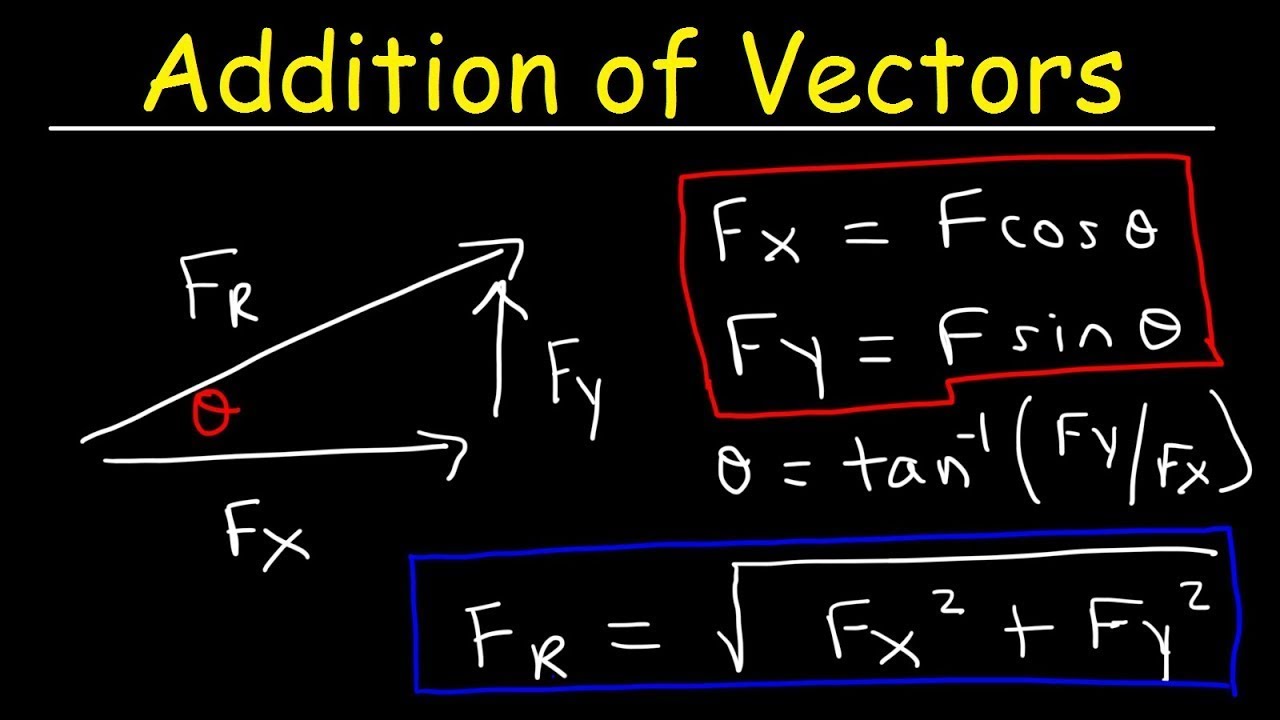
🔢 Algebraic Vector Addition and Choosing a Positive Direction
The second paragraph delves into the algebraic aspect of vector addition, focusing on choosing a positive direction to determine the resultant vector. It outlines the process of adding vectors with different directions, using positive and negative signs to indicate direction. The paragraph provides an example of adding vectors that are not aligned, explaining how to interpret the signs and perform the addition to find the net vector. It also touches on the concept of vector sum and how it applies to finding the resultant vector. The importance of indicating the chosen positive direction during an exam is highlighted. The paragraph concludes with examples of vector addition, including scenarios where vectors are in the same or opposite directions, and the need to rewrite answers with a positive interpretation, considering the chosen direction.
🧮 Calculating Resultant Vectors with Multiple Forces
The third paragraph presents a detailed approach to calculating resultant vectors, particularly when multiple forces are acting on an object. It explains the concept of vector sum and how it is used to find the resultant force when vectors are added together. The paragraph provides a step-by-step guide on how to choose a positive direction and apply it to the calculation of the net force. It includes examples where forces are acting in the same or opposite directions, demonstrating how to substitute the correct signs into the vector sum equation. The paragraph concludes with a problem-solving scenario involving three forces acting on a body, illustrating the process of determining the resultant force by adding the individual forces with their respective directions and signs.
Mindmap
Keywords
💡Vectors
💡Magnitude
💡Direction
💡Resultant Vector
💡Vector Sum
💡Positive and Negative Directions
💡Net Force
💡Algebraic Vector Addition
💡Force Vectors
💡Displacement Vectors
💡Head-to-Tail Method
Highlights
Vectors have both magnitude and direction, with direction being crucial for accurate representation.
Failure to include direction in vector calculations can lead to incorrect answers.
When adding vectors, their directions must be considered, especially when they act in opposite ways.
A single vector can represent the sum of two or more vectors, known as the resultant vector.
The length of an arrow in a vector diagram represents the vector's magnitude.
The direction of the arrowhead indicates the direction in which the vector is pointing.
Resultant vectors are calculated by adding vectors that act on the same object at the same time and in the same direction.
Only vectors of the same type can be added together, such as force vectors with other force vectors.
A graphical representation of vectors can be done using a tail-to-head or head-to-tail diagram.
When vectors point in different directions, algebraic addition with consideration of positive and negative signs is used.
The net or resultant vector is found by adding vectors, considering their directions as positive or negative.
A negative result in vector addition implies the direction opposite to the chosen positive direction.
Graphical representation helps visualize vector addition and the calculation of the resultant vector.
In physics problems, forces acting on an object can be represented as vectors and their resultant calculated.
The direction indicated by the resultant vector shows the net direction of all the forces acting on the object.
Understanding vector addition is essential for solving problems involving forces, acceleration, displacement, and momentum.
The magnitude and direction of the resultant vector provide the total effect of multiple vectors acting together.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: