Addition of Vectors By Means of Components - Physics
TLDRThis video script presents a comprehensive guide on vector addition, explaining the concepts of magnitude and direction in the context of force vectors. It illustrates how to calculate the resultant force when vectors are parallel, anti-parallel, perpendicular, and at various angles to each other. The script uses clear examples and mathematical formulas to demonstrate how to find both the magnitude and direction of the resultant force vector, employing components and trigonometric relationships for accurate calculations.
Takeaways
- 📐 Vectors have both magnitude (size) and direction, like a force vector with 100 newtons towards the east.
- 🔄 To add parallel vectors, simply sum their magnitudes to get the resultant force.
- 🔢 When adding vectors with opposite directions, represent them as positive and negative values, and calculate the net force.
- 📈 The resultant vector's magnitude is found using the Pythagorean theorem (sqrt(f1^2 + f2^2)) when vectors are perpendicular.
- 📊 To find the direction of the resultant vector, use the arctangent formula (tan^(-1)(y-component/x-component))
- 🌐 For non-parallel or non-perpendicular vectors, break them into components and use the Pythagorean theorem and arctangent to find the resultant.
- 🔄 When adding vectors at an angle, convert the angle to its cosine and sine components to find the x and y components.
- 📐 The magnitude of the resultant vector from components is calculated using the Pythagorean theorem.
- 🧭 The direction from the positive x-axis is found using the arctangent formula, adjusting for the quadrant the resultant vector lies in.
- 🔄 For vectors in different quadrants, adjust the reference angle by adding or subtracting from 180 or 360 degrees to find the correct direction.
- 📊 The script provides formulas and methods for adding vectors, emphasizing the importance of understanding vector direction and magnitude in relation to each other.
Q & A
What is a vector and how does it differ from a simple quantity?
-A vector is a quantity that has both magnitude and direction, unlike a simple quantity which only has magnitude. For example, a force vector might have a magnitude of 100 newtons and be directed towards the east.
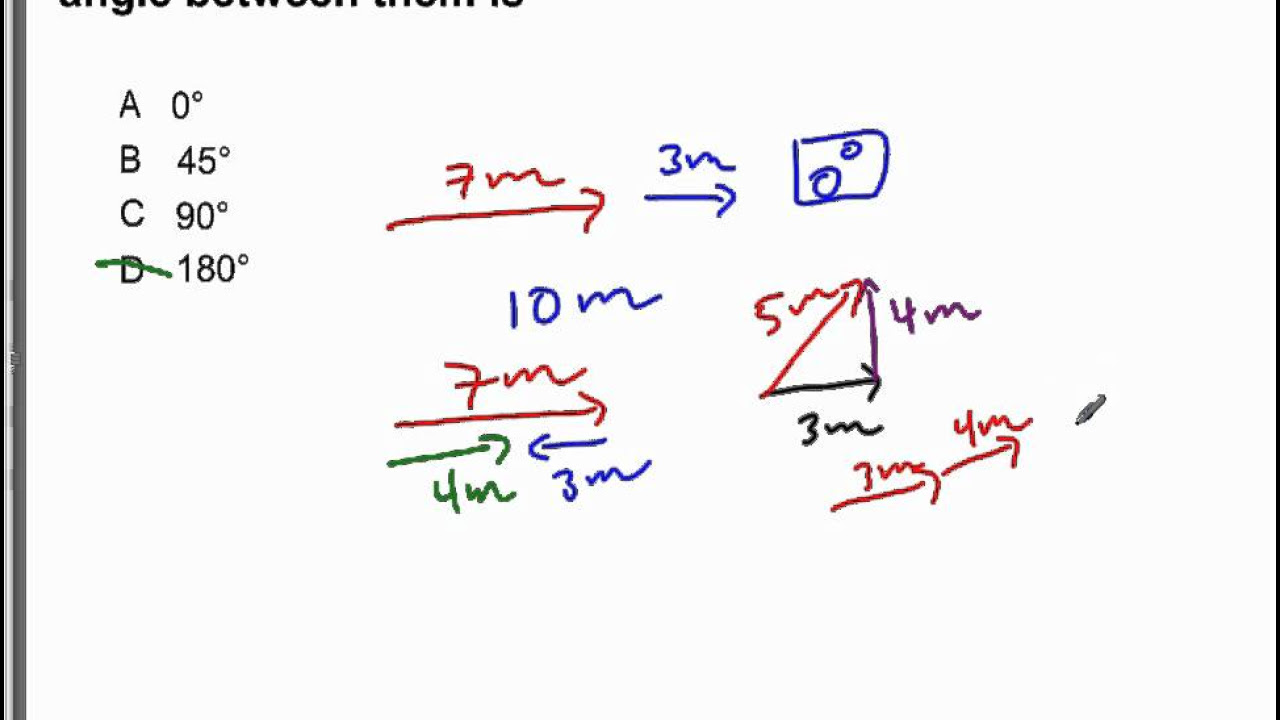
How do you add two vectors that are parallel to each other?
-When two vectors are parallel, you can simply add their magnitudes to get the resultant sum. For instance, if you have two forces of 100 newtons and 50 newtons directed east, their resultant sum would be a net force of 150 newtons.
What is the resultant vector when two vectors are in opposite directions?
-When two vectors are in opposite directions, you subtract the smaller magnitude from the larger one to get the resultant vector. For example, a 200 newton vector directed east and a 120 newton vector directed west would result in a net force of 80 newtons directed east.
How do you calculate the resultant force vector when two forces are perpendicular to each other?
-For two perpendicular forces, you calculate the resultant force vector by finding the square root of the sum of the squares of the individual forces. This is derived from the Pythagorean theorem, as in the example where a 30 newton force and a 40 newton force result in a 50 newton resultant force.
What is the formula to find the angle of the resultant force vector?
-The angle (theta) of the resultant force vector can be found using the arctangent function of the y component divided by the x component, or `tan^(-1)(Fy/Fx)`.
How do you determine the direction of the resultant force vector based on the angle?
-The direction of the resultant force vector is determined relative to the positive x-axis. Depending on the quadrant the resultant force lies in, you adjust the reference angle by adding or subtracting from 180 or 360 degrees as necessary.
What is the magnitude of the resultant force vector when adding a 50 newton force directed west and a 120 newton force directed south?
-The magnitude of the resultant force vector is the square root of the sum of the squares of the two forces, which is `sqrt(50^2 + 120^2)`, resulting in a magnitude of 130 newtons.
How do you find the angle of the resultant force vector when it's in the third quadrant?
-In the third quadrant, the angle of the resultant force vector is found by adding 180 degrees to the reference angle. The reference angle is calculated using the arctangent function of the y component divided by the x component.
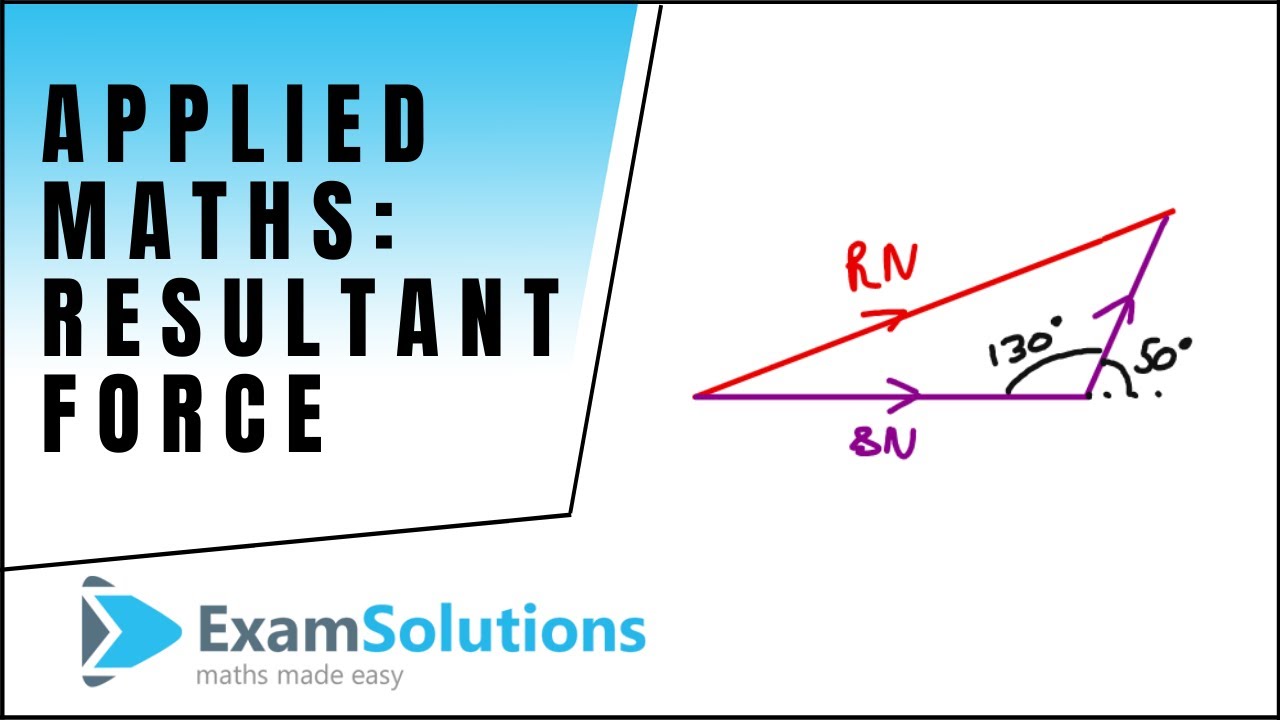
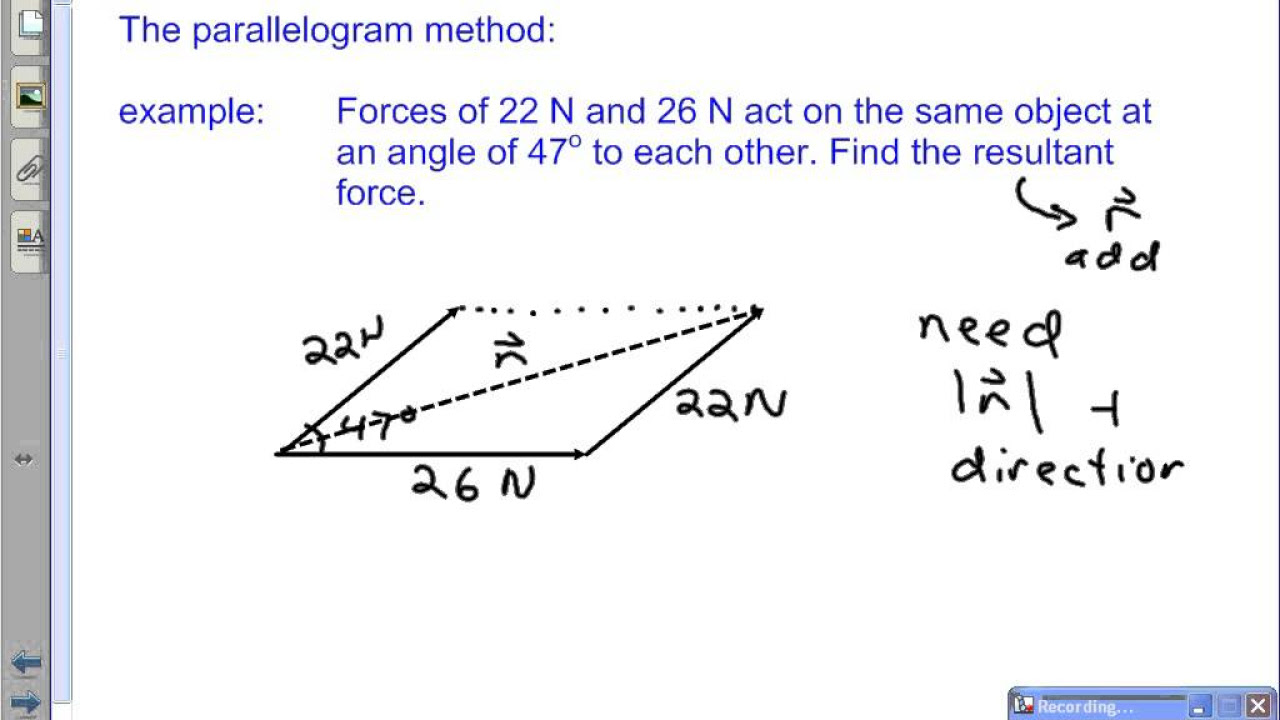
What is the process for adding vectors that are not parallel or perpendicular?
-For vectors that are not parallel or perpendicular, you use the component method. This involves breaking each vector into its x and y components, adding these components separately, and then using the Pythagorean theorem and arctangent function to find the magnitude and direction of the resultant force vector.
How do you calculate the x and y components of a force vector?
-The x component (Fx) of a force vector is calculated as the magnitude of the force multiplied by the cosine of the angle (F*cos(theta)), and the y component (Fy) is the magnitude multiplied by the sine of the angle (F*sin(theta)).
What is the resultant force vector when adding a 100 newton force directed east and a 150 newton force at 30 degrees above the x-axis?
-The resultant force vector is found by adding the x and y components of the two forces and then using the Pythagorean theorem to find the magnitude, which is `sqrt((100 + 129.9)^2 + 75^2)`, resulting in a magnitude of 241.8 newtons. The direction is found using the arctangent function of the y component over the x component, resulting in an angle of 18.1 degrees.
Outlines
📚 Introduction to Vector Addition
This paragraph introduces the concept of vector addition, explaining that a vector is a quantity with both magnitude and direction. It uses the example of force vectors to illustrate how to add vectors that are parallel to each other. The resultant sum of such vectors is found by simply adding their magnitudes. The paragraph also discusses how to handle vectors with opposite directions and introduces the concept of net force, demonstrating this with a vector directed east and another directed west.
🔍 Calculating Resultant Vectors in Different Quadrants
This paragraph delves into the calculation of resultant vectors when the forces are not parallel or anti-parallel. It explains how to find the resultant force vector when two vectors are perpendicular to each other by using the Pythagorean theorem. The paragraph also covers how to find the direction of the resultant force vector by using the inverse tangent function of the y component divided by the x component. The explanation includes examples with different force magnitudes and directions, demonstrating how to calculate the magnitude and direction of the resultant force vector in various scenarios.
📐 Component Method for Non-Perpendicular Vectors
This paragraph introduces the component method for adding vectors that are not parallel or perpendicular. It explains the process of breaking down the vectors into their x and y components, adding these components separately, and then using the Pythagorean theorem to find the magnitude of the resultant force vector. The paragraph provides a step-by-step example of adding a vector directed east with a magnitude of 100 newtons and another vector with a magnitude of 150 newtons at an angle of 30 degrees above the x-axis. It details how to calculate the x and y components for each vector and how to combine them to find the resultant vector's magnitude and direction.
🎯 Final Resultant Vector Calculation
The final paragraph concludes the discussion on vector addition by summarizing the calculations for the resultant vector's magnitude and direction. It confirms the magnitude as 241.8 newtons and the direction as 18.1 degrees, providing a clear and concise summary of the vector addition process described in the previous paragraphs. This paragraph serves as a wrap-up, reinforcing the understanding of the concepts and methods discussed throughout the video script.
Mindmap
Keywords
💡Vector
💡Magnitude
💡Direction
💡Resultant Force
💡Parallel Vectors
💡Perpendicular Vectors
💡Component Method
💡Pythagorean Theorem
💡Angle Theta
💡Tangent
💡Quadrants
Highlights
Vectors are quantities with magnitude and direction, such as force vectors.
The magnitude of a force vector represents the size of the force, like 100 newtons.
The direction of a force vector indicates where the force is applied, e.g., towards the east.
When two vectors are parallel, their magnitudes can be directly added to find the resultant sum.
The resultant vector of two equal and opposite forces can be calculated by subtracting their magnitudes.
For non-parallel vectors, the resultant force vector can be found using the Pythagorean theorem and trigonometric functions.
The magnitude of the resultant force vector is the square root of the sum of the squares of its components.
The direction of the resultant force vector is determined by the arctangent of the y-component divided by the x-component.
The angle of the resultant force vector relative to the x-axis can be found based on the quadrant it lies in.
For vectors not parallel or perpendicular, the component method is used to break them into x and y components.
The x-component of a force vector is calculated by multiplying the force's magnitude with the cosine of its angle.
The y-component of a force vector is calculated by multiplying the force's magnitude with the sine of its angle.
The resultant force vector's magnitude and direction can be visualized by graphing the individual vectors and their components on an xy plane.
The reference angle for a force vector can be found using the arctangent of the y-direction force divided by the x-direction force.
The angle of the resultant force vector in different quadrants is adjusted based on the reference angle and the quadrant it lies in.
The magnitude and direction of the resultant force vector can be used to understand the overall effect of multiple forces acting on an object.
The component method for adding vectors is a fundamental concept in physics and engineering for analyzing forces and motions.
Understanding vector addition is crucial for solving problems in mechanics, aerodynamics, and many other fields of science and technology.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: