How To Find The Resultant of Two Vectors

The Organic Chemistry Tutor
21 Jan 202111:10
EducationalLearning
32 Likes 10 Comments

TLDRThe video script explains the process of calculating the magnitude and direction of a resultant vector formed by the sum of two force vectors. It details breaking down each force vector into its x and y components, using cosine and sine of the angles, and then adding these components together. The script introduces unit vectors and their role in representing the components. Finally, it demonstrates how to find the magnitude and direction of the resultant vector using the Pythagorean theorem and arctangent, resulting in a comprehensive understanding of vector addition and its applications.

Takeaways
  • 📚 The video explains how to calculate the magnitude and direction of the resultant vector from the sum of two force vectors.
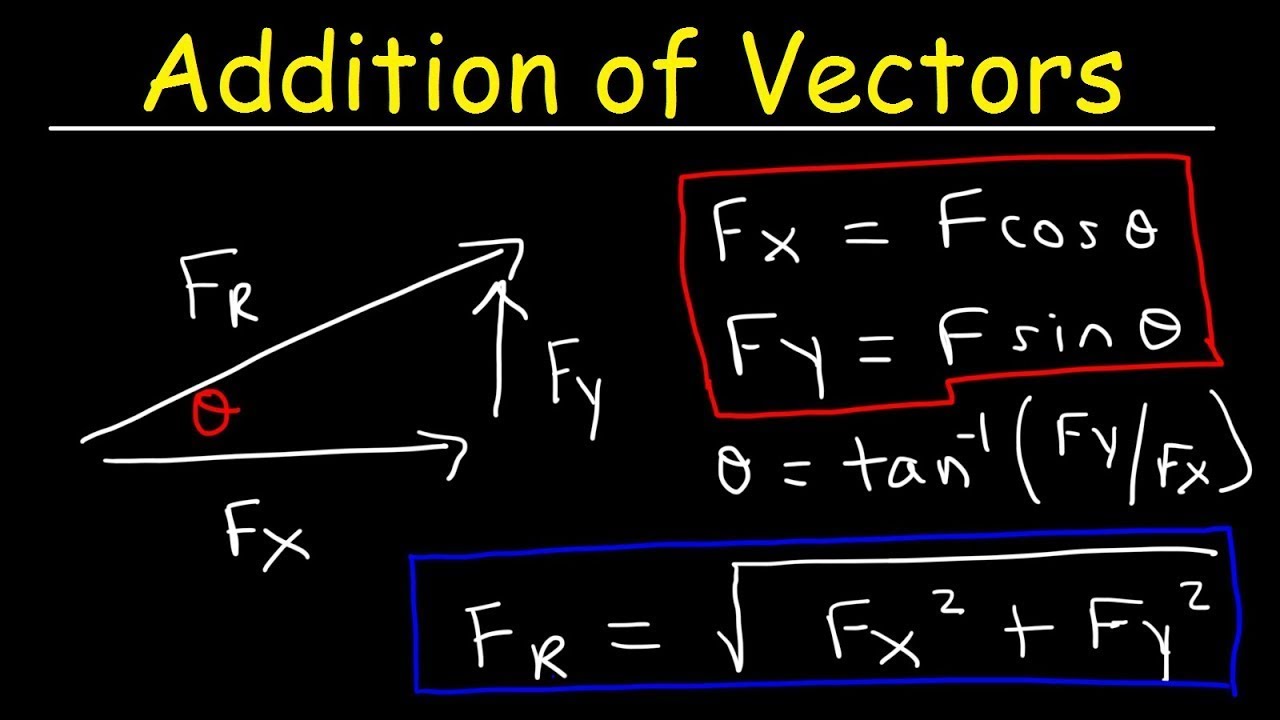
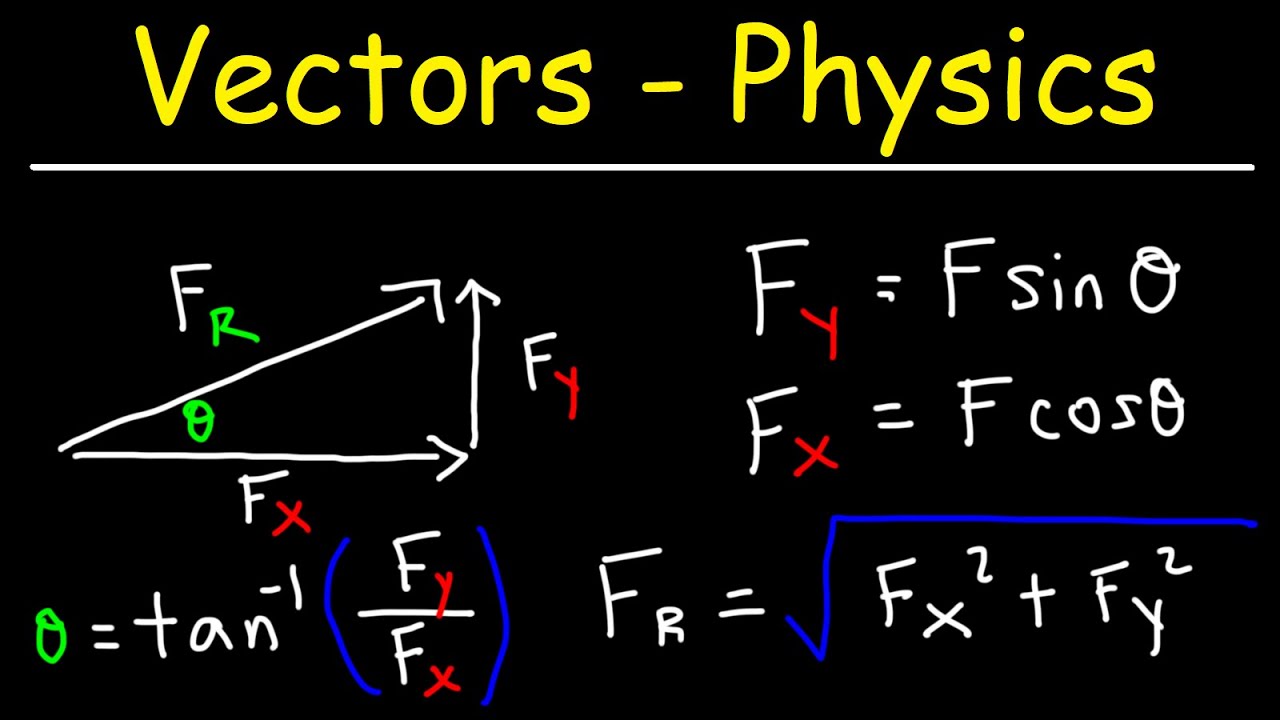
  • 📑 It starts with breaking down each vector into its x and y components, using cosine for x (f1x = f1 cos(theta)) and sine for y (f1y = f1 sin(theta)).
  • 🔬 The x and y components of the first vector (f1) are calculated as 173.2N and 100N, respectively, with f1 having a magnitude of 200N at 30 degrees.
  • 🔭 The second vector (f2) has its components calculated considering an angle of 135 degrees from the positive x-axis, resulting in x and y components of -212.1N and 212.1N, respectively, with f2 having a magnitude of 300N.
  • 📊 Unit vectors 'i' and 'j' represent directions along the x-axis and y-axis, respectively, helping express vector components in a standard form.
  • 📈 The resultant vector is found by adding the corresponding components of f1 and f2, leading to a vector in component form (-38.9i + 312.1j).
  • 💾 To find the magnitude of the resultant vector, the Pythagorean theorem is applied, resulting in a magnitude of 314.5N.
  • 🔮 The direction of the resultant vector is determined by calculating the reference angle from the tangent of the y component over the x component, adjusted to 97.1 degrees from the positive x-axis.
  • 🕖 The video illustrates the process with a graphical representation, plotting the components and resultant vector on a graph.
  • 🌐 The final answer gives the resultant vector a magnitude of 314.5N and a direction of 97.1 degrees counterclockwise from the positive x-axis.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is how to calculate the magnitude and direction of the resultant vector formed by the sum of two other force vectors.

  • What are the two force vectors shown in the diagram?

    -The two force vectors shown in the diagram are F1 and F2, with F1 having a magnitude of 200 newtons at an angle of 30 degrees and F2 having a magnitude of 300 newtons at an angle of 45 degrees relative to the positive x-axis.

  • How is the resultant vector calculated?

    -The resultant vector is calculated by breaking down each force vector into its component form along the x and y axes, then adding the components together to get the resultant vector in component form.

  • What are i and j in the context of the video?

    -In the context of the video, i and j are unit vectors representing the x and y axes, respectively. They are used to express a force vector in its component form.

  • How is the x component of F1 calculated?

    -The x component of F1 is calculated as F1 cosine theta, which is 200 newtons times the cosine of 30 degrees (0.866), resulting in 173.2 newtons.

  • How is the y component of F1 calculated?

    -The y component of F1 is calculated as F1 sine theta, which is 200 newtons times the sine of 30 degrees (0.5), resulting in 100 newtons.

  • What is the angle used for calculating the x component of F2?

    -The angle used for calculating the x component of F2 is 135 degrees, which is the angle relative to the positive x-axis in the second quadrant.

  • What is the magnitude of the resultant vector?

    -The magnitude of the resultant vector is 314.5 newtons, calculated using the Pythagorean theorem on the components of the vector.

  • What is the direction of the resultant vector?

    -The direction of the resultant vector is 97.1 degrees from the positive x-axis, counter-clockwise, as determined by subtracting the reference angle from 180 degrees.

  • How is the reference angle for the resultant vector found?

    -The reference angle for the resultant vector is found by taking the arctangent of the y component divided by the x component, and then subtracting it from 180 degrees to get the angle relative to the positive x-axis.

  • What is the significance of the negative sign in the x component of F2?

    -The negative sign in the x component of F2 indicates that the force is in the second quadrant where x values are negative on the Cartesian coordinate system.

Outlines
00:00
📏 Calculating Resultant Vector Magnitude and Direction

This paragraph introduces the process of calculating the magnitude and direction of a resultant vector formed by the sum of two force vectors. It explains the need to break down each vector into its component form and then add the components together to obtain the resultant vector's components. The paragraph details the calculation of the x and y components for the first force vector (f1), using trigonometric functions and providing the values for f1 in component form as 173.2i + 100j. It also introduces the concept of unit vectors i and j, which are along the x-axis and y-axis respectively, and are used to express a force vector in component form.

05:02
🔢 Component Form and Addition of Force Vectors

The second paragraph continues the explanation of calculating force vectors by determining the x and y components for the second force vector (f2). It explains the use of the reference angle and how to find the angle relative to the positive x-axis for the second force vector. The paragraph provides the calculation for f2 in component form as -212.1i + 212.1j. It then describes how to add the components of f1 and f2 to obtain the resultant vector in component form, which is -38.9i + 312.1j. The paragraph also discusses the next step, which is to draw a graph to visually represent the components and calculate the magnitude and direction of the resultant vector.

10:03
📐 Finding Magnitude and Direction of the Resultant Vector

The final paragraph concludes the process by explaining how to find the magnitude and direction of the resultant vector. It describes the use of the Pythagorean theorem to calculate the magnitude, which is found to be 314.5 newtons. The paragraph also explains how to calculate the direction of the resultant vector by finding the reference angle and then determining the angle relative to the positive x-axis, which is 97.1 degrees counter-clockwise. The paragraph provides a comprehensive summary of the entire process, emphasizing the magnitude and direction of the resultant vector as the key outcomes.

Mindmap
Keywords
💡magnitude
The term 'magnitude' in the context of the video refers to the size or strength of a vector, specifically the resultant vector formed by the sum of two force vectors. It is a crucial concept in vector analysis as it quantifies the overall effect of the combined forces. The magnitude of the resultant vector is calculated using the Pythagorean theorem, as demonstrated in the video by finding the hypotenuse of the right triangle formed by the x and y components of the vectors.
💡direction
The 'direction' of a vector is the angle it makes with a reference axis, typically the positive x-axis. In the video, the direction of the resultant vector is determined by calculating the angle counter-clockwise from the positive x-axis, which is found to be 97.1 degrees. Understanding direction is essential in vector analysis as it provides information on the orientation of the force in the context of the problem.
💡resultant vector
A 'resultant vector' is the single vector that represents the combined effect of two or more vectors. In the video, the resultant vector is derived by adding the x and y components of two force vectors, f1 and f2. The resultant vector is a fundamental concept in physics and engineering, as it simplifies the analysis of multiple forces acting at a point.
💡force vectors
In the context of the video, 'force vectors' are vectors that represent physical forces with both magnitude and direction. They are used to analyze the effect of different forces acting on an object. Each force vector is decomposed into its x and y components, which are then combined to find the resultant vector.
💡components
The term 'components' in the video refers to the individual x and y parts of a vector. Breaking down a force vector into its components allows for the application of vector addition rules in the Cartesian coordinate system. These components are the fundamental building blocks used to calculate the resultant vector.
💡unit vectors
Unit vectors, denoted as 'i' and 'j' in the video, are vectors with a magnitude of one that point along the x-axis and y-axis of a Cartesian coordinate system, respectively. They are used to express the components of a vector in terms of their direction along these axes. The concept of unit vectors is essential for performing vector calculations in two-dimensional space.
💡cosine and sine
The 'cosine' and 'sine' are trigonometric functions used to relate the angles and sides of a right triangle. In the context of the video, cosine and sine are used to calculate the x and y components of the force vectors. Cosine of an angle gives the ratio of the adjacent side to the hypotenuse, while sine gives the ratio of the opposite side to the hypotenuse.
💡Pythagorean theorem
The 'Pythagorean theorem' is a fundamental principle in geometry that states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. In the video, this theorem is used to calculate the magnitude of the resultant vector by finding the hypotenuse of the right triangle formed by the x and y components.
💡arctangent
The 'arctangent' function, often written as tan^(-1) or atan, is the inverse function of the tangent and is used to find the angle whose tangent is a given value. In the video, arctangent is used to determine the reference angle from the ratio of the y component to the x component of the resultant vector, which is a step towards finding the direction of the resultant vector.
💡reference angle
A 'reference angle' is the acute angle (less than 90 degrees) formed by a line segment from the origin to a point on a unit circle and the positive x-axis. In the context of the video, the reference angle is used as an intermediate step to find the final direction of the resultant vector relative to the positive x-axis.
💡counter-clockwise
In the context of the video, 'counter-clockwise' refers to the direction in which the angle is measured when moving from the positive x-axis in a leftward direction around the origin in a Cartesian coordinate system. This term is used to describe the direction of the resultant vector relative to the positive x-axis.
Highlights

The video discusses the method to calculate the magnitude and direction of the resultant vector formed by the sum of two force vectors.

Each force vector must be broken down into its component form to find the resultant vector.

The x component of a force vector is calculated using the cosine of the angle.

The y component of a force vector is calculated using the sine of the angle.

Unit vectors 'i' and 'j' represent the directions along the x-axis and y-axis respectively.

The component form of the first force vector f1 is 173.2 i + 100 j.

The second force vector f2 has an x component calculated with a cosine of 135 degrees and a y component with a sine of 135 degrees.

The x component of f2 is negative, indicating its direction in the second quadrant.

The y component of f2 is positive, as it is above the x-axis in the second quadrant.

The resultant vector in component form is the sum of the x and y components of f1 and f2.

The magnitude of the resultant vector is found by calculating the hypotenuse of the right triangle formed by the x and y components.

The Pythagorean theorem is used to calculate the magnitude of the resultant vector.

The direction of the resultant vector is determined by the angle it makes with the positive x-axis, found using the arctangent function.

The final resultant vector has a magnitude of 314.5 newtons and a direction of 97.1 degrees from the positive x-axis, counter-clockwise.

The process demonstrated is essential for understanding vector addition and its applications in physics.

The method can be applied to various real-world scenarios involving the summation of forces.

The video provides a clear and detailed explanation of the vector addition process, making it accessible to a wide audience.

Transcripts

Browse More Related Video

AP Physics B Kinematics Presentation #68

AP Physics B Kinematics Presentation General Problems #08

Vectors Full Topic -Physics

Adding Vector Components | Physics with Professor Matt Anderson | M3-07

Addition of Vectors By Means of Components - Physics

Vectors - Basic Introduction - Physics

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Vector CalculusPhysics TutorialComponent AnalysisMathematics ApplicationForce VectorsResultant VectorPythagorean TheoremEducational ContentProblem SolvingEngineering Concepts