Vectors - Precalculus
TLDRThis video script delves into the concept of vectors, differentiating them from scalar quantities by highlighting that vectors possess both magnitude and direction. It uses examples such as force and velocity to illustrate vector properties and provides a step-by-step guide on how to express vectors in terms of their i, j components and calculate their magnitudes using the Pythagorean theorem. The script further explains how to find terminal points given initial points and vector components, and introduces three-dimensional vectors with corresponding components. It also touches on how to determine the angle a vector makes with the positive x-axis using trigonometric principles.
Takeaways
- 💡 Scalar quantities have magnitude only, while vector quantities have both magnitude and direction.
- 💡 Examples of scalar quantities include mass, speed, and temperature; examples of vector quantities include force, velocity, and acceleration.
- 💡 Mass cannot be directed towards a point (e.g., '30 kilograms directed east' makes no sense), illustrating the nature of scalar quantities.
- 💡 Force is an example of a vector quantity because it involves both magnitude (how much force) and direction (where it's applied).
- 💡 Vector quantities can be represented in component form (i.e., x and y components in a plane), simplifying calculations and representations.
- 💡 The magnitude of a vector can be calculated using the Pythagorean theorem, representing the length of the vector in space.
- 💡 When moving from an initial point to a terminal point in space, the change in x and y coordinates (delta x and delta y) represent the vector components.
- 💡 The magnitude of vectors is calculated using the square root of the sum of the squared components, which comes from the Pythagorean theorem.
- 💡 To find a terminal point given an initial point and a vector, you add the vector's components to the initial point's coordinates.
- 💡 In three-dimensional space, vectors include a z-component and are represented with i, j, and k components, with magnitude calculation extending to include the z-component.
Q & A
What is the primary difference between a scalar and a vector quantity?
-A scalar quantity has only magnitude, while a vector quantity has both magnitude and direction.
Can you provide an example of a scalar quantity and explain why it is considered scalar?
-Mass is an example of a scalar quantity because it has magnitude but no inherent direction associated with it.
How is force different from mass in terms of scalar and vector properties?
-Force is a vector quantity because it has both magnitude and direction, allowing us to specify, for example, a force of 200 Newtons directed east.
What are the components of a vector and how are they determined?
-The components of a vector are its i (x) and j (y) parts, determined by the differences in the respective coordinates of the initial and terminal points.
How do you calculate the magnitude of a vector?
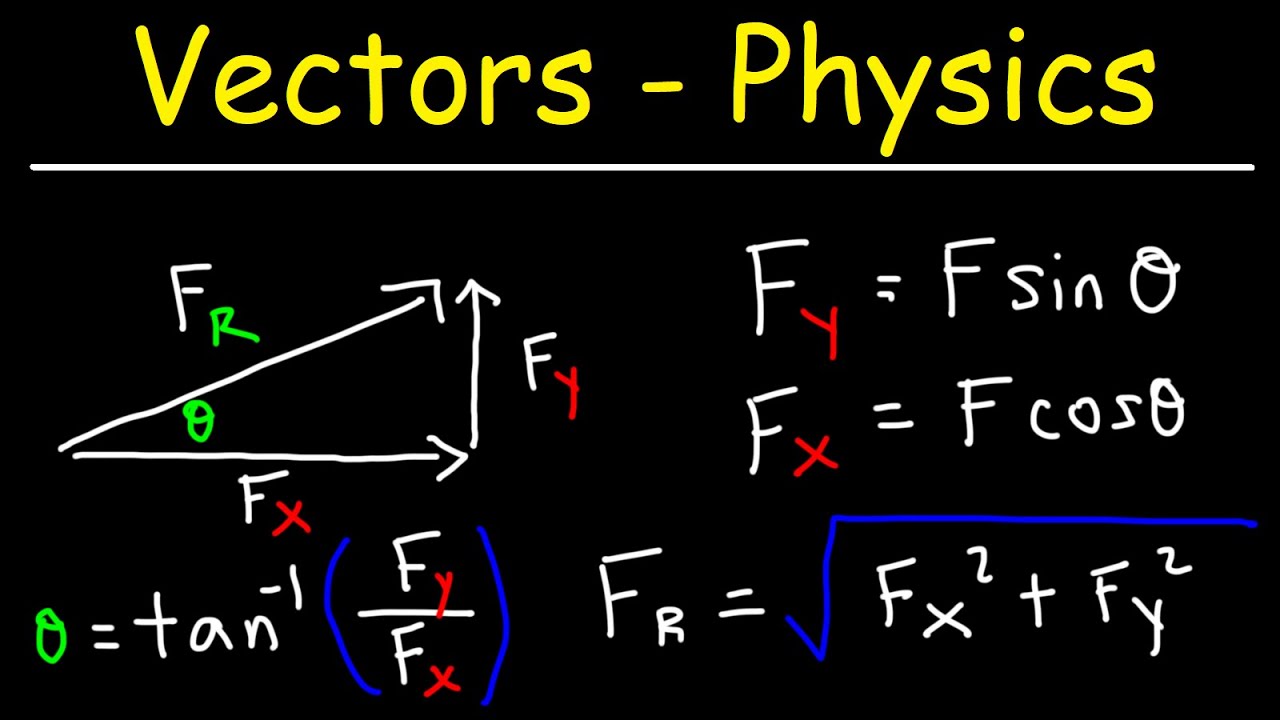
-The magnitude of a vector is calculated using the Pythagorean theorem: √(v_x^2 + v_y^2), where v_x and v_y are the components of the vector along the x and y axes.
Given two points A and B with coordinates (1, 2) and (4, 6), how would you express the vector from A to B and find its magnitude?
-The vector from A to B is expressed as 3i + 4j, and its magnitude is calculated as √(3^2 + 4^2) = √(9 + 16) = √25 = 5.
If the initial point A is at (-4, -5) and the vector v is 5i + 12j, how do you find the terminal point B?
-By adding the vector components to the initial point's coordinates: x2 = -4 + 5 = 1, y2 = -5 + 12 = 7, so point B is at (1, 7).
What is the formula to find the terminal point B given an initial point A and a vector v?
-The terminal point B can be found using the formula: B(x2, y2) = A(x1) + v_x * i + v_y * j.
How do you find the vector components and magnitude for a 3D vector given the initial and terminal points with x, y, and z coordinates?
-The vector components are found by subtracting the initial point's coordinates from the terminal point's coordinates (x2 - x1, y2 - y1, z2 - z1). The magnitude is calculated as √((x2 - x1)^2 + (y2 - y1)^2 + (z2 - z1)^2).
Given the vector v as 4i + 6j, how do you find its magnitude and the angle it makes with the positive x-axis?
-The magnitude of v is √(4^2 + 6^2) = √(16 + 36) = √52 = 2√13. The angle with the positive x-axis is found using the arctangent function: θ = arctan( Vy / Vx ) = arctan( 6 / 4 ) ≈ 56.3 degrees.
What is the significance of understanding both the magnitude and direction of a vector?
-Understanding both the magnitude and direction of a vector is crucial as it allows for a complete description of the vector's behavior in space, which is essential in fields such as physics, engineering, and computer graphics.
In the context of physics, why is it important to differentiate between scalar and vector quantities?
-Differentiating between scalar and vector quantities is important because scalars only convey information about size or quantity, while vectors provide complete information about both size and direction, which is necessary for accurate physical modeling and problem-solving.
Outlines
📏 Understanding Scalars and Vectors
This paragraph introduces the concepts of scalar and vector quantities. It explains that scalar quantities, such as mass, have only magnitude without direction, while vector quantities, like force, have both magnitude and direction. The example of mass versus force clarifies the difference, with mass being a scalar (30 kg) and force being a vector (200 N east). The paragraph also introduces the concept of representing vectors in terms of their components and calculating the magnitude of a vector using the Pythagorean theorem.
📐 Calculating Vector Components and Magnitude
The second paragraph delves into the process of expressing vectors in terms of their i and j components and calculating their magnitudes. It provides a step-by-step explanation of how to find the components by taking the difference in x and y values between two points. The magnitude of a vector is found using the equation derived from the Pythagorean theorem, with examples given to illustrate the process. The paragraph also touches on graphing vectors and finding the terminal point of a vector.
🔍 Finding Terminal Points Using Vectors
This paragraph focuses on using vector components to determine the terminal point of a vector given the initial point. It explains how to graphically plot the initial point and use the vector components to find the terminal point's coordinates. The process involves adding the x and y components to the initial point's coordinates. The paragraph reinforces the concept with examples and provides a clear method for solving such problems.
📊 Three-Dimensional Vectors and Angle Calculation
The fourth paragraph extends the vector concept to three dimensions, explaining how to find the vector components in the x, y, and z directions and calculate the vector's magnitude using the three squared components. It also introduces the concept of finding the angle a vector makes with the positive x-axis using trigonometric relationships and the inverse tangent function. The paragraph provides a comprehensive explanation with examples, illustrating the process of dealing with three-dimensional vectors and their angles.
Mindmap
Keywords
💡Scalars
💡Vectors
💡Magnitude
💡Direction
💡Components
💡Acceleration
💡Velocity
💡Graphing
💡Pythagorean Theorem
💡Terminal Point
💡Inverse Tangent
Highlights
Scalars have only magnitude, whereas vector quantities have both magnitude and direction.
Mass is a scalar quantity, and force is a vector quantity.
The directed line segment from point A to point B can represent a vector.
Vector components can be expressed in terms of i and j for 2D vectors.
The magnitude of a vector can be found using the Pythagorean theorem.
Vector magnitude is calculated as the square root of the sum of squared components.
To find the terminal point B given an initial point A and a vector, simply add the vector components to the initial point's coordinates.
In 3D space, vectors are expressed with i, j, and k components.
The magnitude of a 3D vector is found using the square root of the sum of the squares of its i, j, and k components.
The angle of a vector relative to the positive x-axis can be found using the tangent of the y component divided by the x component.
The angle above the positive x-axis can be calculated using the inverse tangent function.
Velocity and acceleration are examples of vector quantities, while speed and temperature are scalar quantities.
To express a vector in component form, subtract the initial point's coordinates from the terminal point's coordinates.
Graphing the vector components on a coordinate system can visually represent the vector and its magnitude.
For a 2D vector, the direction can be specified by the angle it makes with the x-axis.
The concept of vectors is fundamental in fields such as physics and engineering for describing motion and forces.
Understanding vector operations is crucial for solving problems in mechanics and other technical applications.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: