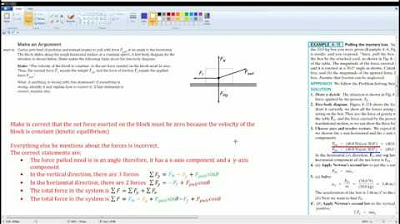
AP Physics Workbook 2.F Direction of Friction

Mr.S ClassRoom
22 Apr 202007:00
EducationalLearning
32 Likes 10 Comments

TLDRThis video script discusses the dynamics of a bulldozer pushing a cement cube on a rough surface, focusing on the forces involved and their directions. It guides through drawing Freebody diagrams to visualize the forces acting on both the bulldozer and the cube, including gravity, normal force, and friction. The script then applies Newton's second law to set up equations for the system, demonstrating how to calculate the acceleration of the bulldozer and the cube. The example uses given forces and masses to derive the system's acceleration, showcasing a practical application of physics principles.

Takeaways
  • 📚 The scenario involves a bulldozer of mass M pushing a cube of cement of mass m across a rough surface, causing both to speed up.
  • 🔢 Four forces act on the bulldozer: gravity (downward), normal force (upward), forward thrust (left), and friction (right).
  • 🎨 A Freebody diagram is used to represent these forces visually, showing the direction and relative magnitude of each.
  • 🚜 The bulldozer experiences a forward force due to the ground and a backward force due to the cube's friction.
  • 🔄 Newton's third law is evident as the forces exerted by the bulldozer on the cube and vice versa cancel each other out.
  • 📐 When analyzing the system as a whole, the combined force from the ground on the bulldozer minus the combined frictional force equals the total mass times the acceleration (F = (M+m)a).
  • 🧮 The problem provides specific values: the forward force is 5000 Newtons, the frictional force is 2000 Newtons, M is 1000 kg, and m is 500 kg.
  • 🔢 By substituting the given values into the equation, the acceleration of the system can be calculated as 2 m/s².
  • 📈 The key to solving the problem lies in correctly applying Newton's second law and understanding the interactions between the bulldozer and the cube.
  • 📝 The final acceleration is the same for both the bulldozer and the cube since they are a single system in this context.
  • 🔍 The process demonstrates the importance of breaking down complex physical situations into manageable parts and solving them systematically.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is the dynamics of a bulldozer pushing a cube of cement across a rough surface, specifically focusing on the forces involved and the direction of friction.

  • What are the four forces acting on the bulldozer?

    -The four forces acting on the bulldozer are gravity (downward), normal force (upward), the force pushing it forward (leftward), and the force pushing it back (rightward due to the cube's resistance).

  • How does the bulldozer and the cube speed up according to the scenario?

    -The bulldozer and the cube speed up because the net force acting on the system is in the forward direction, overcoming the frictional force and resulting in acceleration.

  • What is the significance of the free body diagram in this context?

    -The free body diagram is significant as it helps visualize and analyze all the individual forces acting on the bulldozer and the cube separately, which is essential for solving the dynamics problem.

  • How are the forces on the bulldozer and the cube related according to Newton's third law?

    -According to Newton's third law, the force exerted by the cube on the bulldozer is equal in magnitude and opposite in direction to the force exerted by the bulldozer on the cube. These forces cancel each other out when considering the system as a whole.

  • What are the two equations based on Newton's second law that need to be set up?

    -The two equations based on Newton's second law are: 1) For the bulldozer: F Bulldozer (forward) - F Cube (backward) = (M + m) * a, and 2) For the cube: F Bulldozer (forward) - F Friction = m * a.

  • How is the acceleration of the system derived in the video?

    -The acceleration of the system is derived by combining the two separate equations for the bulldozer and the cube, and then solving for 'a' using the given values of the forces and masses involved.

  • What is the final acceleration of the bulldozer and the cube system?

    -The final acceleration of the bulldozer and the cube system is 2 meters per second squared, represented as 'a'.

  • How does the force of friction affect the system?

    -The force of friction opposes the motion of the system. It is a resistive force that must be overcome by the applied force (from the bulldozer) for the system to accelerate.

  • What are the units for the force of gravity and the force of friction as mentioned in the video?

    -The units for the force of gravity and the force of friction mentioned in the video are Newtons (N).

  • What is the combined mass of the bulldozer and the cube?

    -The combined mass of the bulldozer (M = 1000 kg) and the cube (m = 500 kg) is 1500 kg.

Outlines
00:00
📚 Introduction to Dynamics and Freebody Diagrams

This paragraph introduces the topic of dynamics within the AP Physics workbook, focusing on the concept of friction. The scenario involves a bulldozer of mass M pushing a cube of cement with mass m across a rough surface, causing both to speed up. The task is to represent the forces acting on the bulldozer by drawing a Freebody diagram, which includes gravity, normal force, and the forces to the left and right (friction and pushing force). It explains the forces acting on both the bulldozer and the cube, and how they should be represented in the diagram, including the cancellation of forces due to Newton's third law.

05:02
🧮 Setting up Equations Based on Newton's Second Law

The second paragraph delves into the application of Newton's second law to the scenario described. It guides through setting up equations for both the bulldozer and the cube, considering the forces acting on them individually and combined. The explanation covers how to derive the acceleration of the system by combining the equations and accounting for the cancellation of certain forces. The paragraph concludes with a step-by-step calculation to find the acceleration, given the force on the ground, the mass of the bulldozer and the cube, and the force of friction. The final result is presented, indicating the acceleration in meters per second squared.

Mindmap
Keywords
💡Freebody diagram
A freebody diagram is a graphical representation that shows all the forces acting on an object when it is in equilibrium or motion. In the video, the freebody diagram is used to visualize the forces acting on the bulldozer and the cube of cement, which include gravity, normal force, and friction. This tool is essential for analyzing the dynamics of the system and setting up the equations needed to solve for acceleration.
💡Friction
Friction is the resistive force that opposes the relative motion or tendency of such motion of two surfaces in contact. In the context of the video, friction is a key force that acts on both the bulldozer and the cube of cement as they move across the rough surface. The force of friction is essential to consider when calculating the acceleration of the system, as it opposes the forward motion and affects the overall dynamics.
💡Newton's second law
Newton's second law of motion states that the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass. It is mathematically expressed as F = ma, where F is the net force, m is the mass, and a is the acceleration. In the video, Newton's second law is used to set up equations for the bulldozer and the cube to determine their accelerations.
💡Acceleration
Acceleration is the rate of change of velocity of an object with respect to time. It is a vector quantity that describes how quickly an object speeds up, slows down, or changes direction. In the video, the goal is to derive the acceleration of the bulldozer and the cube system as they move across the surface. This is achieved by analyzing the forces acting on the system and applying Newton's second law.
💡Mass
Mass is a measure of the amount of matter in an object, typically measured in kilograms. It is a fundamental property that affects an object's inertia and the gravitational force it experiences. In the video, the masses of the bulldozer (M) and the cube (m) are crucial parameters used in the equations to determine the system's acceleration.
💡Force
Force is any action that, when unopposed, will change the motion of an object. It can be contact or non-contact and is measured in Newtons (N). In the video, various forces are discussed, including gravity, normal force, and friction, all of which contribute to the dynamics of the bulldozer and the cube.
💡Bulldozer
A bulldozer is a large, powerful vehicle with a wide, flat blade used for pushing soil, debris, or other materials during construction or excavation work. In the video, the bulldozer is the main subject that is pushing a cube of cement, and its interaction with the cube is central to the physics problem being solved.
💡Cube of cement
A cube of cement refers to a solid block of cement, which is a building material often used in construction projects. In the video, the cube is being pushed by a bulldozer, and its mass and the forces acting on it are important for understanding the dynamics of the interaction with the bulldozer.
💡Gravity
Gravity is the force that attracts two bodies towards each other, the force that gives weight to physical objects and causes them to fall towards the Earth when dropped. In the video, gravity is one of the fundamental forces considered in the analysis of the bulldozer and the cube's motion.
💡Normal force
The normal force is the force exerted by a surface as it supports the weight of an object resting on it. It acts perpendicular to the surface. In the video, the normal force acts upwards against gravity for both the bulldozer and the cube, balancing the gravitational pull and playing a role in their motion.
💡System
In physics, a system is a set of interacting objects or entities that are considered as a whole for the purpose of study. In the video, the system consists of the bulldozer and the cube of cement, and the analysis focuses on understanding the dynamics of this combined system.
Highlights

The scenario involves a bulldozer pushing a cube of cement across a rough surface, causing both to speed up.

Four forces act on the bulldozer: gravity downward, normal force upward, and two horizontal forces (one pushing forward and one pushing backward due to friction).

The force of the bulldozer pushing the cube and the force of the cube pushing back on the bulldozer are equal in magnitude and opposite in direction due to Newton's third law.

The net force causing the bulldozer to move forward is the difference between the force exerted by the ground on the bulldozer and the force of friction.

The cube experiences a similar set of forces, but with the force of the bulldozer on the cube being the applied force and friction acting in the opposite direction.

When considering the system as a whole, the internal forces between the bulldozer and the cube cancel each other out, leaving only the external forces to be considered.

The problem can be solved by applying Newton's second law, which states that the net force on an object is equal to the mass of the object multiplied by its acceleration (F = ma).

The forward motion is considered positive, and the backward motion is considered negative when applying Newton's second law to this scenario.

The equation for the bulldozer's acceleration involves the force exerted by the ground minus the force of friction, all divided by the total mass of the bulldozer and the cube.

The force of the ground on the bulldozer is given as 5000 Newtons, and the force of friction is given as 2000 Newtons.

The total mass of the system is the sum of the bulldozer's mass (1000 kg) and the cube's mass (500 kg).

By solving the equation, the acceleration of the system is found to be 2 meters per second squared.

The solution process involves simplifying the equations and understanding the cancellation of internal forces to focus on the external forces affecting the system.

This problem demonstrates the application of Newton's laws of motion to real-world scenarios involving multiple objects and forces.

The concept of free body diagrams is introduced as a tool to visualize and analyze the forces acting on individual objects.

The importance of correctly identifying and representing the forces involved is emphasized for accurate problem-solving.

The solution requires a combination of algebraic manipulation and physical understanding of the forces and their effects.

Transcripts

Browse More Related Video

The Basic Atwood Machine With Friction

AP Physics 1 Dynamics Review

AP Physics Workbook 2.D Newton's Third Law and Eliminating Internal Forces

AP Physics 1 - Elevators

AP Physics Workbook 2.J Modified Atwood Machines

AP Physics Workbook 2.C Force

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
PhysicsWorkbookDynamicsAnalysisFrictionForceBulldozerModelAccelerationEquationAPEducationMechanicalEngineeringProblemSolvingNewtonsLawsEducationalContent