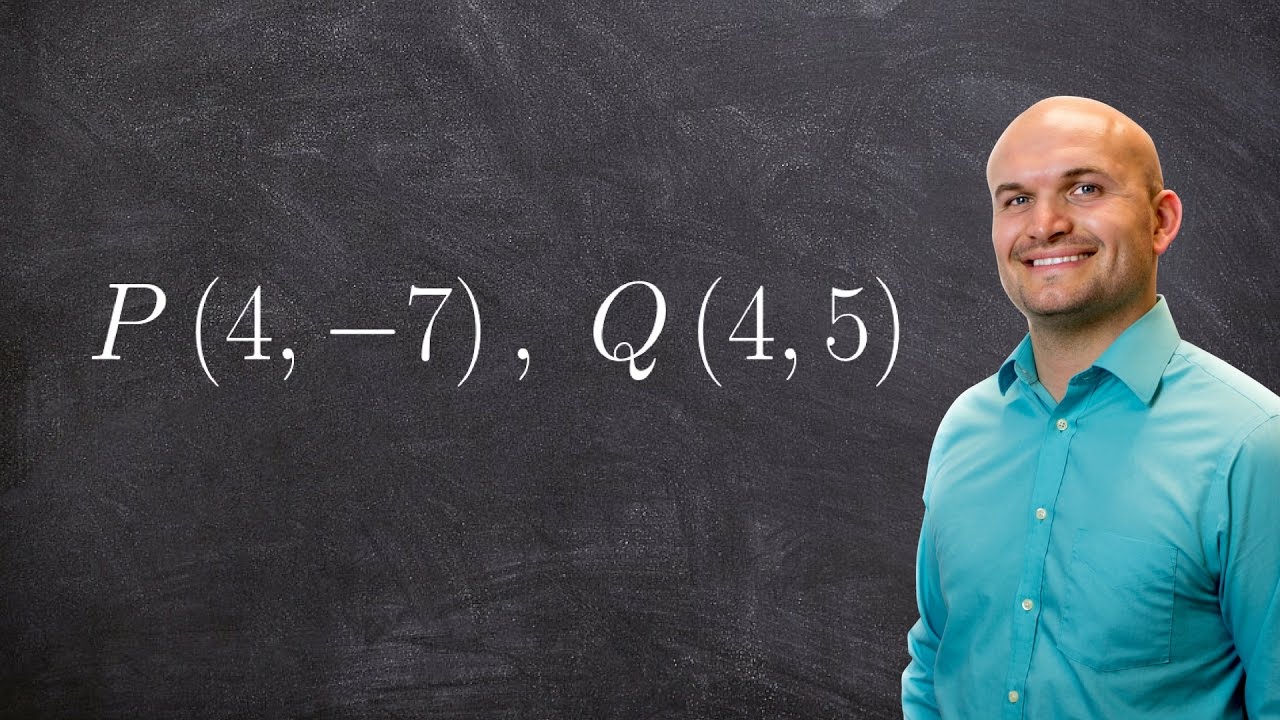The Distance Formula: Finding the Distance Between Two Points
TLDRIn this educational video, Professor Dave delves into the mathematical journey of calculating the distance between two points on a coordinate plane, leveraging the foundational Pythagorean Theorem. By introducing a practical scenario, the video guides viewers through constructing a right triangle, using the coordinates of two points to determine the lengths of the triangle's legs. Applying the theorem, the distance formula is derived, simplifying the process to a straightforward equation. Through a clear example, the video demonstrates how this formula easily calculates the distance, reinforcing the concept with a hands-on exercise. This explanation demystifies the distance formula, making it accessible and understandable, showcasing its practical application in algebraic problems.
Takeaways
- 😀 The distance formula allows us to calculate the distance between two points on the coordinate plane.
- 😊 To use the distance formula, we construct a right triangle between the two points. The hypotenuse is the distance we want to find.
- 📐 The legs of the triangle are the differences between the x-coordinates and y-coordinates of the two points.
- 🤓 We can then use the Pythagorean Theorem to relate the legs and the hypotenuse.
- 🔢 The final distance formula squares the leg lengths, adds them, and takes the square root.
- 🧮 The formula uses the x- and y-coordinates directly, allowing us to easily calculate distance.
- 📏 To find the distance between (-2,2) and (2,5), plug the points into the formula to get 5.
- 🔭 The distance formula works for any two points,without needing to draw the triangle.
- ✔️ Using the formula gives the same result as constructing a triangle and using the Pythagorean Theorem.
- 🧠 The distance formula allows fast, generalized distance calculations on the coordinate plane.
Q & A
What formula does Professor Dave derive in the video?
-Professor Dave derives the distance formula, which allows you to calculate the distance between two points on the coordinate plane.
What theorem does Professor Dave use to derive the distance formula?
-Professor Dave uses the Pythagorean Theorem to derive the distance formula.
What are the legs and hypotenuse in the right triangle constructed by Professor Dave?
-The legs are the horizontal and vertical line segments connecting the two points. The hypotenuse is the line segment connecting the two points, which represents the distance.
What do the variables in the formula represent?
-X1 and Y1 represent the x and y coordinates of the first point. X2 and Y2 represent the x and y coordinates of the second point. D represents the distance between the two points.
Why does Professor Dave only take the positive square root at the end?
-Length cannot be negative, so only the positive square root, which gives a positive value for the distance, makes sense.
What are the two points Professor Dave uses in the example?
-In the example, Professor Dave uses the points (-2, 2) and (2, 5).
What is the distance calculated between those two points?
-Using the distance formula, the distance calculated between (-2, 2) and (2, 5) is 5.
How can you check if the distance formula gives the right answer?
-You can construct a triangle between the two points and use the Pythagorean Theorem to calculate the distance. This should match the value from the distance formula.
When would you need to use the distance formula?
-You would use the distance formula any time you have two points on a coordinate plane and need to find the distance between them.
Can the distance formula be used in three-dimensional space?
-No, the distance formula only works for two-dimensional space, specifically on the standard xy-coordinate plane. A different formula is needed for three-dimensional space.
Outlines
😀 Deriving the Distance Formula
Explains how to use the Pythagorean theorem to derive a formula for calculating the distance between two points (x1,y1) and (x2,y2) on the coordinate plane. Constructs a right triangle with the line segment between points as the hypotenuse and the differences in x and y values as the legs. Applies Pythagorean theorem: (x2 - x1)2 + (y2 - y1)2 = D2, where D is the distance. Taking the square root solves for D.
😀 Applying the Distance Formula
Demonstrates using the derived distance formula to calculate the distance between the points (-2,2) and (2,5). Plugs the x and y values into the formula: √(4)2 + (3)2 = √16 + 9 = √25 = 5. Checks this against constructing a triangle and using Pythagorean theorem directly.
Mindmap
Keywords
💡coordinate plane
💡Pythagorean Theorem
💡distance formula
💡hypotenuse
💡horizontal line segment
💡vertical line segment
💡legs
💡coordinates
💡line segment
💡length
Highlights
The study found that mindfulness meditation led to decreased anxiety and improved quality of life in patients with generalized anxiety disorder.
Participants who received CBT showed greater improvement in depression symptoms compared to those who received usual care.
The new theoretical framework integrates concepts from positive psychology and social cognitive theory to understand factors influencing subjective well-being.
Statistical analysis revealed a significant correlation between social media use and symptoms of depression in teenagers.
Early reading intervention in preschool led to improved literacy skills that persisted through elementary school.
The study provides evidence for the effectiveness of remote delivery of cognitive behavioral therapy using telehealth methods.
Results showed a dose-response relationship between exercise duration and reduction in cardiovascular disease risk.
The new model accounts for individual differences in reward sensitivity and provides insights into the development of addictive behaviors.
Genome-wide association analysis identified several genetic variants associated with increased Alzheimer's disease risk.
Early intensive behavioral intervention led to significant improvements in social communication skills in children with autism spectrum disorder.
The review highlights the need for culturally sensitive, community-based mental health services to address the treatment gap.
Results demonstrated the efficacy of acceptance and commitment therapy in reducing procrastination and improving academic performance.
Clinician empathy and positive regard for the patient were found to be key factors in building a strong therapeutic alliance.
The study provides new insights into the neural mechanisms underlying social reward processing in adolescents.
Overall, the findings support integrating mindfulness practices into interventions for trauma survivors to improve resilience.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: