AP Physics Workbook 2.C Force

Mr.S ClassRoom
22 Apr 202009:23
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses a physics problem involving a block on a horizontal surface, subjected to various forces. It introduces the four basic forces: gravitational, normal, friction, and applied force. The problem is solved by applying Newton's second law and analyzing the forces in both vertical and horizontal directions. The script clarifies common misconceptions and emphasizes the importance of breaking down forces into their X and Y components to solve for acceleration and the normal force accurately.

Takeaways
  • 📚 The script is a tutorial for Unit 2 Dynamics in an AP Physics workbook, focusing on forces and their applications.
  • 🔢 Four basic forces are discussed: normal force (F_N), gravitational force (F_G), frictional force (F_f), and the applied force (F_A).
  • 🎯 In a free body diagram, forces are correctly labeled and directed along the appropriate axes (horizontal x-axis and vertical y-axis).
  • ⚖️ Newton's second law is introduced as the foundation for analyzing forces, stating that the sum of forces equals mass times acceleration (F = ma).
  • 📊 The scenario involves a block being pushed at a constant speed by a force F, implying kinetic equilibrium (zero acceleration).
  • 🔄 The applied force F_A has both horizontal and vertical components, which are calculated using trigonometric functions (cosine for horizontal and sine for vertical).
  • 🤔 The problem-solving process requires breaking down complex force scenarios into their x and y components for accurate analysis.
  • 👍 Blake's assertion that the net force on the block is zero due to constant velocity is correct, but his understanding of the individual forces involved is flawed.
  • 📌 The correct approach involves analyzing the vertical forces (F_N - F_G + F_pull sine θ) and the horizontal forces (F_friction + F_pull cosine θ) separately.
  • 📈 The solution to the problem involves setting up equations based on the forces acting on the block and solving for the unknowns, such as the normal force and acceleration.
  • 📝 The importance of following a structured approach and checklists is emphasized for solving physics problems accurately and efficiently.
Q & A

  • What are the four basic forces discussed in the AP Physics workbook?

    -The four basic forces discussed are the normal force (F_n), which points away from the surface; the gravitational force (F_g), which points downwards towards the Earth's core; the force of friction (F_f), which points opposite to the direction of forward motion; and the applied force (F_a), which is the force exerted on the object.

  • How is a Freebody diagram labeled for the block in the given scenario?

    -In the Freebody diagram, the force pointing downwards is labeled as F_g (gravity) with a length of 5 units, and the force pointing upwards is also labeled with a length of 5 units. The force to the right, which is the applied force, is labeled as F_a, and the force of friction, which opposes the motion, is labeled as F_f.

  • What does Newton's second law state?

    -Newton's second law states that the sum of all the forces exerted on an object is equal to the object's mass times its acceleration (F = ma).

  • What is the condition for kinetic equilibrium?

    -The condition for kinetic equilibrium is when there is no acceleration (a = 0), which means the object is moving at a constant velocity.

  • How are forces on the vertical (Y-axis) and horizontal (X-axis) analyzed?

    -On the vertical axis (Y-axis), forces such as the normal force (F_n) upwards and gravitational force (F_g) downwards are considered. On the horizontal axis (X-axis), the applied force's horizontal component (F_a cos θ) and the frictional force (F_f) are considered.

  • What happens when the block is in kinetic equilibrium?

    -When the block is in kinetic equilibrium, the net force acting on it is zero. This means the sum of all forces in both the vertical and horizontal directions equals zero.

  • How is the applied force with an angle (θ) broken down into components?

    -The applied force with an angle (θ) is broken down into a horizontal component (F_a cos θ) and a vertical component (F_a sin θ).

  • What are the forces acting on the Y-axis when a pull force is applied at an angle?

    -On the Y-axis, the forces acting are the normal force (F_n) upwards, the gravitational force (F_g) downwards, and the vertical component of the applied force (F_a sin θ).

  • What are the forces acting on the X-axis when a pull force is applied at an angle?

    -On the X-axis, the forces acting are the horizontal component of the applied force (F_a cos θ) and the force of friction (F_f) opposing the motion.

  • What is the total force equation for the system when a pull force is applied at an angle?

    -The total force equation for the system is FN - F_g + F_pull sin θ - F_friction + F_pull cos θ = 0, where FN is the normal force, F_g is the gravitational force, F_pull is the applied force, F_friction is the force of friction, and θ is the angle of the applied force.

  • What was Blake's correct statement about the scenario?

    -Blake's correct statement was that the net force exerted on the block must be zero because the velocity of the block is constant, which is referred to as kinetic equilibrium.

  • What was incorrect about Blake's statements regarding the forces?

    -Blake's statements about the forces were incorrect because he did not properly consider the components of the applied force and the fact that there are both horizontal and vertical forces acting on the block.

Outlines
00:00
📚 Introduction to Dynamics and Basic Forces

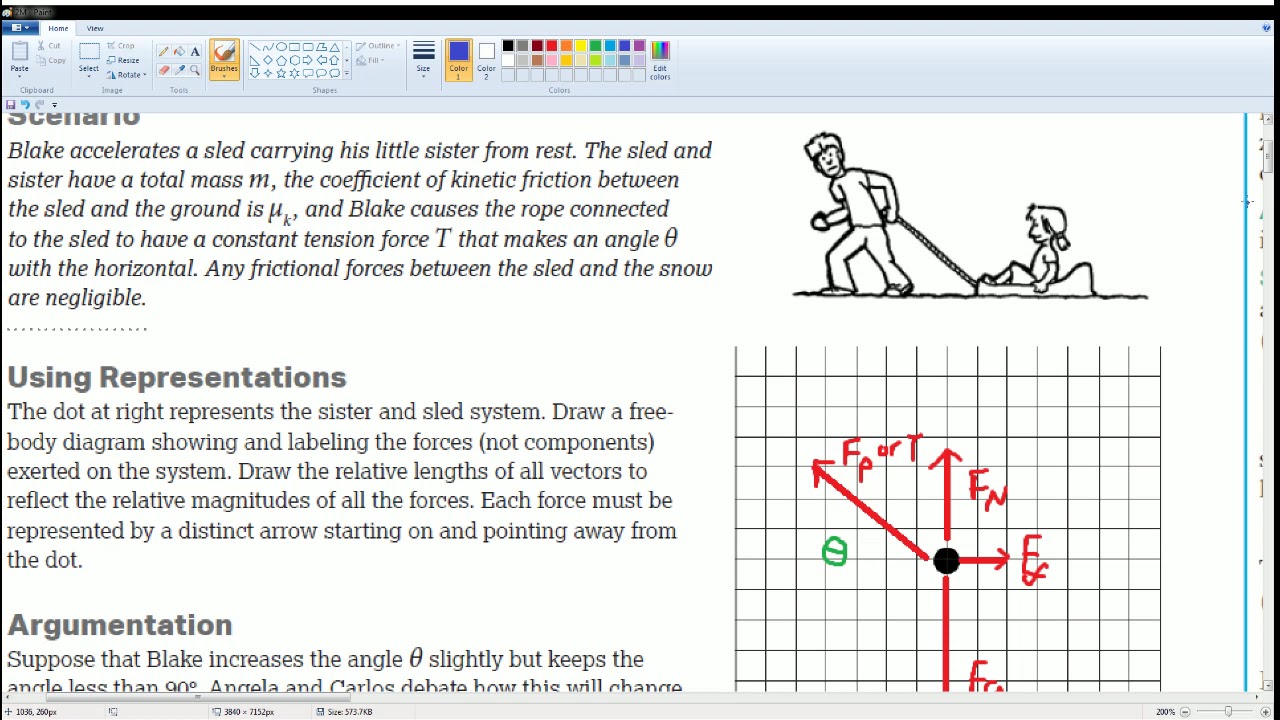
This paragraph introduces the topic of Dynamics from the AP Physics workbook, focusing on Unit 2. It sets the scenario where Carlos pushes a block of mass M across a horizontal surface at a constant speed, applying force F. The paragraph outlines the four basic forces used in the class: the force normal (Sf or N), the force of gravity (Fg or G), the force of friction (Ff or F with a subscript f), and the applied force (FA). It emphasizes understanding the direction of these forces and their relation to the x (horizontal) and y (vertical) axes. The paragraph also explains how to draw a Freebody diagram, labeling all forces and their directions correctly. It concludes with solving Part A of the problem, using Newton's second law to establish that in kinetic equilibrium (constant speed and zero acceleration), the sum of forces equals the mass times acceleration, which is zero in this case, leading to the conclusion that the normal force equals the force of gravity.

05:02
🔍 Analyzing Deviations and Breaking Down Forces

In this paragraph, the focus is on analyzing the forces acting on the block in the given scenario, particularly when an applied force has an angle associated with it (θ). The paragraph explains how to break down the pull force into its x (horizontal) and y (vertical) components using cosine and sine functions. It addresses the common misconceptions made by Blake, who incorrectly assumes the forces but correctly identifies the net force as zero due to constant velocity (kinetic equilibrium). The detailed explanation includes how to calculate the forces in both the vertical and horizontal directions, leading to the correct equations for the total forces in the system. The paragraph concludes with a comprehensive solution for Unit 2, Point C, emphasizing the importance of following checklists and understanding the components of forces acting on an object.

Mindmap
Keywords
💡Forces
In the context of the video, forces are physical interactions that cause an object to change its state of motion. The main theme revolves around understanding how different forces act on an object, such as the block in the example. Forces mentioned include the applied force (F), normal force (FN), gravitational force (FG), and frictional force (Ff). These forces are crucial in analyzing the dynamics of the block, especially when it is moving at a constant speed, indicating a state of equilibrium where the net force acting on the object is zero.
💡Freebody Diagram
A Freebody diagram is a visual representation that shows all the forces acting on an object. It is a fundamental tool in physics for analyzing problems involving forces and motion. In the video, the instructor asks the viewer to draw a Freebody diagram for the block, labeling all the forces correctly and ensuring the lengths represent the magnitudes of the forces. This diagram helps in understanding the dynamics of the system and applying Newton's laws to solve for unknown quantities.
💡Newton's Second Law
Newton's Second Law of Motion states that the net force acting on an object is equal to the mass of the object multiplied by its acceleration (F = ma). This law is central to the video's content as it forms the basis for analyzing the forces acting on the block and determining the conditions for constant velocity or equilibrium. The law helps in understanding how forces affect the motion of objects and is used to solve for unknown forces in the given scenario.
💡Acceleration
Acceleration is the rate of change of velocity of an object with respect to time. It is a key concept in dynamics and is directly related to the forces acting on an object according to Newton's Second Law. In the video, the block is moving at a constant speed, which means its acceleration is zero. This state of zero acceleration indicates that the forces are balanced, and the object is in kinetic equilibrium.
💡Kinetic Equilibrium
Kinetic equilibrium refers to the state when an object is either at rest or moving at a constant velocity, meaning there is no net force acting on the object and no acceleration is occurring. In the video, the block's constant velocity indicates that it is in kinetic equilibrium, which is a key condition for analyzing the forces in the system and applying the concepts of dynamics.
💡Normal Force
The normal force is the force exerted by a surface in a direction perpendicular to the surface, opposite to the weight of an object resting on it. In the video, the normal force (FN) acts upward against the gravitational force (FG) acting on the block. When the block is in kinetic equilibrium, the normal force is equal to the gravitational force, as there is no vertical acceleration.
💡Gravitational Force
Gravitational force, often denoted as FG or mg (where m is the mass of the object and g is the acceleration due to gravity), is the attractive force that a body experiences due to the Earth's gravity. It acts vertically downward and is one of the fundamental forces considered in the analysis of an object's motion. In the video, the gravitational force is one of the key forces that must be balanced for the block to move at a constant speed.
💡Frictional Force
Frictional force is the force that opposes the relative motion or tendency of such motion of two surfaces in contact. It acts parallel to the surfaces in contact and opposite to the direction of motion or the applied force. In the video, the frictional force (Ff) is the force that opposes the applied force (F) and is crucial in maintaining the constant velocity of the block, indicating that the net force is zero.
💡Applied Force
The applied force is the external force that initiates or changes the motion of an object. In the video, the applied force (F) is the force exerted by Carlos to move the block across the surface. This force is a key component in the analysis of the block's motion and is balanced by the frictional force when the block moves at a constant speed.
💡Vector Components
Vector components refer to the individual components of a vector along different axes. In physics, vectors like force can be broken down into their components along the x-axis and y-axis to analyze their effects separately. In the video, when an applied force (F) has an angle (θ) associated with it, it is decomposed into horizontal (cosine θ) and vertical (sine θ) components to understand its impact on the motion of the block.
💡Angles and Forces
In the context of the video, angles and forces are related when an applied force has a direction that is not aligned with the axes. The angle (θ) associated with the applied force affects how the force is resolved into its x and y components. This decomposition is essential for analyzing the dynamics of the system, especially when dealing with non-horizontal or non-vertical forces.
Highlights

The AP Physics workbook introduces Unit 2 Dynamics, focusing on the concept of forces.

Carlos pushes a block of mass M across a horizontal surface at a constant speed, applying a force F to the right.

Four basic forces are discussed in the class: normal force, gravitational force, friction, and applied force.

A Freebody diagram is drawn to visualize and label all forces acting on the block.

The force of gravity is denoted as Fg and is directed downwards with a length of five units.

The normal force is equal in magnitude and opposite in direction to the force of gravity, maintaining kinetic equilibrium.

The x-axis and y-axis are defined, with forces acting along these axes being either horizontal or vertical.

In Part B, Newton's second law is applied to analyze the forces in the vertical and horizontal directions.

The block is in kinetic equilibrium as it moves at a constant speed, with zero acceleration.

The normal force (FN) is equal to the gravitational force (mg) when the block is in equilibrium.

Part C discusses a scenario where the block's velocity is constant, implying a net force of zero.

The force applied (F) has an angle θ associated with it, which is broken down into x and y components.

The x-component of the applied force is represented by the cosine of θ, and the y-component by the sine of θ.

In the vertical direction, there are three forces acting: the normal force, gravitational force, and the y-component of the applied force.

In the horizontal direction, there are two forces: the frictional force opposite to motion and the x-component of the applied force.

The total force in the system is the sum of forces in the vertical (Fy) and horizontal (Fx) directions.

The correct equation for the total force in the system is FN - mg + Fpull * sin(θ) - friction + Fpull * cos(θ).

Blake's claim that the net force must be zero due to constant velocity is correct, but his understanding of the individual forces is incorrect.

The correct statements involve the decomposition of the applied force into its components and the balance of forces in both vertical and horizontal directions.

Transcripts

Browse More Related Video

AP Physics Workbook 2.M Limiting Cases

What is a Force & Types of Forces in Physics? - Gravity, Normal Force, Contact Forces - [1-5-1]

Introduction to Inclined Planes

AP® Physics 1: Forces and Newton's Laws (Unit 2)

AP Physics Workbook 3.E Maximum speed over the top

AP Physics Workbook 2.F Direction of Friction

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
PhysicsConceptsForceAnalysisWorkbookSolutionsAPPhysicsMechanicsConstantVelocityKineticEquilibriumFreebodyDiagramMathematicalMethodsEducationalContent