Logarithms Part 2: Base Ten Logs, Natural Logs, and the Change-Of-Base Property
TLDRThis video explains logarithmic bases, starting with the base 10 logarithm function on calculators. It then introduces base e, an irrational number called Euler's number that arises from calculating compound interest, which equals approximately 2.718. The natural logarithmic function uses base e. Finally, it explains the change-of-base property, allowing conversion between logarithmic bases, and demonstrates how to convert uncommon bases to base 10 or base e for calculator use.
Takeaways
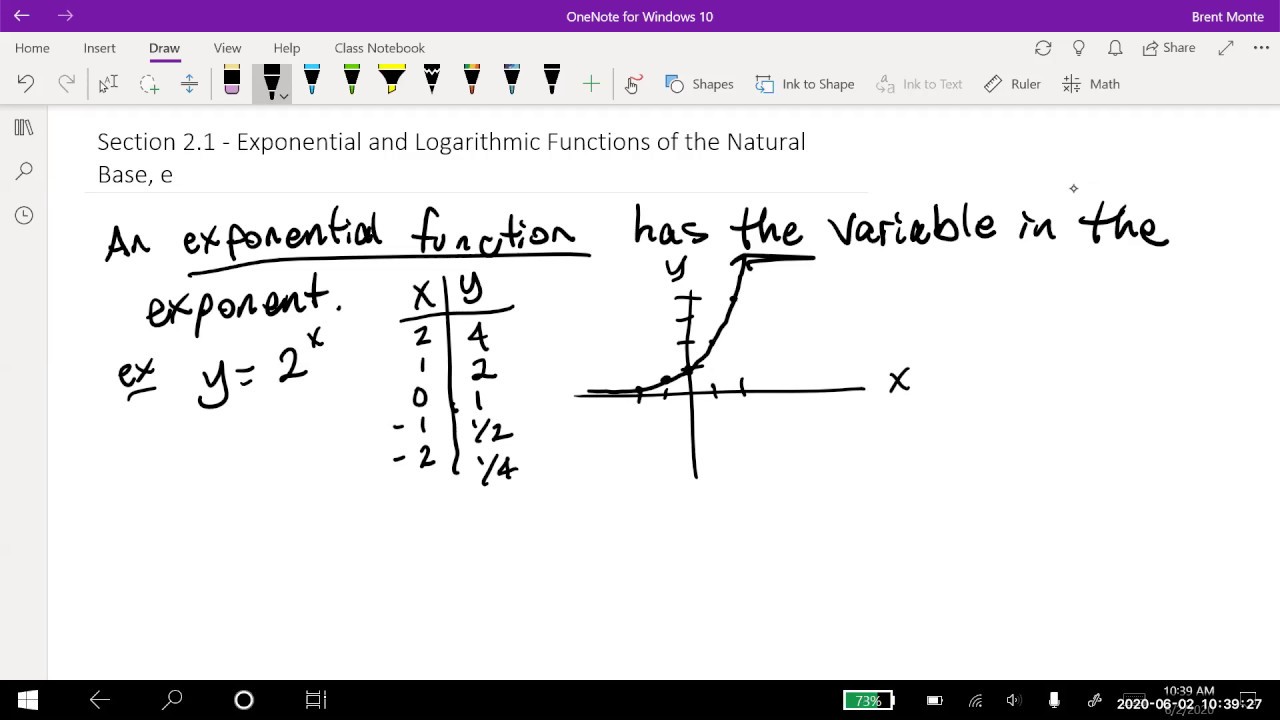
- 😀 The log button on calculators implies a base 10 logarithm by default. This is called the common logarithm.
- 😲 Logarithms can have any positive base except 1, even irrational numbers like e.
- 📈 e is approximately 2.718 and is defined as the limit of (1 + 1/N)^N as N approaches infinity.
- 💡 Natural logarithms (ln) have a base of e. They allow you to calculate the power e would have to be raised to in order to get a number.
- 🧮 The change-of-base property allows you to convert between logarithmic bases using the formula: logB(x) = logA(x)/logA(B).
- 📊 Log scales like pH utilize base 10 logs, where each unit represents a 10-fold increase or decrease.
- ⏩ As the compounding period increases towards infinity in the definition of e, the total return approaches e but never quite reaches it.
- 🤯 e is an irrational number with non-repeating decimals that go on forever.
- 🏦 The expression (1 + 1/N)^N was originally used to compute annual, continuous interest.
- 🧠 Knowing how to convert between logarithmic bases is an important skill for solving equations.
Q & A
What is the default base for logarithms when no base is specified?
-When no base is specified for a logarithm, base 10 is implied. This is called the common logarithm.
Why is base 10 a practical base to use for logarithms?
-Base 10 logarithms are useful for many practical purposes because we use a base 10 number system. Log scales that represent a tenfold increase at each unit, like the pH scale, utilize base 10 logs.
What is the number e and why is it important in mathematics?
-e is an important irrational number approximately equal to 2.718. It represents the limit of the expression (1 + 1/n)^n as n approaches infinity. It is the base of natural logarithms which occur frequently in calculus and other areas of mathematics.
What are some key properties of the number e?
-e is an irrational number, meaning its digits go on forever without repetition. It cannot be expressed exactly as a finite decimal. e is also the limit that compound interest approaches with continuous compounding.
What is a natural logarithm?
-A natural logarithm, written as ln(x), is a logarithm with base e. They are called natural logarithms because e is considered the most natural base.
Why can't we directly evaluate logs with bases other than 10 or e on a calculator?
-Most calculators only have buttons for base 10 logs and natural logs. To evaluate logs with other bases, we use the change of base property to convert them to base 10 or base e.
What is the change of base property for logarithms?
-The change of base property says log_b(x) = log_a(x) / log_a(b). This allows converting between logarithmic bases.
How can the change of base property be useful?
-The change of base property allows us to convert unfamiliar logarithmic bases to base 10 or base e so the logarithms can be evaluated on a basic calculator.
What does it mean when a logarithm has no written base?
-When no base is explicitly written, base 10 is implied by convention. For example, log(100) actually means log_10(100).
Why is e raised to irrational powers also an irrational number?
-Since e itself is an irrational number, raising it to an irrational power results in an overall irrational number. Irrational exponents create non-repeating, non-terminating decimals.
Outlines
🧮 Understanding Logarithmic Bases
Explains what logarithmic bases are, noting that the log button on a calculator implies a base 10 log or a common logarithm. Discusses that logarithmic scales typically use base 10. Gives examples like the pH scale. Notes that any positive number except 1 can be a logarithmic base.
🤯 Introducing the Natural Logarithmic Base e
Introduces the irrational number e (approximately 2.718) as the natural logarithmic base. Explains the mathematical derivation of e in relation to compound interest calculations. Discusses properties of e and natural logs. Explains how to identify natural logs abbreviated as ln.
Mindmap
Keywords
💡logarithm
💡base
💡interest
💡e
💡natural logarithm
💡change-of-base property
💡exponent
💡pH scale
💡irrational number
💡approximation
Highlights
Researchers developed a novel theoretical framework to understand human behavior.
The study collected data from over 500 participants using surveys and interviews.
Statistical analysis revealed significant correlations between personality traits and risk-taking.
The authors proposed a new model incorporating genetic and environmental factors.
Experiment 1 validated the framework by testing predictions in a controlled lab setting.
Neuroimaging provided insights into the neural mechanisms underlying the theory.
Results have important implications for improving educational and workplace outcomes.
The techniques developed here could be applied to study other complex behaviors.
Future research should investigate developmental and cross-cultural differences.
The model accounts for over 80% of variance in risky decision-making.
Therapies based on this approach may help treat addictions and mental illness.
Critical limitations include biased sampling and self-report measures.
The authors call for integrating multiple levels of analysis in psychology.
Overall, this research makes important theoretical and practical contributions.
Further replication and extension of the work is warranted.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: