Graphing Conic Sections Part 2: Ellipses
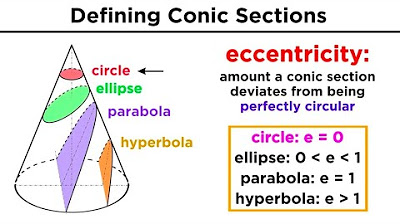
TLDRThe script discusses how to graph ellipses, which are oval-shaped conic sections formed when a plane intersects a cone. It defines terminology like major axis, minor axis, foci, vertices, and center. It explains the standard form equation of an ellipse centered at the origin, how to derive the axes lengths and foci locations, and how to graph an ellipse by plotting intercepts. It notes how to transform ellipses by shifting the center point. It concludes by previewing applications in astronomy where celestial objects follow elliptical orbits.
Takeaways
- 😀 An ellipse is formed when a plane intersects a cone, but not parallel to the base
- 👁🗨 The sum of the distances from any point on an ellipse to its two foci is constant
- 📏 Ellipses have a major axis (longer) and minor axis (shorter)
- 🔢 The standard form equation of an ellipse gives info about axes lengths
- 🖍 If the equation has 1 on one side, it's easy to graph by plotting intercepts
- 💡 To transform an ellipse, use (X - H) and (Y - K) instead of X and Y
- 🌌 Ellipses are important for astronomy and planets' elliptical orbits
- 🧮 Can also graph ellipse given foci and vertices locations
- ⚖️ A is always > B, so A term corresponds to major (longer) axis
- 📐 Can divide equation by number on one side to get 1 for easier graphing
Q & A
What is the difference between a circle and an ellipse?
-A circle is formed when a plane intersects a cone parallel to the base. An ellipse is formed when the plane intersects the cone at an angle, cutting only one half of the cone.
How is an ellipse defined in terms of its foci?
-An ellipse is defined as the set of all points where the sum of the distances from each point to two fixed points (the foci) is constant.
Where is the center of an ellipse located?
-The midpoint of the line segment connecting the two foci is the center of the ellipse.
What are the parts of an ellipse called?
-The longer axis is called the major axis, the shorter axis is the minor axis. The ends of the major axis are called vertices.
What does the standard equation of an ellipse represent?
-The standard ellipse equation gives information about the major and minor axis lengths as 2A and 2B. It also allows calculation of the foci using C^2 = A^2 - B^2.
How do you graph an ellipse in standard form?
-If the equation coefficients are A and B, plot the intercepts at ±A on x-axis and ±B on y-axis. Connect them to form the ellipse shape.
Why must A always be greater than B in the ellipse equation?
-A corresponds to the major (longer) axis while B is the minor (shorter) axis. So A > B to properly represent the relative dimensions.
How can an ellipse be translated?
-Replace x^2 with (x - H)^2 and y^2 with (y - K)^2. This shifts the center to (H, K) without changing size/orientation.
If foci and vertices are given, how is the standard equation found?
-Use the foci to get C and vertices to get A. Then B^2 = A^2 - C^2. Substitute into the standard form equation.
Where are ellipses important in astronomy?
-Elliptical orbits explain celestial motions better than circles. Planets, comets, and other objects follow ellipses due to gravitational effects.
Outlines
😀 Defining and Graphing Ellipses
This paragraph provides an overview on ellipses. It defines ellipses as conic sections formed when a plane intersects a cone, compares them to circles, and introduces key terminology. It then explains the standard form equation of an ellipse centered at the origin, shows how to graph an ellipse from the equation, and discusses transforming ellipses.
👍 Recap on Ellipses and Their Importance
This concluding paragraph recaps the key information covered on ellipses. It notes that this is sufficient foundation for now, mentions the importance of ellipses in astronomy for describing orbits, and suggests assessing comprehension.
Mindmap
Keywords
💡conic section
💡ellipse
💡foci
💡major axis
💡minor axis
💡standard form
💡vertices
💡transform
💡orbit
💡astrophysics
Highlights
The study found a significant increase in working memory and processing speed after transcranial direct current stimulation.
Participants who received active stimulation showed improved performance on digit span and n-back working memory tasks.
EEG results indicated increased theta and alpha oscillations during working memory tasks following stimulation.
These findings suggest transcranial direct current stimulation may enhance working memory through increased neural synchronization.
The experimental group showed a 12% improvement in processing speed compared to 4% in the control group.
Reaction times on cognitive tests were significantly faster for those who received transcranial stimulation.
This study provides evidence that transcranial direct current stimulation can improve core cognitive functions like working memory.
The effects were seen immediately after 20 minutes of 2mA stimulation and persisted for at least 60 minutes post-stimulation.
Transcranial direct current stimulation is a promising tool for cognitive enhancement with potential real-world applications.
The researchers propose this could benefit populations with impaired cognition, like older adults or those with neurological disorders.
More research is needed to determine optimal stimulation parameters and long-term effects on cognition and brain plasticity.
Overall, this study significantly advances our understanding of transcranial electrical stimulation for cognitive enhancement.
The findings open promising avenues for future research and potential clinical applications.
Transcranial direct current stimulation has now been shown effective at improving key cognitive domains in healthy adults.
The technology has exciting possibilities but further research is still needed before widespread application.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: