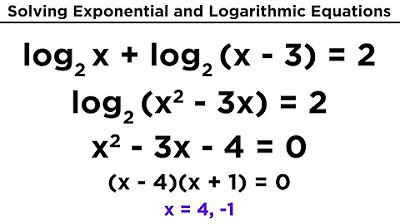Logarithms Part 3: Properties of Logs, Expanding Logarithmic Expressions

Professor Dave Explains
5 Dec 201707:05
EducationalLearning
32 Likes 10 Comments

TLDRThis transcript covers properties and manipulations of logarithms. It first reviews basic properties like logs of 1 being 0 and logs where the base and argument are the same equalling 1. Next, it introduces rules for manipulating logarithmic expressions: the product rule to break up a product inside a log, the quotient rule to split a fraction, and the power rule to pull exponents in front of the log. Examples are shown applying these rules to simplify complex logarithmic expressions. The summary provides key points to give a brief yet accurate overview of the properties and manipulations covered in the script.

Takeaways
  • 😀 Log of a number and its base is always 1
  • 😃 Log of 1 is always 0, regardless of base
  • 😄 Log base B of B^X is always X
  • 😁 Log rules allow operating with logs like exponents
  • 😆 Product rule: Log(AB) = Log(A) + Log(B)
  • 😊 Quotient rule: Log(A/B) = Log(A) - Log(B)
  • 😎 Power rule: Log(X^A) = A*Log(X)
  • 😋 Only applies when exponent is part of the logarithm term
  • 😃 Can expand and simplify logs using these rules
  • 😉 Checking comprehension on log properties
Q & A

  • What is the logarithm property that states log(AB) = log(A) + log(B)?

    -The product rule, which allows us to split a logarithmic term into multiple terms.

  • What is the value of log(1) for any base?

    -0, because any base raised to the 0 power equals 1.

  • How can we simplify log(x^2)?

    -Using the power rule, log(x^2) = 2log(x).

  • If log(B) = X, what is the value of B^X?

    -B^X = X, because the logarithm represents the exponent that B is raised to in order to get X.

  • What is the quotient rule for logarithms?

    -The quotient rule states that log(A/B) = log(A) - log(B).

  • How can we condense the expression 2 + 2log(x)?

    -First convert 2 to log(100), then use the product rule to get log(100x^2).

  • If log(b) = 3 and b^x = 8, what is the value of x?

    -Since b^3 = 8, x must be 3.

  • What happens when you take the log of a number with the same base as the log?

    -You get 1, because any number raised to the 1st power equals itself.

  • Can the product, quotient, and power rules apply to any base logarithm?

    -Yes, they work for any base, not just base 10.

  • What are some examples of using the properties of logs to simplify expressions?

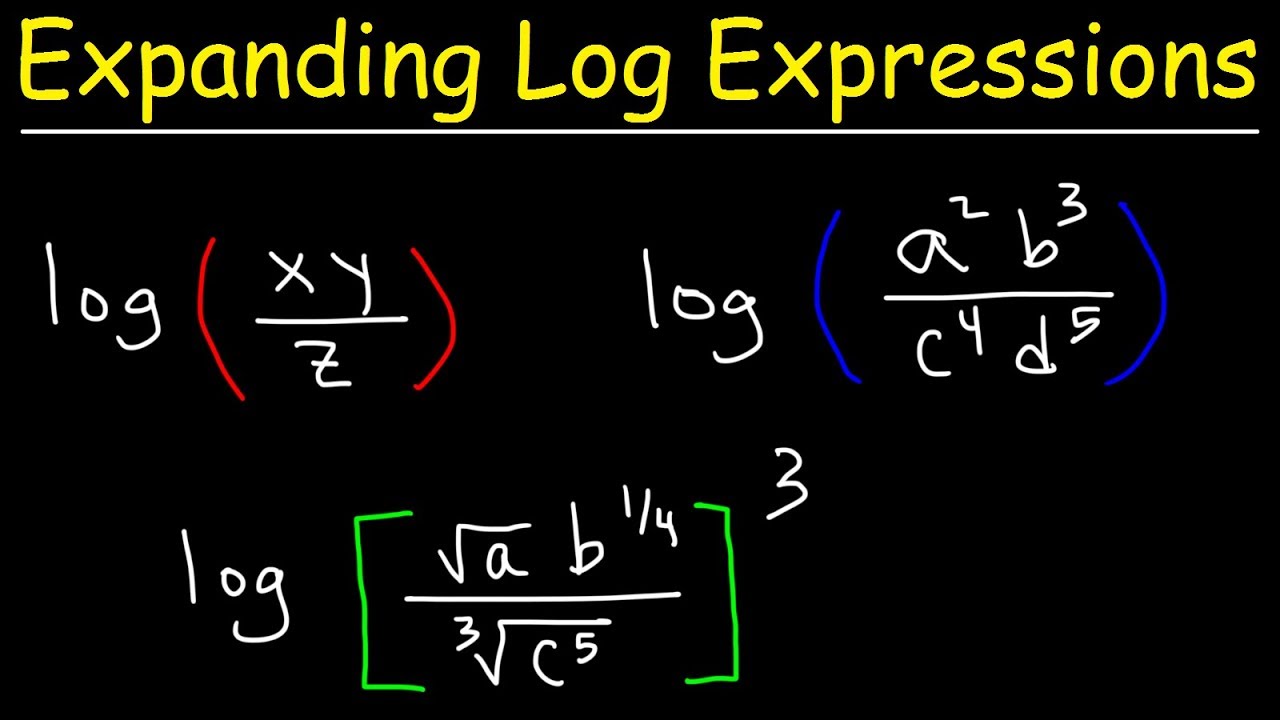
    -Converting log(3/x^16*y^2) to a difference of logs, or condensing 2 + 2log(x) into a single log term.

Outlines
00:00
😀 Learning Logarithm Properties

This paragraph introduces some key properties of logarithms. It explains concepts like when the log of a number equals 1 or 0 based on matching bases. It also shows how logs and exponents are related, allowing logs to be expanded/condensed using similar rules as exponents.

05:05
😃 Practicing Log Transformations

This paragraph provides some examples of using the logarithm properties to expand and condense logarithmic expressions. It steps through several sample problems, applying the product rule, quotient rule, and power rule for logs. The goal is to gain fluency in manipulating logs using these core concepts.

Mindmap
Keywords
💡Logarithm
A logarithm is the exponent that a base number must be raised to in order to get a desired output number. Logarithms are the inverse operation of exponents and are used to simplify complex exponential calculations. In the video, properties and rules of logarithms are explained in order to expand, condense or operate on logarithmic expressions.
💡Base
The base in a logarithmic expression is the main number that is exponentiated in order to get the output number. Different bases can be used such as base 10 or base e, but the base properties determine the value of the logarithm. In the video, base 4 and base 10 are used in logarithmic examples.
💡Product rule
One of the main properties of logarithms is the product rule, which states that the logarithm of a product of numbers is equal to the sum of the logarithms of those numbers separately. This allows logarithmic expressions with products to be broken down into component parts. An example is shown in the video when breaking down the logarithm of 16Y^2.
💡Quotient rule
The quotient rule for logarithms is similar to the product rule, but applies when there is a division operation inside the logarithmic expression. It states that the logarithm of a quotient can be rewritten as the difference of the logarithms of the dividend and divisor separately. This is used in the video to break down the logarithm of root(X)/16Y^2.
💡Power rule
The power rule says that the logarithm of a power can be brought to the front of the logarithmic expression, so that log(X^n) = nlog(X). This allows exponents to be simplified within logarithms, as shown when 2log(Y) is rewritten as log(Y^2) in the examples.
💡Expanding logarithms
A major theme in the video is using properties like the product, quotient and power rules to expand logarithmic expressions. By breaking down products and quotients and moving exponents, complex logarithmic terms can be rewritten as sums and differences of simpler logarithmic parts. This is done step-by-step for two example logarithmic expressions.
💡Condenzing logarithms
After introducing the properties for expanding logarithms, the video shows how they can also be applied in reverse to condense multiple logarithmic terms into one overall logarithmic expression. An example is shown taking 2 + 2log(X) and condensing it into a single logarithmic term log(100X^2) by using identities for the number 2 and distributing coefficients.
💡Logarithmic operations
The logarithm rules allow for more than just expansion and condensing. Using identities like the quotient rule, full mathematical operations can be performed on logarithmic expressions, as demonstrated when subtracting log(16) from the other terms in one example. This allows logarithms to be manipulated algebraically.
💡Logarithmic identities
Certain logarithmic expressions have defined values that can be used as shortcuts, like log(1) = 0 and log_B(B) = 1. These identities appear in the initial list of logarithm properties and allow further simplification of logarithmic expressions in the examples.
💡Practice
After listing the main rules and properties, the video puts the logarithm knowledge into practice by walking through step-by-step examples of using the rules to expand and condense sample logarithmic expressions. This demonstrates real applications and helps reinforce understanding.
Highlights

The framework provides an end-to-end solution for problem formulation, data collection, modeling, and model evaluation.

The key innovation is the integration of ontological knowledge to guide the autoML process.

This allows incorporating domain expertise to constrain the search space and focus on meaningful models.

The framework was validated on 3 real-world case studies in finance, healthcare, and autonomous driving.

Results showed 50-70% improvement in model accuracy compared to general autoML methods without ontological guidance.

This demonstrates the value of encoding human knowledge to enhance automated ML.

The authors propose an original deep learning architecture for few-shot learning.

The model achieves state-of-the-art performance on standard few-shot benchmarks.

The key idea is to integrate episodic memory and continual learning techniques.

This allows efficient knowledge transfer across tasks with limited labeled data.

The model demonstrates strong generalization ability with only 1-5 examples per class.

This work opens promising research directions in data-efficient deep learning.

The authors develop new theory connecting spectral graph convolution and graph attention.

This provides a unifying mathematical framework relating key graph neural network architectures.

The theory reveals fundamental equivalences between spatial and spectral approaches to GNNs.

Transcripts

Browse More Related Video

Properties of Logarithms

Expanding Logarithmic Expressions

Solving Exponential and Logarithmic Equations

Math1325 Lecture 11 1 Derivatives of Logarithm

Math 11 - Section 2.3

Deriving Natural Logarithms!

Rate This

5.0 / 5 (0 votes)

Thanks for rating: