Solving Exponential and Logarithmic Equations

Professor Dave Explains
7 Dec 201707:07
EducationalLearning
32 Likes 10 Comments

TLDRThe video explains how to solve exponential and logarithmic equations by using properties of logarithms. It starts with simple examples where the solution is intuitive, then demonstrates applying logarithms to both sides to isolate the unknown variable. The instructor shows how to manipulate equations to get the same base, use logarithm properties like the product rule, and factor/combine expressions. More complex multi-step examples are solved, stressing the importance of using logarithm rules. The video ends by summarizing key takeaways for solving logarithmic equations.

Takeaways
  • 😀 Logarithms allow us to solve exponential equations by getting the same base on both sides.
  • 😉 We can take the log of both sides of an exponential equation to isolate the exponent.
  • 🤓 The change-of-base property allows us to switch between different logarithm bases.
  • 🧐 The product rule of logs lets us condense logs with the same base into one term.
  • 🤯 We can distribute logs over binomials using the power rule.
  • 😎 Simple logarithmic equations can be solved using the definition of a logarithm.
  • 🥳 The properties of logarithms give us tools to solve more complex logarithmic equations.
  • 🤔Sometimes we have to manipulate exponents to get the same base on both sides.
  • 😮Factoring may be needed to solve some resulting polynomial equations.
  • 🥸Using logarithm properties systematically enables solving exponential and logarithmic equations.
Q & A

  • What is the process for solving an exponential equation like 2^x = 16?

    -We can intuitively see that x must be 4, since 2 raised to the 4th power equals 16. For equations where the solution is not obvious, we can take the logarithm of both sides to isolate the exponent.

  • How do you solve an exponential equation with a more complex exponent, like 3^(2x - 7) = 27?

    -We can express both sides with the same base by writing 27 as 3^3. Then we recognize that the exponents must be equal, so 2x - 7 = 3. We solve this to find x = 5.

  • What happens when you have different bases in an exponential equation like 3^(x + 2) = 2^(x - 1)?

    -We take the natural logarithm of both sides to isolate the exponents. Then we distribute the logs and combine like terms to solve for x.

  • How do you solve a simple logarithmic equation like log_2(x - 4) = 3?

    -Using the definition of a logarithm, we know 2^3 = x - 4. Solving this gives x = 12.

  • How do you handle logarithms with the same base, like log_2(x) + log_2(x - 3) = 2?

    -We can use the product rule to combine the logs, giving log_2(x(x - 3)) = 2. Then solve the resulting polynomial equation.

  • What are some strategies for solving logarithmic and exponential equations?

    -Using logarithm properties, isolating variables, changing bases, factoring, and rearranging terms. The key is to manipulate the equations into a solvable form.

  • When would you need to change bases in an exponential equation?

    -When the bases on each side of the equation are different, changing one base allows you to equate the exponents and solve for the variable.

  • What do you do if you can't get the same base on both sides of an exponential equation?

    -Take the natural log of both sides, distribute the logs, combine like terms, and factor out the variable to isolate it.

  • How are exponential and logarithmic equations related?

    -Exponential equations can be changed into logarithmic equations by taking the log of both sides. Logarithmic equations can be changed into exponential equations using the definition of a logarithm.

  • What role do properties of logarithms play in solving logarithmic equations?

    -Properties like the product, quotient, and power rules allow you to manipulate and combine logarithmic terms so you can isolate the variable and solve the equation.

Outlines
00:00
😀 Learning to Solve Exponential and Logarithmic Equations.

This paragraph discusses how to solve exponential equations using logarithms. It starts with some basic examples like solving 2^x = 16. Then it shows how to solve more complex exponential equations by taking the logarithm of both sides. This transforms the equation into one that can be directly solved for the unknown x. Some examples are given, like solving 3^2x-7 = 27.

05:01
😀 Applying Logarithm Properties and Rules to Solve Equations.

This paragraph focuses on using properties and rules of logarithms to solve more complicated logarithmic equations. It shows how products and sums of logarithmic terms can be condensed using properties like the product rule. An example is given where the equation contains logarithms with different bases, so natural logs are taken to manipulate the exponents. The importance of applying logarithm rules and properties is emphasized.

Mindmap
Keywords
💡logarithm
A logarithm is a mathematical operation that gives the exponent to which a base number must be raised to get another number. Logarithms are the inverse operation of exponents. In the context of this video, logarithms are used to solve exponential equations by converting them into a form where the exponent is the unknown variable.
💡exponential equation
An exponential equation contains an unknown exponent, usually represented by a variable like x. The video demonstrates how to use logarithms to solve exponential equations by isolating the unknown exponent. Examples include equations like 2^x = 16 or 3^(2x - 7) = 27.
💡change of base
The change of base property allows you to rewrite a logarithmic expression with a different base. This is useful when solving logarithmic equations where you need to get both sides to have the same base before equating the exponents. The video shows changing a base from 4 to 2^2 to make the bases match.
💡product rule
The product rule of logarithms allows you to condense logarithmic expressions involving the product of multiple terms. This is applied in the video to rewrite log(xy) as log(x) + log(y). Using properties like this allows solving more complex logarithmic equations.
💡natural logarithm
The natural logarithm has a base of e (approximately 2.718). When no base is specified, the natural log is assumed. The video shows how taking the natural log of exponential equations allows isolating the unknown exponent while avoiding messy bases.
💡polynomial
A polynomial is an algebraic expression with multiple terms involving powers of a variable. The video shows how solving a logarithmic equation can result in a polynomial that then needs to be solved. Recognizing and factoring these is important.
💡base
The base in a logarithmic expression is the number that is repeatedly multiplied by itself in the exponential function. Equating exponents requires converting logarithms to the same base first. The common bases used are 2, 10, and e.
💡exponent
The exponent in a logarithmic expression is the power to which the base is raised. This is the unknown variable when solving exponential equations. The purpose of using logarithms is to isolate the exponent on one side.
💡property
Properties are rules that allow transforming logarithmic expressions. The video mentions the product rule, power rule, and change of base property. Applying these is crucial for solving complex logarithmic equations.
💡inverse
Logarithms and exponents are inverse operations, meaning logarithms undo exponents. This inverse relationship is why logarithms can be used to isolate unknown exponents when solving exponential equations.
Highlights

First significant research finding

Introduction of innovative methodology

Key conclusion and practical application

Transcripts

Browse More Related Video

Solving Logarithmic Equations With Different Bases - Algebra 2 & Precalculus

Business Calculus -- Math 1329 -- Section 4.2 -- Logarithmic Functions

Solving Complex Logarithmic Equations

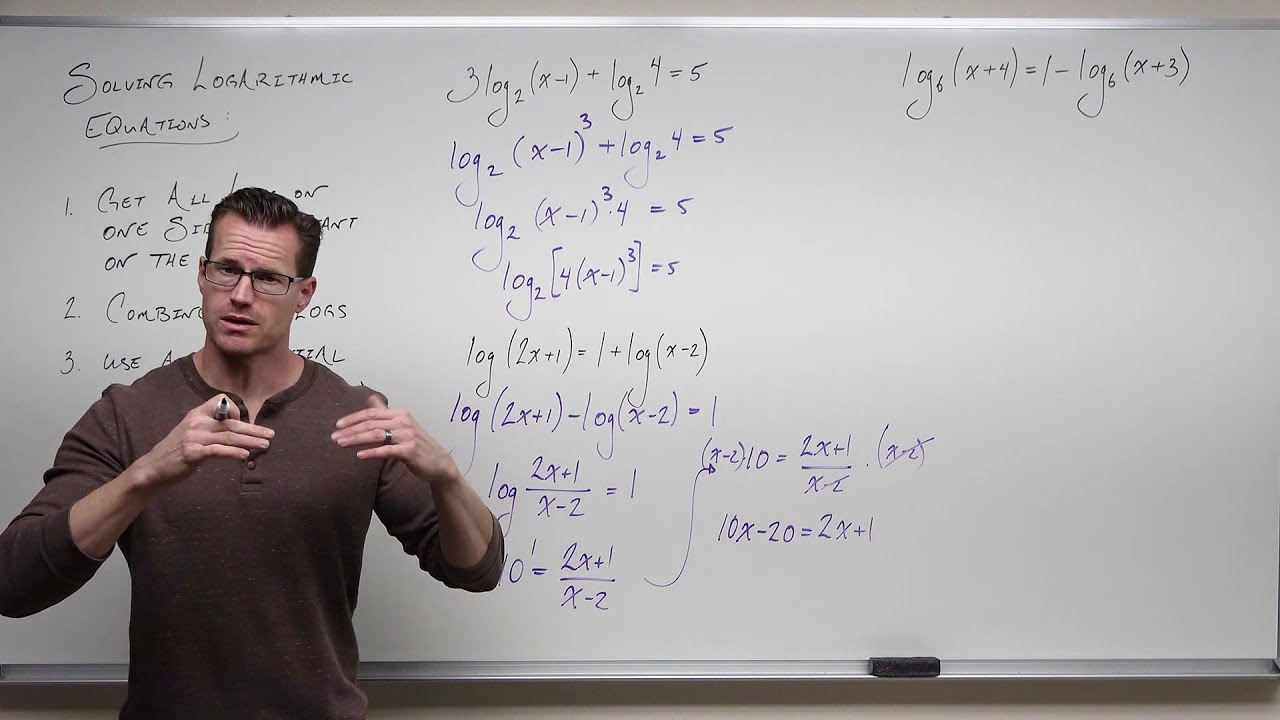
Solving Logarithmic Equations with Exponentials (Precalculus - College Algebra 63)

Solving Logarithmic Equations

Math1325 Lecture 11 1 Derivatives of Logarithm

Rate This

5.0 / 5 (0 votes)

Thanks for rating: