Evaluating and Graphing Exponential Functions

Professor Dave Explains
29 Nov 201705:59
EducationalLearning
32 Likes 10 Comments

TLDRThe script explains exponential functions, where the variable is the exponent. These grow rapidly as the variable increases. The number raised to the exponent is the base. Exponential functions model real-world situations like population growth. They are easy to evaluate and graph by following base rules. Transformations like shifting, reflecting, and stretching can be applied just like with parabolas. The domain is all real numbers and range is all reals greater than zero.

Takeaways
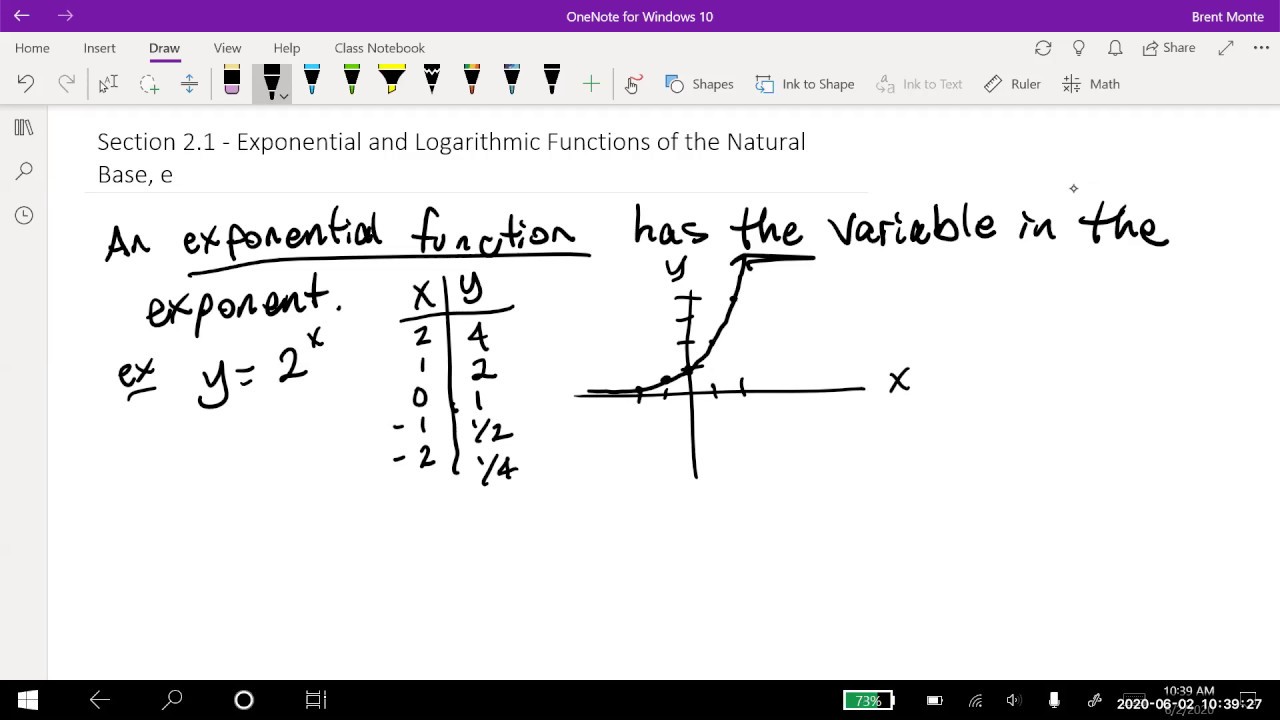
  • 😀 Exponential functions have a variable in the exponent position, like 2^x, and grow very rapidly.
  • 😲 The base must be positive and not equal to 1. Changing the base produces different exponential functions.
  • 😃 Exponential functions can model real-world situations like population growth and disease spread.
  • 🔢 Exponential functions are easy to evaluate on a calculator by substituting the x-value.
  • 📈 If the base is >1 and exponent is positive, the function rises. If the base is <1 and exponent is positive, the function dips.
  • 📉 If the base is >1 and exponent is negative, the function dips. If the base is <1 and exponent is negative, the function rises.
  • 🌐 The domain is all real numbers. The range is all real numbers greater than 0.
  • 🖼️ Transformations like shifts, reflections, and stretches can be applied to graph alterations of the basic exponential function.
  • ❗ The variable term is the exponent. The number being raised is called the base.
  • 🧮 Exponential functions can model things like population growth, bacterial growth, and disease spread where rapid increase occurs.
Q & A

  • What is an exponential function?

    -An exponential function is one where the variable is used as an exponent, such as 2^x. The exponent can grow or shrink very rapidly as the variable changes.

  • What is the base in an exponential function?

    -The base is the number that is raised to the power of the exponent. For example, in 2^x, the base is 2.

  • How can exponential functions model real-world situations?

    -Exponential functions can model situations where there is rapid increase or decrease, like population growth, bacterial cultures, or the spread of diseases.

  • How do you evaluate exponential functions?

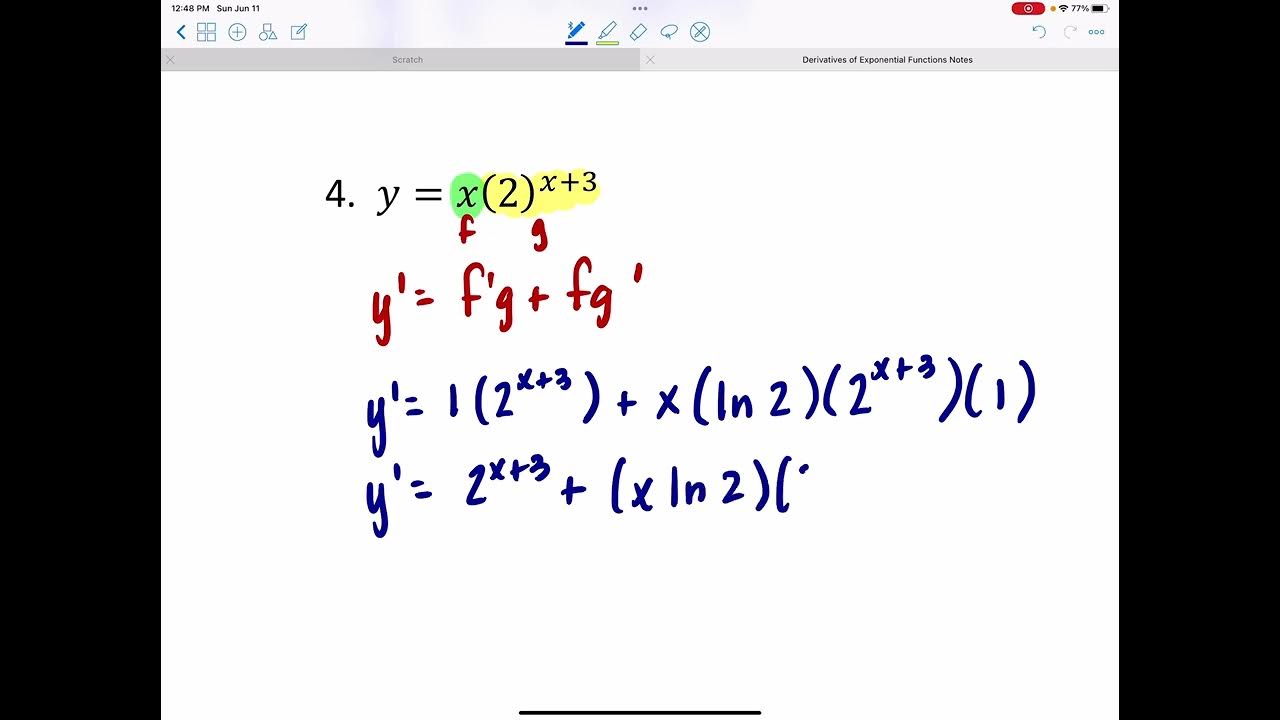
    -To evaluate exponential functions, substitute the given value for the variable and simplify using the rules of exponents. For example, to evaluate 1.5 * 4^x when x=3, cube 4 to get 64, then multiply by 1.5 to get 96.

  • What are the key features of exponential function graphs?

    -Exponential function graphs have horizontal asymptotes on the x-axis. If the base is greater than 1, the graph rises up as x increases. If the base is between 0 and 1, the graph falls as x increases.

  • How can you transform exponential function graphs?

    -You can shift exponential graphs vertically or horizontally, reflect them over the x or y axis, or stretch/compress them vertically or horizontally using the same techniques as for parabolas.

  • What is the domain and range of exponential functions?

    -The domain of exponential functions is all real numbers. The range is all real numbers greater than zero.

  • When does an exponential function increase or decrease?

    -If the base is greater than 1 and the exponent is positive, or the base is between 0 and 1 and the exponent is negative, the function increases. If the base is less than 1 and the exponent is positive, or the base is greater than 1 and the exponent is negative, the function decreases.

  • What happens to an exponential function as the exponent approaches positive infinity?

    -As the exponent approaches positive infinity, exponential functions with bases greater than 1 approach positive infinity. Exponential functions with bases between 0 and 1 approach 0.

  • What happens to an exponential function as the exponent approaches negative infinity?

    -As the exponent approaches negative infinity, exponential functions with bases greater than 1 approach 0. Exponential functions with bases between 0 and 1 approach positive infinity.

Outlines
00:00
😀 Introducing Exponential Functions

This paragraph introduces the concept of exponential functions, explaining that they have a variable in the exponent position rather than the base position. It plots some points to show how the function grows rapidly as the input value increases. The base number that is raised to the exponent can be different to produce different exponential functions. The exponent can also be an expression. Exponential functions can model real-world situations like population growth and disease spread where rapid increase/decrease occurs.

Mindmap
Keywords
💡Exponential function
An exponential function is one where the variable is an exponent, such as 2^x. This results in very rapid growth or decay as the variable increases or decreases. Exponential functions are important for modeling situations with exponential growth or decay, like population growth, bacterial cultures, or the spread of diseases.
💡Base
The base in an exponential function is the number that is raised to the exponent. For example, in 2^x, the base is 2. Changing the base produces different exponential functions with different growth rates.
💡Exponent
The exponent in an exponential function is the variable, such as x in 2^x. As the exponent increases, an exponential function grows rapidly towards positive infinity. As the exponent decreases, the function decays towards zero.
💡Domain
The domain of an exponential function is all real numbers. This means any real number can be input as the exponent.
💡Range
The range of an exponential function is all positive real numbers greater than zero. Exponential functions do not output negative values or zero.
💡Horizontal asymptote
Exponential functions have a horizontal asymptote along the x-axis. This means as the input increases or decreases, the function approaches but never reaches the x-axis.
💡Transformations
We can apply transformations like shifts, reflections, and stretches to exponential functions just as with quadratic functions. This alters the basic exponential shape.
💡Population growth
Population growth often follows an exponential pattern, especially in rapidly reproducing organisms like bacteria. Exponential functions can model this exponential growth in populations.
💡Disease spread
The spread of infectious diseases epidemically often follows an exponential pattern. Exponential functions are used to model the rapid growth in disease transmission.
💡Calculators
Exponential functions are easy to evaluate using calculators, by simply inputting the base and exponent. For example, to evaluate 1.5 * 4^3, we cube 4 to get 64, then multiply by 1.5.
Highlights

First significant research finding

Introduction of innovative methodology

Key conclusion and practical applications

Transcripts

Browse More Related Video

Graphs of Exponential Functions (Precalculus - College Algebra 52)

Exponential Functions!

Derivatives of Exponential Functions

Math 11 - Section 2.1

BusCalc 14 Derivatives of Exponents

Math1325 Lecture 11 2 - Derivatives of Exponential

Rate This

5.0 / 5 (0 votes)

Thanks for rating: