Three-Dimensional Shapes Part 2: Calculating Volume
TLDRThe script explains how to calculate the volumes of various 3D shapes including cubes, rectangular prisms, triangular prisms, cylinders, pyramids, cones, and spheres. It provides the formulas for finding the volumes based on dimensions like side lengths, radii, and heights. The concepts build from simpler shapes like cubes and rectangular prisms to more complex ones like pyramids, cones, and spheres. The script also notes that for irregular shapes with unpredictable curvature, calculus would be required to determine volumes.
Takeaways
- 😀 We learned how to calculate the 3D volume of objects, not just their 2D surface area
- 😯 Volume is found by multiplying the area of the base by the height/depth
- 📏 This works for any prism shape - cubes, rectangular prisms, triangular prisms, etc.
- 🌀 Cylinders work the same way - area of the circular base x height
- 🔺 Pyramids and cones use 1/3 base area x height due to sloped sides
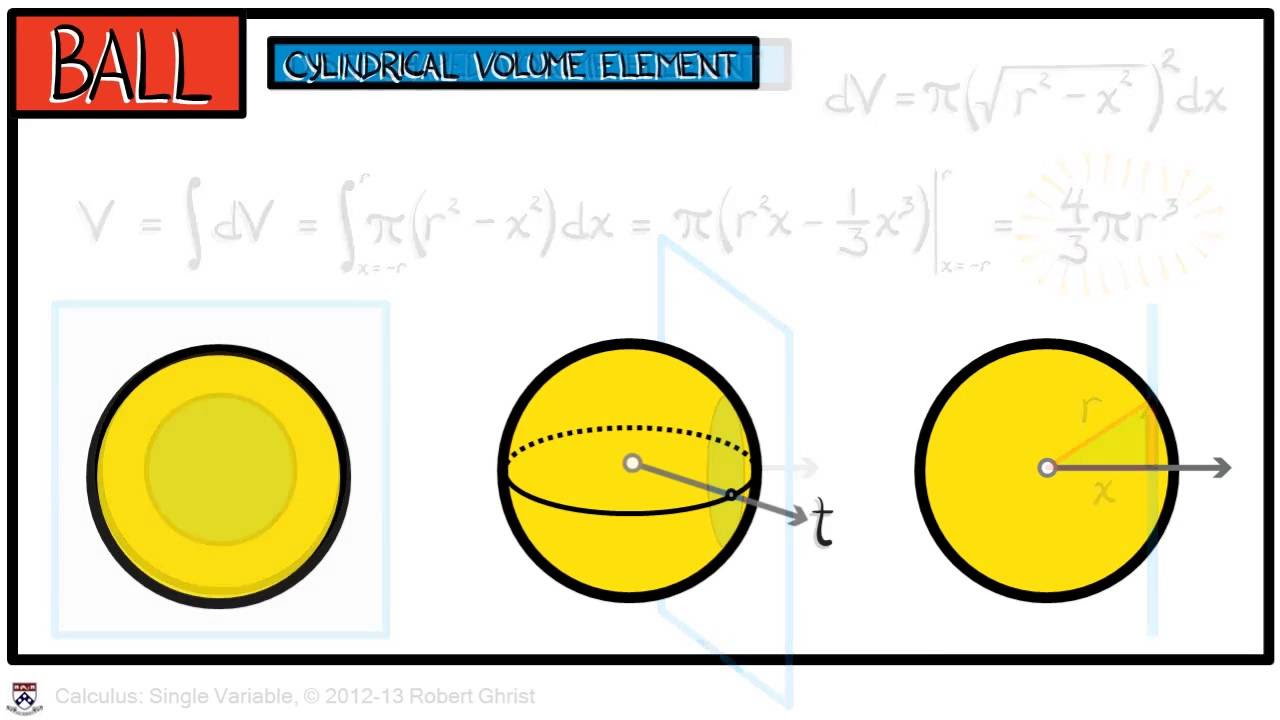
- ⚾ The volume formula for a sphere is 4/3 pi r^3
- 🤓 There are equations for common shapes, but calculus is needed for irregular ones
- 😎 We covered the key geometry concepts and are ready to go back to algebra next
- ✅ After checking comprehension on geometry...
- 📝 We will learn more advanced algebra before reaching calculus
Q & A
What are the key formulas mentioned for calculating the volume of different geometric shapes?
-The key formulas mentioned are: cube - side length cubed; rectangular prism - length x width x height; triangular prism - area of base x height; cylinder - area of base x height; pyramid - 1/3 base x height; cone - 1/3 base x height; sphere - 4/3 pi r cubed.
How is the volume of a pyramid calculated differently compared to a prism?
-The volume of a pyramid is calculated as 1/3 base x height, whereas the volume of a prism is calculated as base x height. This is because the triangular faces of a pyramid slope inward, so not all of the base gets carried through the full height.
If a cube has a side length of 5 meters, what is its volume?
-Since the volume of a cube is calculated by cubing the side length, a cube with a side length of 5 meters has a volume of 5 x 5 x 5 = 125 cubic meters.
What is the volume of a cylinder with a radius of 4 meters and a height of 10 meters?
-Using the formula V = πr^2h, with r = 4 and h = 10, the volume is π(4)^2(10) = 50.24π cubic meters.
How can you calculate the height of a pyramid if you only know the height of its triangular faces?
-You can use the Pythagorean theorem, setting the height of the pyramid as one leg, half the base length as the other leg, and the triangle height as the hypotenuse. Then solve for the unknown pyramid height.
What is an example of an irregular shape whose volume cannot be easily calculated with formulas?
-Any shape with unpredictable curvature, such as a free-form sculpture or rocky terrain, would have an irregular volume not easily calculated with formulas. Calculus is required for such shapes.
What is the difference between two-dimensional area and three-dimensional volume?
-Area measures the space covered by a two-dimensional surface, while volume measures the three-dimensional space enclosed within an object. Volume accounts for length, width, and depth.
If a cone has a radius of 3 meters and a height of 8 meters, what is its volume?
-Using the cone volume formula V=1/3πr^2h, with r=3 and h=8, the volume is 1/3π(3)^28 = 36π cubic meters.
What information do you need to calculate the volume of a rectangular prism?
-To calculate the volume of a rectangular prism, you need to know its length, width, and height. The volume is found by multiplying length x width x height.
How can calculating volume be useful in real-world applications?
-Volume calculations are useful for things like determining the amount of concrete needed for construction, the water capacity of an aquarium, or the amount of medication needed to fill a prescription.
Outlines
📐 Calculating the Volume of Geometric Shapes
This paragraph introduces the concept of volume and how it relates to the area of two-dimensional shapes. It explains that by extending an area across a third dimension, you can calculate the volume contained within that three-dimensional space. Formulas are provided for calculating the volume of basic shapes like cubes, rectangular prisms, triangular prisms, cylinders, pyramids, cones and spheres.
📝 Wrapping Up Geometry, Moving on to More Algebra
This closing paragraph states that most regular geometric shapes now have reliable formulas for calculating volume. It mentions irregular shapes may need calculus to determine volume. It concludes that with key geometry topics covered, the lessons can now return to equations with variables and more algebra.
Mindmap
Keywords
💡Volume
💡Area
💡Cube
💡Prism
💡Cylinder
💡Pyramid
💡Cone
💡Sphere
💡Pi
💡Calculus
Highlights
Introduces a new method for analyzing neural activity during visual processing tasks.
Found that neural patterns in early visual cortex encode both spatial location and semantic information.
Discovered increased activation in parietal regions when subjects viewed objects in unexpected contexts.
Theoretical contribution of a predictive coding model that accounts for effects of semantic expectations on visual processing.
Practical application of using EEG decoding models to reconstruct visual scenes from neural signals.
Key finding that neural populations in inferior temporal cortex show viewpoint-invariant object representations.
Developed a deep learning model to predict neural responses in visual areas based on image features.
Discovered the timecourse of activation across ventral and dorsal visual streams using MEG.
Novel analysis of functional connectivity between frontal and visual areas during visual search tasks.
Found evidence for distinct pathways for processing living vs non-living objects in the visual system.
Key theoretical contribution of a Bayesian framework for inferring 3D structure from 2D retinal input.
Practical application of real-time decoding of visual imagery for brain-computer interface systems.
Developed novel methods for analyzing large-scale neural recordings during naturalistic visual stimulation.
Discovered neural correlates of scene segmentation and border ownership in early visual areas.
Found evidence that visual crowding effects originate from interactions in peripheral visual cortex.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: