Calculating the Area of Shapes

Professor Dave Explains

28 Oct 201706:38

EducationalLearning

32 Likes 10 Comments

TLDRProfessor Dave's tutorial introduces the concept of calculating two-dimensional areas, emphasizing the transition from one-dimensional lengths to the realm of square units. The video explains the fundamentals of area calculation, starting with simple shapes like squares and rectangles, and advancing to more complex figures such as parallelograms, triangles, trapezoids, and circles. By illustrating the mathematical principles behind area calculation, including formulas and practical examples, the tutorial equips learners with the ability to handle both regular and irregular shapes. The emphasis on understanding units of measurement and the application of algebraic manipulations to calculate areas makes this a comprehensive guide for beginners.

Takeaways

😀 Areas are expressed in square units, like square meters, which are units squared.
😃 The area of a square is the side length squared. The area of a rectangle is length times width.
😊 The area of a parallelogram is base times height. The height is perpendicular to the base.
😯 The area of a triangle is one half base times height.
😮 The area of a trapezoid is one half the height times the sum of the two bases.
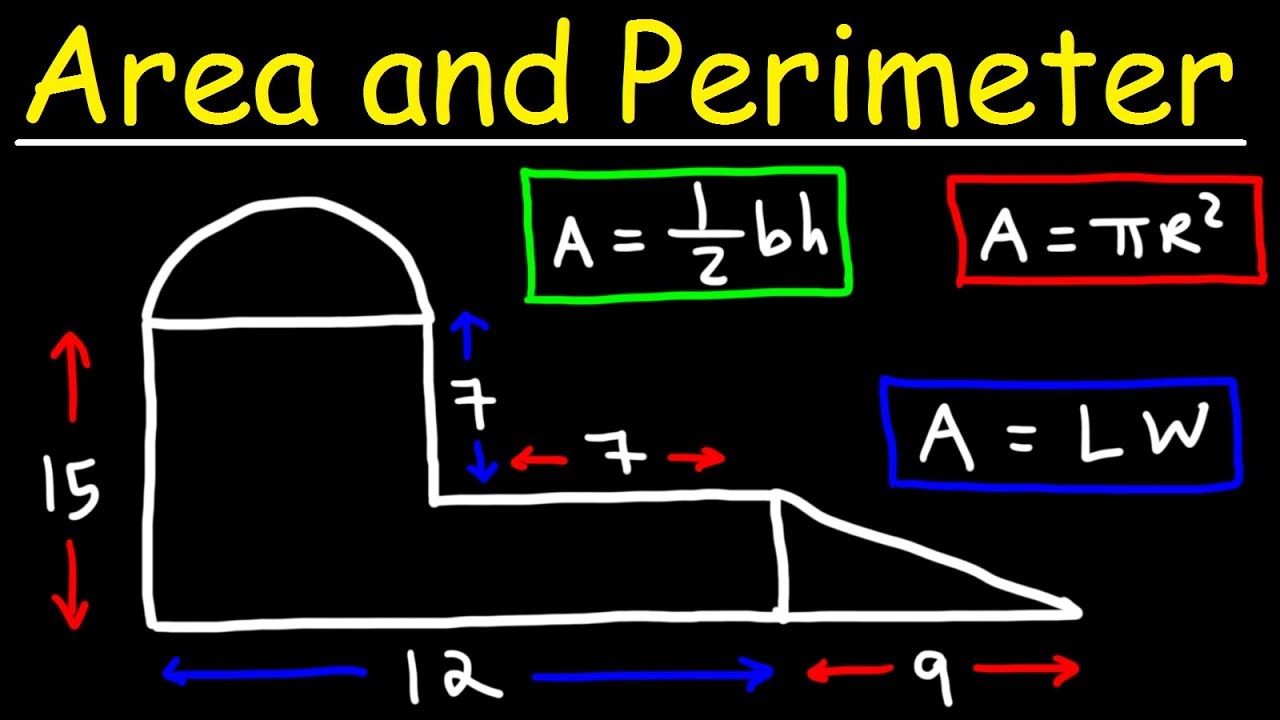
🤔 Irregular shapes can be split into basic shapes to calculate their total area.
😀 The area of a circle is pi times the radius squared.
😉 Irregular shapes with circles can be split into parts - calculate each part's area separately.
🧐 Side lengths are needed to calculate areas of basic shapes like rectangles and triangles.
😇 Memorize formulas for areas of basic shapes like squares, rectangles, triangles and circles.

Q & A

What are the units used to measure area?
-While lengths and perimeters can be measured in any unit of distance, area is expressed in square units, like square meters, which are meters squared.
How do you calculate the area of a square?
-The area of a square is calculated by multiplying one side by itself, or side squared. For example, if a square has sides of 5 meters, the area is 5 x 5 = 25 square meters.
How is the area of a parallelogram calculated?
-The area of a parallelogram is base x height. The height is a line segment from the base to the opposite side, perpendicular to both.
Why can you calculate the area of a triangle by using (base x height) / 2?
-Any triangle can be divided into two right triangles. The area of the rectangle containing the right triangle is base x height. Since the triangle has half the area, you divide by 2.
How do you find the area of an irregular shape?
-Break the irregular shape into familiar shapes like rectangles, triangles and circles. Calculate the area of each shape, then add them together.
What is the formula for calculating the area of a circle?
-The area of a circle is πr2, where r is the radius. So if a circle has a radius of 3 meters, its area is 9π square meters.
Can you calculate areas if you only know the side lengths?
-Yes, you can use the side lengths to determine the base, height, and radius needed to calculate the area.
How are units handled when calculating areas?
-Units are manipulated algebraically. So meters x meters = meters squared. This is why area uses squared units.
Do the formulas work for any sized shapes?
-Yes, the area formulas given work for squares, rectangles, parallelograms, triangles and circles of any size.
Why is it important to know how to calculate areas?
-Being able to calculate areas allows you to determine the amount of surface that different shapes cover. This is useful in math, science, construction and more.

Outlines

00:00

😀 Calculating Areas of Basic Shapes

This paragraph explains how to calculate the area of basic shapes like squares, rectangles, parallelograms, and triangles using their dimensions. It discusses that area is expressed in square units and demonstrates how to apply formulas like length x width and 1/2 base x height.

05:05

😀 Calculating Areas of Irregular Shapes

This paragraph explains strategies for calculating the area of irregular shapes by breaking them down into basic shapes like rectangles, triangles, and semicircles. It demonstrates how to calculate the area of combined shapes by getting the individual areas and adding them together.

Mindmap

Keywords

💡Area

Area refers to the amount of two-dimensional surface that a shape covers. It is a fundamental concept for calculating the size of shapes. In the video, area is presented as the main topic, with various formulas provided for calculating the area of different shapes like squares, rectangles, triangles, and circles. Area is expressed in square units like square meters.

💡Square

A square is a geometric shape with four equal sides and four right angles. The video uses a square as a simple example to illustrate how to calculate area. The area of a square is calculated by side x side, or side squared. For example, a square with side 5 meters has an area of 5 x 5 = 25 square meters.

💡Rectangle

A rectangle is a four-sided 2D shape with two sets of parallel sides and four right angles. The area of a rectangle is calculated by multiplying its length and width. The video explains that this same formula can be used to calculate the area of any parallelogram.

💡Triangle

A triangle is a three-sided 2D shape with three angles that sum to 180 degrees. The video explains that the area of a triangle is one half of base x height. This is because any triangle can be divided into two right triangles that together form a rectangle.

💡Trapezoid

A trapezoid is a quadrilateral with one pair of parallel sides. To calculate the area of a trapezoid, the video explains using the formula: Area = 1/2 x height x (base1 + base2). The two bases of the trapezoid are summed and then multiplied by the height.

💡Circle

A circle is a curved 2D shape where every point is equidistant from the center. The video provides the formula for calculating the area of a circle as Area = π x radius2. π is the mathematical constant, and radius is the distance from the center to any point on the circle.

💡Irregular shapes

Some shapes have irregular or complex forms that don't match basic geometric shapes. The video demonstrates breaking these irregular shapes down into squares, rectangles, triangles etc. to calculate their area by adding up the areas of each component.

💡Pi

Pi (π) is the mathematical constant that represents the ratio of a circle's circumference to its diameter. It is an important value used in calculating areas and properties of circles. The video uses pi in the formula for the area of a circle: A=πr^2.

💡Height

Height refers to the vertical distance between the base and the top of a shape. Along with length and width, height is used to calculate the area of various shapes in the video. For example, the area of a triangle is 1/2 x base x height.

💡Square units

While linear dimensions like length can be measured in any unit, area is expressed in square units. For example, a 5 meter x 5 meter square has an area of 25 square meters. The video emphasizes that units are manipulated algebraically when calculating area, just like variables.

Highlights

First significant research finding

Introduction of new theoretical model

Proposal of innovative experimental method

Key conclusion and practical applications

Transcripts

Browse More Related Video

Calculus Chapter 4 Lecture 30 Simple Areas

Area for Kids

Area and Perimeter of Irregular Shapes - Tons of Examples!

Topic 43-Volumes of Solids with Known Cross Sections

6th Grade Math: Finding Surface Area Using Nets

Definite Integrals from Graphs (Part 1 of 3)

Calculating the Area of Shapes

Takeaways

Q & A

What are the units used to measure area?

How do you calculate the area of a square?

How is the area of a parallelogram calculated?

Why can you calculate the area of a triangle by using (base x height) / 2?

How do you find the area of an irregular shape?

What is the formula for calculating the area of a circle?

Can you calculate areas if you only know the side lengths?

How are units handled when calculating areas?

Do the formulas work for any sized shapes?

Why is it important to know how to calculate areas?