Free body diagram sine and cosine components
TLDRThe video script explains the process of drawing a Freebody diagram and breaking down the forces into sine and cosine components. It uses the example of a box on an inclined plane to illustrate how to identify and resolve the forces acting on an object, such as gravity (mg), static friction, and the normal force (N). The script emphasizes the importance of correctly identifying the angle (theta) for the force components and suggests using limits to verify the accuracy of the chosen angle, ensuring that the force components align with the physical situation described.
Takeaways
- 📚 The process of breaking down a free body diagram into sine and cosine components is a common challenge in physics.
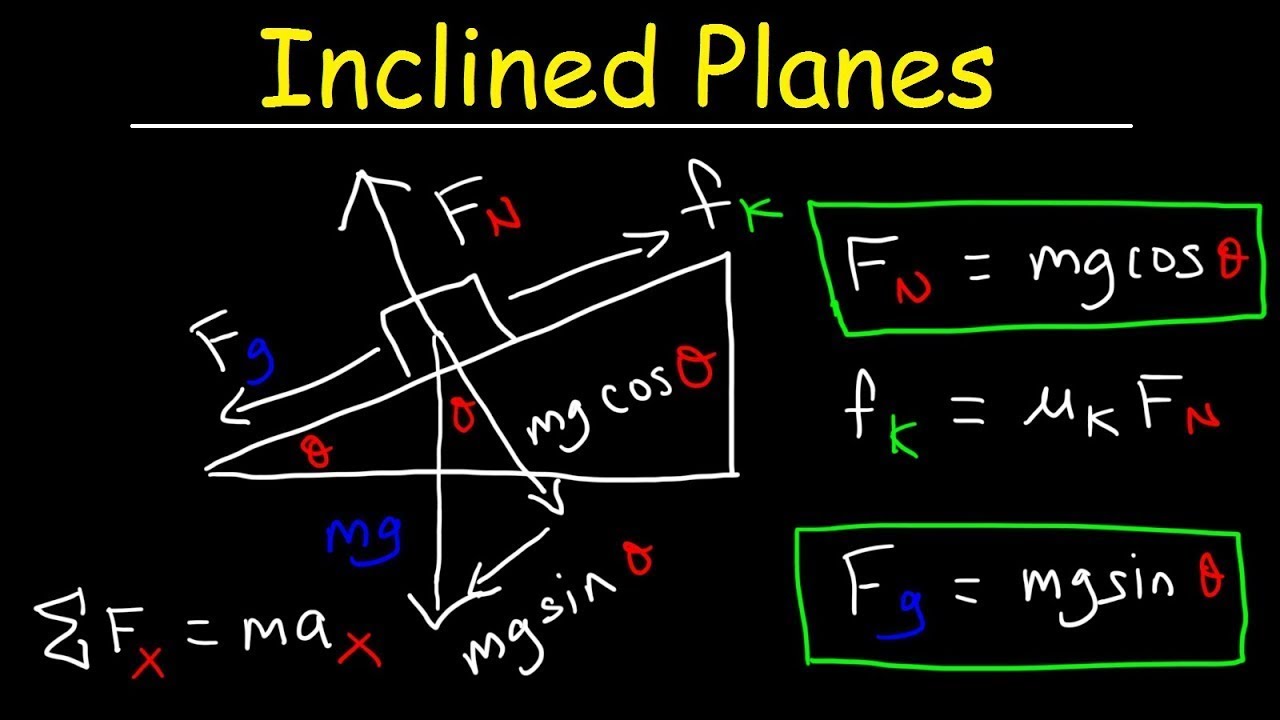
- 🎯 For a box on an inclined plane, the main forces acting on it are gravity (mg), static friction, and the normal force (N).
- 📐 Gravity acting on the box is represented as mg and can be decomposed into two components: mg sine theta (parallel to the incline) and mg cosine theta (perpendicular to the incline).
- 🔄 To determine the correct angle theta, one can make an educated guess and then verify it by examining the limits of the situation.
- 🌟 When theta approaches zero degrees, the force parallel to the incline (mg sine theta) should approach zero, while the force perpendicular to the incline (mg cosine theta) should approach mg.
- 🤔 The verification process involves using trigonometric principles and geometric understanding to confirm the accuracy of the initial guess.
- 📊 The correct free body diagram is essential for accurately analyzing the forces acting on an object in a physics problem.
- 🧠 Understanding the principles of SOHCAHTOA (Sine is Opposite/Hypotenuse, Cosine is Adjacent/Hypotenuse, etc.) is crucial for breaking down vectors into components.
- 🔧 Static friction acts in the opposite direction to the potential movement of the object, which in this case is up the incline to the left.
- 📚 The normal force is the reaction force from the inclined plane and acts perpendicular to the surface.
- 🎓 The ability to decompose forces into components is a fundamental skill in problem-solving for physics problems involving inclined planes.
- 💡 Always verify your work by considering the physical implications and limits of the forces involved to ensure the accuracy of your free body diagram.
Q & A
What is the basic problem discussed in the transcript?
-The basic problem discussed is breaking down a free body diagram into sine and cosine components, specifically for a box on an inclined plane.
What are the forces acting on the box in the example given?
-The forces acting on the box are gravity (mg), static friction, and the normal force (N).
How is the force of gravity (mg) represented in the free body diagram?
-Gravity (mg) is represented as a downward force acting on the box.
What direction is the static friction force in relation to the inclined plane?
-The static friction force is acting upward and to the left, opposing the motion down the slope.
What is the normal force (N) in the context of the inclined plane?
-The normal force (N) is the force exerted by the inclined plane upward on the box, perpendicular to the surface of the plane.
Why is it necessary to break the force of gravity (mg) into components?
-It is necessary to break mg into components because it is not aligned with the right angles in the free body diagram, and doing so helps in analyzing the forces acting along and perpendicular to the inclined plane.
How are the components of the gravitational force (mg) determined?
-The components are determined using trigonometry, where mg sine theta represents the force down the incline and mg cosine theta represents the force into the incline.
What is the significance of the angle theta in the context of the free body diagram?
-Theta represents the angle between the gravitational force (mg) and the horizontal component of the force acting along the inclined plane.
How can you verify if your guess for the angle theta is correct?
-You can verify the guess by considering the limits, such as when theta goes to zero degrees, and checking if the resulting forces match the expected conditions for that limit.
What happens to the force components when theta approaches zero degrees?
-When theta approaches zero degrees, the force down the incline (mg sine theta) approaches mg, and the force into the incline (mg cosine theta) approaches zero, since cosine of zero is 1.
What is the role of trigonometric functions in decomposing forces?
-Trigonometric functions, specifically sine and cosine, are used to decompose a vector like the gravitational force into its perpendicular and parallel components relative to the inclined plane.
Outlines
📚 Understanding Freebody Diagrams with Sine and Cosine Components
This paragraph introduces the concept of breaking down a free body diagram into its sine and cosine components, a common challenge for students. It uses the example of a box on an inclined plane to illustrate the forces at work, including gravity (mg), static friction, and the normal force (n). The speaker guides the audience through identifying these forces and explains the need to redraw the forces at right angles for clarity. The paragraph emphasizes the importance of correctly identifying the angle (theta) and using trigonometric relationships (sohcahtoa) to break down the gravitational force into components perpendicular and parallel to the incline.
🔍 Validating the Freebody Diagram through Limits
The second paragraph delves into the method of validating the guess made about the angle (theta) in the free body diagram. It explains that by examining the limits, such as when the angle goes to zero degrees, one can confirm the correctness of the guess. The speaker uses the limit of theta approaching zero to show that the force down the incline should equal the weight of the box (mg), and the force into the incline should approach zero, confirming the use of cosine and sine functions. The paragraph highlights the practical approach of using limits to verify the accuracy of the free body diagram and the significance of trigonometry in physics problem-solving.
Mindmap
Keywords
💡Freebody diagram
💡Sine and Cosine components
💡Inclined plane
💡Gravity (mg)
💡Static friction
💡Normal force
💡Trigonometry
💡Limits
💡Vector resolution
💡SoH-CaH-ToA
💡Force analysis
Highlights
The process of breaking down a free body diagram into sine and cosine components is a common struggle for students.
A basic physics problem is used as an example: a box on an inclined plane.
The free body diagram initially includes forces acting on the box such as gravity (mg) and static friction.
The normal force (N) is also acting on the box when it is on an inclined plane.
To simplify the diagram, forces need to be redrawn at right angles to each other.
Gravity (mg) is the force that needs to be broken into components since it is not aligned with the other forces.
The components of gravity are determined using trigonometry: mg sine theta for the force down the incline and mg cosine theta for the force into the incline.
The correct orientation of theta is verified by considering the limits, such as when theta approaches zero degrees.
When theta approaches zero, the force down the incline should approximate mg, which helps confirm the correct angle orientation.
The use of sohcahtoa (sine is opposite over hypotenuse, cosine is adjacent over hypotenuse) is mentioned as a mnemonic for trigonometric relationships.
A practical approach to determining the correct angle orientation is suggested: make an educated guess and then test it against known limits.
The importance of verifying the guess with limits is emphasized, as incorrect assumptions can lead to errors in the analysis.
The concept of a free body diagram is fundamental in understanding the forces at work on an object.
Inclined planes are a classic scenario for demonstrating the application of free body diagrams in physics.
Static friction is an important force to consider when an object is at rest on a surface.
The normal force is a reaction force that acts perpendicular to the surface of contact.
Trigonometric principles are essential for resolving vector components in physics problems.
The process of breaking down forces into components involves both vector analysis and trigonometry.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: