Breaking down forces for free body diagrams | AP Physics 1 | Khan Academy

Khan Academy
26 Mar 201809:22
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses the concept of a free-body diagram, a tool used in physics to visualize and analyze the forces acting on an object. The instructor uses a 10-newton block on a frictionless surface to explain how gravity and the normal force balance out, resulting in no acceleration. The scenario then evolves with the addition of a 20-newton force at a 60-degree angle, which necessitates breaking down the force into horizontal and vertical components using trigonometry. This analysis allows for the prediction of the block's motion, highlighting the practical application of free-body diagrams in understanding the dynamics of objects.

Takeaways
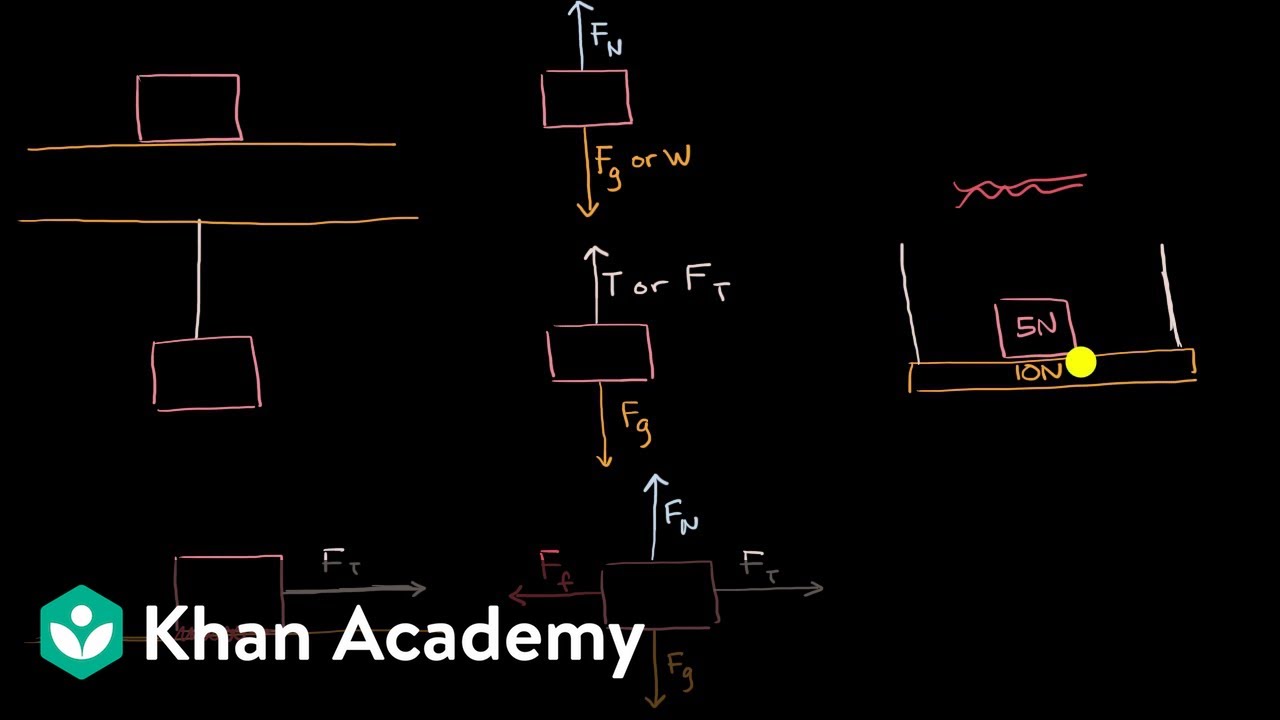
  • 📐 A free-body diagram is a tool used in physics to visualize and analyze the forces acting on an object in isolation.
  • 🔽 The weight of an object, which is the force of gravity acting on it, always acts vertically downward and can be represented as a vector in the diagram.
  • 🔄 When an object is in equilibrium, the net force acting on it is zero, meaning all forces are balanced.
  • 🏗️ The normal force is the reaction force exerted by a surface on an object, acting perpendicularly to the surface and opposite in direction to the weight.
  • 📐️ In a free-body diagram, vectors are typically shown originating from the center of the object for clarity.
  • 🔄️ To analyze forces acting at an angle, they must be resolved into their horizontal and vertical components using trigonometry.
  • 📐️ The horizontal component of a force is calculated as the product of the force's magnitude and the cosine of the angle (F cos θ).
  • 🔄️ The vertical component of a force is calculated as the product of the force's magnitude and the sine of the angle (F sin θ).
  • 📊 Knowing the trigonometric values for common angles (0°, 30°, 45°, 60°, 90°) is beneficial for quickly resolving forces in a free-body diagram.
  • 🚀 The net force on an object determines its acceleration according to Newton's second law of motion (F = ma).
  • 🎯 Free-body diagrams are essential for predicting the motion of an object under the influence of various forces.
Q & A

  • What type of surface is described in the beginning of the transcript?

    -A hard, flat, frictionless surface is described.

  • What is the weight of the block mentioned in the script?

    -The block weighs 10 newtons.

  • What is the significance of a free-body diagram?

    -A free-body diagram is used to represent all the forces acting on an object, helping to analyze its motion without the influence of its surroundings.

  • How many newtons is the force applied to the block at a 60-degree angle?

    -The force applied is 20 newtons.

  • What are the two typical ways of drawing a free-body diagram?

    -The two typical ways are: 1) drawing vectors originating out of the center of the object, and 2) drawing vectors from outside the body.

  • What is the horizontal component of the 20-newton force acting at a 60-degree angle?

    -The horizontal component is 10 newtons (20 N * cos(60 degrees) = 10 N).

  • What is the vertical component of the 20-newton force acting at a 60-degree angle?

    -The vertical component is 10√3 newtons (20 N * sin(60 degrees) ≈ 10 * √3 N).

  • What happens to the block when only the weight and normal force are acting on it?

    -The block remains stationary as there is no net force acting on it, meaning the forces are balanced.

  • What is the net force acting on the block after the 20-newton force is applied at a 60-degree angle?

    -The net force is 10 newtons to the right, as the upward normal force balances the downward forces, leaving only the horizontal component of the applied force unopposed.

  • What will be the block's acceleration according to Newton's second law after the 20-newton force is applied?

    -According to Newton's second law (F = ma), the block will accelerate to the right with an acceleration of 1 m/s² (assuming the mass of the block is 1 kg, and the net force is 10 N).

  • Why is it important to break down forces into their horizontal and vertical components?

    -Breaking down forces into components simplifies the analysis by allowing us to consider the effects of the force in the context of the object's surface, which helps in determining the net force and predicting the object's motion.

Outlines
00:00
📚 Introduction to Free-Body Diagrams

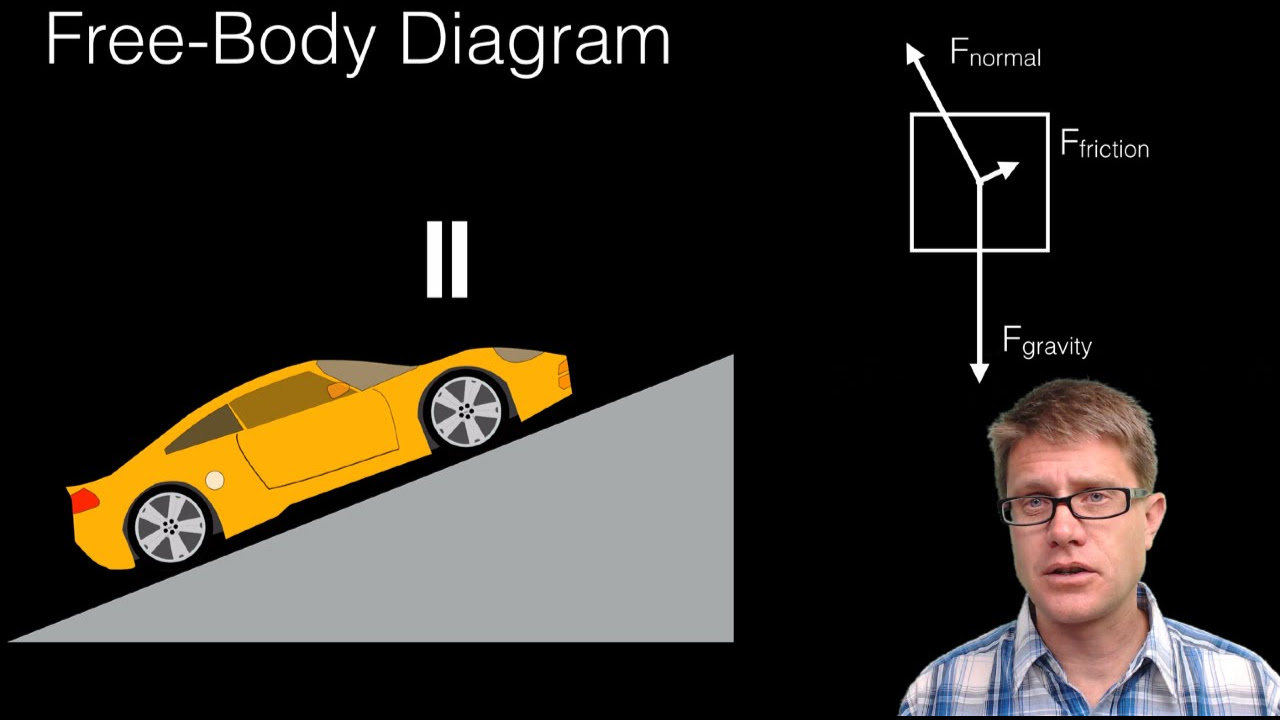
The instructor introduces the concept of a free-body diagram, which is a tool used to visualize all the forces acting on a single object. The example given involves a 10-newton block resting on a frictionless surface. The instructor explains that the block is subject to two forces: the downward force of gravity and the upward normal force from the surface. The purpose of the free-body diagram is to analyze these forces to understand the object's state of motion or lack thereof. Two common ways of drawing such diagrams are briefly mentioned, with the emphasis on focusing on the object in question and ignoring the surroundings.

05:01
📐 Breaking Down Forces with Trigonometry

The instructor continues the discussion by introducing a scenario where an additional force is applied to the block at a 60-degree angle. The focus is on how to break down this force into its horizontal and vertical components using basic trigonometry. The explanation includes the formulas for calculating the components (F cosine theta for the horizontal component and F sine theta for the vertical component) and the specific values for the cosine and sine of 60 degrees. The new free-body diagram now includes the original forces and the components of the applied force, allowing for a prediction of the block's acceleration to the right due to the net force.

Mindmap
Keywords
💡Hard, flat, frictionless surface
A hard, flat, frictionless surface is an idealized physical model used in physics to describe a surface that is perfectly smooth and offers no resistance to sliding objects. In the context of the video, this surface is where the block is resting and it is essential for understanding the forces acting on the block, as it defines the absence of frictional forces.
💡Block
In the context of this video, a 'block' refers to a simple geometric object used in physics problems to represent a solid body with mass. The block in the video has a weight of 10 newtons and is used to illustrate the principles of statics and dynamics, particularly the forces acting upon it at rest and when subjected to an external force.
💡Weight
Weight is the force exerted on an object due to gravity. It is calculated as the product of the object's mass and the acceleration due to gravity. In the video, the block has a weight of 10 newtons, which represents the downward force exerted by gravity on the block.
💡Free-body diagram
A free-body diagram is a graphical representation used in physics to show all the forces acting on an object. It simplifies the analysis of physical systems by isolating the object of interest and depicting only the external forces acting upon it, without including any surrounding objects or environment.
💡Normal force
The normal force is the perpendicular force exerted by a surface on an object in contact with it. It acts in the opposite direction to the force of gravity (or the weight of the object) and prevents the object from passing through the surface. In the video, the normal force is the force exerted by the frictionless surface on the block to counteract its weight.
💡Acceleration
Acceleration is the rate of change of velocity of an object with respect to time. It is a vector quantity that describes how quickly an object speeds up, slows down, or changes direction. In the context of the video, the absence of acceleration indicates that the net force acting on the block is zero, as per Newton's first law of motion.
💡Force components
Force components refer to the individual horizontal and vertical parts of a force that acts at an angle to the horizontal. By breaking down a force into its components, one can analyze the effects of the force in the horizontal and vertical directions separately. In the video, the applied force is decomposed into horizontal and vertical components to understand its impact on the block's motion.
💡Trigonometry
Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles, particularly right-angled triangles. In physics, trigonometry is often used to resolve forces into their components and to calculate distances and angles in problems involving vectors. The video uses basic trigonometry to calculate the horizontal and vertical components of the applied force.
💡Net force
Net force, also known as the resultant force, is the vector sum of all the individual forces acting on an object. It determines the overall force that affects the object's motion according to Newton's second law of motion. In the video, the net force on the block is calculated by considering the balance of forces acting in the vertical direction and the unbalanced force in the horizontal direction.
💡Acceleration to the right
Acceleration to the right refers to the increase in velocity in the rightward direction of an object. According to Newton's second law of motion, an unbalanced force in a particular direction will cause an object to accelerate in that direction. In the video, the net force of 10 newtons to the right implies that the block will accelerate to the right.
Highlights

The concept of a free-body diagram is introduced as a tool to visualize and analyze the forces acting on an object.

A block on a hard, flat, frictionless surface is used as an example to demonstrate the forces at play when an object is in equilibrium.

The weight of the block is given as 10 newtons, representing the force of gravity acting on it.

A free-body diagram is drawn to show the downward force of gravity and the upward normal force that keeps the block from accelerating.

The normal force is equal in magnitude but opposite in direction to the force of gravity, resulting in no net force and thus no acceleration.

Another way to draw a free-body diagram is by showing vectors originating from outside the object.

A new force of 20 newtons at a 60-degree angle is applied to the block, prompting a reevaluation of the free-body diagram.

The applied force must be broken down into horizontal and vertical components to accurately represent its effect on the block.

Trigonometry is used to calculate the components of the force, with the horizontal component being F cosine theta and the vertical component F sine theta.

The cosine and sine values for 60 degrees are used to determine the magnitudes of the force components, which are 10 newtons and 10√3 newtons respectively.

The normal force is adjusted to counteract both the force of gravity and the vertical component of the applied force.

The net force acting on the block is calculated to be 10 newtons to the right, indicating that the block will accelerate in that direction.

The importance of knowing trigonometric values for common angles is emphasized for both trigonometry and physics applications.

The practical application of free-body diagrams is demonstrated in predicting the motion of an object based on the net forces acting upon it.

The use of free-body diagrams is highlighted as a fundamental technique in physics for analyzing static and dynamic situations.

The video provides a step-by-step guide on how to create and interpret free-body diagrams, which is essential for understanding physical systems.

The example illustrates the balance between applied forces and reaction forces, leading to either acceleration or equilibrium.

The video content is both educational and practical, offering a clear explanation of how forces interact and affect the motion of objects.

Transcripts

Browse More Related Video

GCSE Physics - Resultant Forces & Free Body Diagrams #42

High School Physics - Free Body Diagrams

Types of forces and free body diagrams | AP Physics 1 | Khan Academy

2022 Live Review 2 | AP Physics 1 | Understanding Forces and Newton’s Laws

Newton's Laws: Crash Course Physics #5

Free-Body Diagrams

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Physics ConceptsForce AnalysisFree-Body DiagramsGravityApplied ForceTrigonometryAccelerationStatic EquilibriumHard SurfaceFrictionless