Equations of Projectile Motion in Physics Explained - [1-4-6]

This paragraph introduces the concept of projectile motion, emphasizing that the equations used are the same as those for straight-line motion but applied to two dimensions (x and y). The speaker reassures the audience that despite the complexity of physics textbooks, the principles of projectile motion are straightforward. The core idea is that a curved path can be broken down into two separate motions: horizontal and vertical. The speaker uses the example of throwing a ball to illustrate this point, explaining that the motion can be thought of as a combination of horizontal movement and up-and-down movement. The importance of understanding this separation of motions is highlighted as it simplifies the application of known equations to each dimension separately.

In this paragraph, the focus is on the role of gravity in projectile motion. It explains that the acceleration due to gravity (g) acts only in the y-direction (downward), making it -9.8 m/s². The speaker clarifies that while the object follows a curved path, gravity affects only the vertical component of the motion. This means that the horizontal motion is unaffected by gravity, and the vertical motion is influenced solely by gravity. The speaker emphasizes that this separation of effects is crucial for solving projectile motion problems and encourages the audience to internalize this concept.

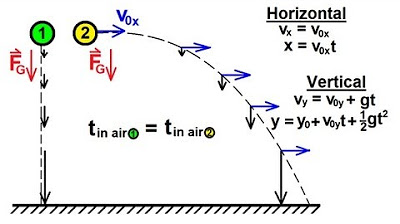
The speaker continues to elaborate on the impact of gravity on the vertical motion of a projectile. They explain that gravity acts purely downward, causing the object to accelerate at a rate of -9.8 m/s². The speaker uses the analogy of a ball thrown at an angle to illustrate that despite the curved path, the vertical motion is independent of the horizontal motion. They also describe an experiment where two balls are released from the same height, one thrown horizontally and the other dropped, and both hit the ground simultaneously, demonstrating that the time of flight is determined solely by the vertical motion, regardless of the horizontal motion.

This paragraph delves into the analysis of the x and y components of velocity during projectile motion. The speaker explains how the initial velocity (v_naught) can be broken down into horizontal (v_x) and vertical (v_y) components using trigonometric functions—cosine and sine, respectively. They illustrate that at the peak of the trajectory, the vertical velocity is zero, while the horizontal velocity remains constant. The speaker emphasizes that the horizontal component of velocity is unaffected by gravity, and the vertical component is influenced by gravity alone, changing over time due to the acceleration of -9.8 m/s².

The speaker transitions to applying one-dimensional motion equations to projectile motion. They reiterate that the same fundamental equations of motion apply, but they must be applied separately to the x and y components of motion. The speaker simplifies the process by stating that in the x-direction, there is no acceleration (ax = 0), and in the y-direction, the acceleration is equal to -g (ay = -9.8 m/s²). They also introduce the concept of using trigonometric functions to determine the x and y components of the initial velocity based on the launch angle. The speaker discourages memorizing additional equations and encourages understanding the underlying principles instead.

The speaker further explains the decomposition of the initial velocity into its x and y components using trigonometry. They clarify that the x-component of the initial velocity (v_naught_x) is given by the total initial velocity (v_naught) times the cosine of the launch angle (theta), and the y-component (v_naught_y) is v_naught times the sine of theta. The speaker emphasizes that these components are crucial for solving projectile motion problems and that understanding the separation of horizontal and vertical motions is key. They also highlight that the equations derived from these components are not new but are simply applications of the basic one-dimensional motion equations to each direction, with the appropriate acceleration values (0 for horizontal and -g for vertical).

The speaker concludes by reinforcing the main takeaway: the x and y components of projectile motion are independent and are solved using the same basic one-dimensional motion equations, with the x component having no acceleration and the y component having an acceleration due to gravity. The speaker advises against memorizing complex equations and instead encourages understanding the principles, which will help in solving problems effectively. They also mention that in most cases, the initial position is zero, which can further simplify the equations. The speaker invites the audience to follow them to the next lesson, where they will apply these concepts to solve a projectile motion problem.