Using Equations of Projectile Motion
TLDRThe transcript delves into the concept of projectile motion, emphasizing that it can be simplified by breaking it down into horizontal and vertical components. It explains that while the curved path of a projectile is influenced by gravity, the horizontal motion remains unaffected by this force. The core idea is that the equations for projectile motion are the same as those for one-dimensional motion, but applied separately to the X and Y directions. The transcript also touches on the parabolic path of projectiles and the independence of horizontal and vertical motions, using the example of a ball thrown at an angle to illustrate the principles. The lesson aims to demystify the complexity of projectile motion by relating it to familiar algebraic concepts and encouraging a deeper understanding of the underlying physics.
Takeaways
- 📐 Projectile motion can be broken down into two separate components: horizontal motion and vertical motion.
- 🎾 The horizontal motion is unaffected by gravity and continues at a constant velocity.
- 🚀 The vertical motion is influenced by gravity, causing the object to accelerate downwards at a rate of 9.8 m/s².
- 📈 The equations of motion for horizontal and vertical directions are the same as those for one-dimensional motion, with no acceleration in the horizontal direction (a_x = 0) and an acceleration due to gravity in the vertical direction (a_y = -g).
- 🌐 The trajectory of a projectile follows a parabolic path, which is a result of the combined horizontal and vertical motions.
- 🔄 The components of the initial velocity can be determined using trigonometric functions: V_x = V₀ * cos(θ) and V_y = V₀ * sin(θ), where V₀ is the initial velocity and θ is the launch angle.
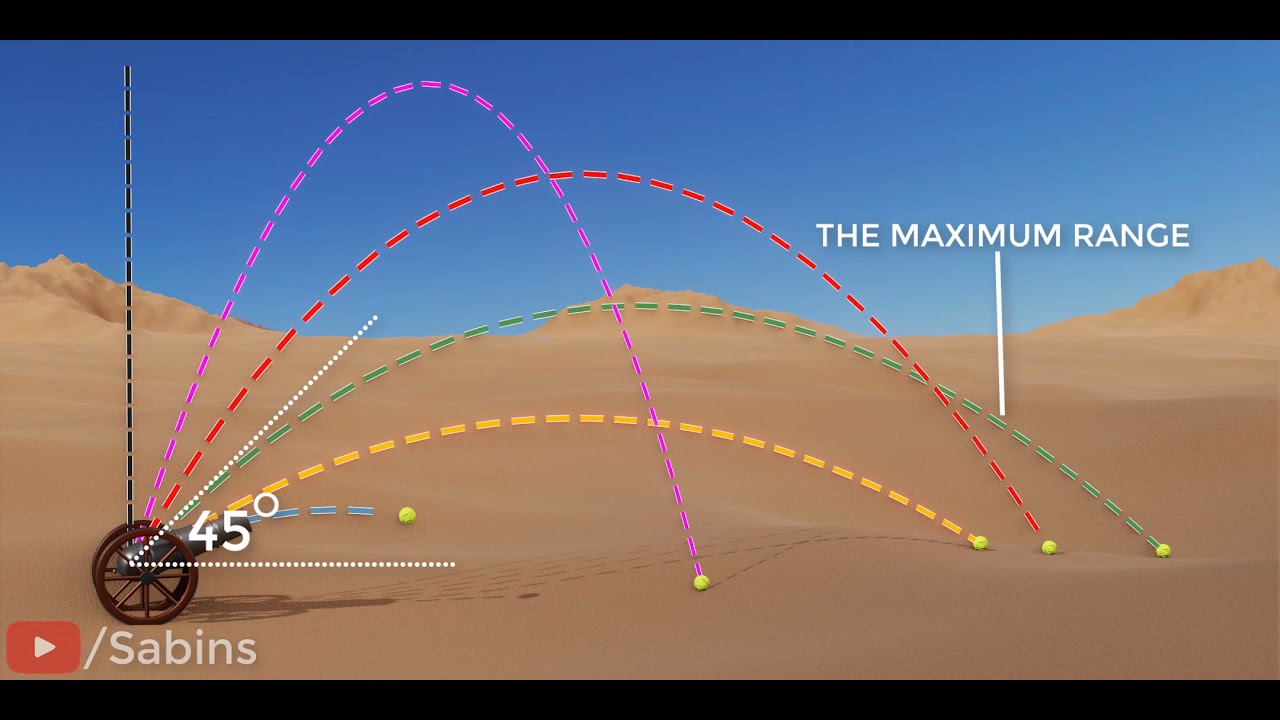
- 🎢 The maximum height reached by the projectile can be calculated using the vertical motion equations, considering the initial vertical velocity and the acceleration due to gravity.
- 🏆 Understanding the independence of horizontal and vertical motions is crucial for solving projectile motion problems.
- 📚 The key to solving projectile motion problems is to apply the equations of motion separately to the horizontal and vertical components of the motion.
- 🎥 The video script emphasizes the importance of visualizing the motion components separately and not being overwhelmed by the curved path of the projectile.
Q & A
What is the core principle of projectile motion?
-The core principle of projectile motion is that a curved path can be broken down into two separate motions: horizontal motion and vertical motion.
How does the curved path of a projectile motion relate to algebraic parabolas?
-The curved path of a projectile motion is a parabolic path, which is the same shape as the algebraic parabolas studied in algebra, such as y = x^2. This is because the motion traces out a path in a gravitational field, which follows parabolic equations.
What are the two components of projectile motion and how do they interact?
-The two components of projectile motion are the horizontal motion and the vertical motion. These components are independent of each other; the horizontal motion continues at a constant speed without being affected by gravity, while the vertical motion is influenced by gravity, causing it to accelerate downwards.
Why is it beneficial to break down projectile motion into horizontal and vertical components?
-Breaking down projectile motion into horizontal and vertical components simplifies the problem-solving process. The horizontal motion is much simpler as it lacks the influence of gravity, making calculations easier compared to the vertical motion, which includes the acceleration due to gravity.
What is the role of gravity in the vertical component of projectile motion?
-Gravity acts purely vertically in the downward direction with an acceleration of -9.8 m/s^2. It affects the vertical component of the motion by causing the object to accelerate downwards, slowing down as it rises and speeding up as it falls.
How does the initial velocity of a projectile affect its motion?
-The initial velocity of a projectile, along with the launch angle, determines the path of the projectile. It influences both the horizontal and vertical components of the motion, affecting how high the object will go and how far it will travel before hitting the ground.
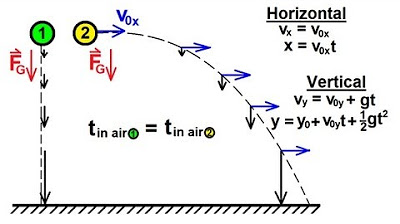
What happens to two objects released simultaneously from the same height, one thrown horizontally and the other dropped?
-Both objects will hit the ground at the same time. The horizontal motion does not affect the time it takes for the objects to reach the ground, as gravity acts only in the vertical direction.
How can the equations of motion be applied to projectile motion?
-The equations of motion can be applied to projectile motion by separating them into horizontal (x-direction) and vertical (y-direction) components. In the horizontal direction, there is no acceleration due to the absence of gravity, while in the vertical direction, the acceleration is equal to the acceleration due to gravity (-9.8 m/s^2).
What are the trigonometric relationships used to break down the initial velocity of a projectile into its horizontal and vertical components?
-The horizontal component of the initial velocity is given by the total velocity times the cosine of the launch angle (V_x = V₀ * cos(θ)), and the vertical component is given by the total velocity times the sine of the launch angle (V_y = V₀ * sin(θ)).
Why is it important to understand that the horizontal and vertical motions in projectile motion are independent?
-Understanding the independence of the horizontal and vertical motions is crucial for solving projectile motion problems. It allows for the separation of the motion into simpler, one-dimensional components, facilitating the application of the equations of motion and the calculation of various aspects of the motion, such as range, height, and time of flight.
Outlines
🚀 Introduction to Projectile Motion
The speaker introduces the concept of projectile motion, emphasizing that it may seem complex but can be understood by breaking it down into two separate motions along the X and Y axes. The core principle is that a curved path, such as that of a thrown ball, can be analyzed as a combination of horizontal motion and vertical motion. The equations used for projectile motion are the same as those for basic motion, but applied separately to each direction.
📐 Understanding the Components of Motion
The speaker explains that the motion of a projectile can be separated into horizontal and vertical components. The horizontal motion continues at a constant velocity because there is no acceleration in the horizontal direction (gravity only acts vertically). The vertical motion, however, is affected by gravity, causing the object to follow a parabolic path. The speaker uses the example of throwing a rock to illustrate how the path can be analyzed in terms of separate horizontal and vertical motions.
🎯 Applying the Equations of Motion
The speaker discusses how to apply the equations of motion to projectile motion. By considering the horizontal (X) and vertical (Y) directions separately, the same equations used for motion without gravity can be applied. The speaker emphasizes that the horizontal motion is unaffected by gravity, while the vertical motion is accelerated by gravity (with an acceleration of -9.8 m/s²). The explanation includes a visual representation of the parabolic path and the concept of initial velocity as a vector with components along the X and Y axes.
🌐 The Independence of Horizontal and Vertical Motion
The speaker illustrates the independence of horizontal and vertical motion using an experiment where two balls are released simultaneously: one is dropped, and the other is thrown horizontally. Despite the different paths, both balls hit the ground at the same time, demonstrating that the horizontal motion does not affect the vertical motion (or time of flight). The speaker emphasizes that the vertical and horizontal components of motion are completely independent and should be analyzed separately when solving projectile motion problems.
📐 Further Analysis of Projectile Motion
The speaker continues to dissect projectile motion, focusing on the components of velocity along the path of the projectile. The speaker explains that the velocity vector can be broken down into horizontal (Vx) and vertical (Vy) components, which change independently over time due to gravity's influence. The speaker uses a series of diagrams to show how the vertical component of velocity decreases due to gravity while the horizontal component remains constant, resulting in the curved trajectory of the projectile.
📝 Equations of Motion for Projectile Motion
The speaker provides a detailed explanation of how to apply the equations of motion to projectile motion. The speaker reiterates that the basic equations of motion from one-dimensional motion can be applied to both the X and Y components of projectile motion, with the only difference being the inclusion of gravity's acceleration (-9.8 m/s²) in the vertical direction. The speaker also addresses common misconceptions about the need to memorize additional equations, emphasizing that understanding the principles and applying them correctly is more important than rote memorization.
🔄 Incorporating Launch Angle into Motion Analysis
The speaker explains how to incorporate the launch angle into the analysis of projectile motion. Using trigonometry, the speaker shows how the initial velocity can be分解 into horizontal (Vx) and vertical (Vy) components using the cosine and sine of the launch angle (theta). The speaker then substitutes these components into the equations of motion for both the X and Y directions, demonstrating how to solve for the position and velocity of the projectile at any given time after launch.
Mindmap
Keywords
💡Projectile Motion
💡X and Y Directions
💡Acceleration of Gravity
💡Parabolic Path
💡Initial Velocity
💡Trigonometry
💡Equations of Motion
💡Free Fall Motion
💡Maximum Height
💡Horizontal Motion
💡Vertical Motion
Highlights
Projectile motion is fundamentally based on the same equations as other types of motion, with the addition of considering both X and Y directions.
The curved path of projectile motion can be broken down into two separate motions: horizontal and vertical.
In projectile motion, the horizontal motion is unaffected by gravity, as gravity only acts in the vertical direction.
The vertical motion in projectile motion is influenced by gravity, with an acceleration of -9.8 m/s^2, directed downward.
The initial velocity of a projectile can be decomposed into horizontal (Vx) and vertical (Vy) components using trigonometric functions (cosine and sine).
The horizontal component of projectile motion maintains a constant velocity since there is no acceleration in the horizontal direction.
The vertical component of projectile motion follows the equations of motion with an acceleration term that accounts for gravity.
The equations of motion for projectile motion in the X and Y directions can be derived from the basic one-dimensional motion equations by considering the absence of acceleration in the X direction and the gravitational acceleration in the Y direction.
In a projectile motion scenario, the object's path is parabolic, which is a result of the combination of the horizontal and vertical motions.
The study of parabolic paths in algebra is directly applicable to understanding the motion of objects in a gravitational field, such as the path traced by a thrown object.
The maximum height and horizontal distance traveled by a projectile can be calculated using the principles of projectile motion.
The hang time, or the time an object remains in the air during projectile motion, can be determined using the equations of motion for the vertical component.
The independence of the horizontal and vertical components of motion means that the horizontal motion is not influenced by the vertical acceleration due to gravity.
An experiment demonstrating the simultaneous impact of two objects, one thrown horizontally and one dropped vertically, illustrates the independence of horizontal and vertical motions in projectile motion.
The vector nature of velocity allows it to be broken down into components along the X and Y axes, which is crucial for analyzing projectile motion.
The concept of breaking down curved motion into horizontal and vertical components is key to solving problems in projectile motion.
Transcripts
Browse More Related Video

Equations of Projectile Motion in Physics Explained - [1-4-6]

AP Physics - Projectile Motion

Solving Projectile Motion Problems in Physics - [1-4-7]

College Physics 1: Lecture 12 - Projectile Motion
Physics 3: Motion in 2-D Projectile Motion (1 of 21) Independent Motion in x and y
introduction to projectile motion
5.0 / 5 (0 votes)
Thanks for rating: