Parabolic Motion
TLDRIn this engaging lecture, Professor Anderson delves into the intricacies of parabolic motion, specifically horizontal projectile motion. By examining motion diagrams and kinematic equations, he clarifies the relationship between the object's height (Y) and time (T), and its horizontal position (X) and time. The professor demonstrates that despite the different representations, both Y vs. X and Y vs. T describe parabolic trajectories. He then presents a remarkable equation that allows for the determination of the object's height at any horizontal position without the need for time, which is particularly useful in horizontal projectile scenarios.
Takeaways
- 📚 The discussion focuses on parabolic motion, specifically the trajectory of an object thrown horizontally from a building.
- 🏋️♂️ The motion diagram typically shows Y as a function of time, but the parabolic shape can also be represented by Y as a function of X.
- 📈 The kinematic equation for displacement in the Y direction is given by y = (Vy_initial^2 - 2g(Y_initial - y)) / (2g), which is a parabolic equation.
- 🔄 The equation has a negative sign because it represents an inverted parabola, starting at height H and moving downwards.
- 🤔 The confusion between Y vs. X and Y vs. time is clarified by showing that both can represent parabolic motion, just in different contexts.
- 📊 The X as a function of time is derived from the kinematic equation X = X_initial + Vx_initial * T + 1/2 a_x * T^2, with initial horizontal velocity Vx_initial being 0.
- 🔗 The relationship between X and T is linear, which helps confirm that the shape of the trajectory is indeed parabolic.
- 🌟 A key insight is that the final equation for Y does not contain time (T), allowing the height at any horizontal position to be determined without knowing the time of flight.
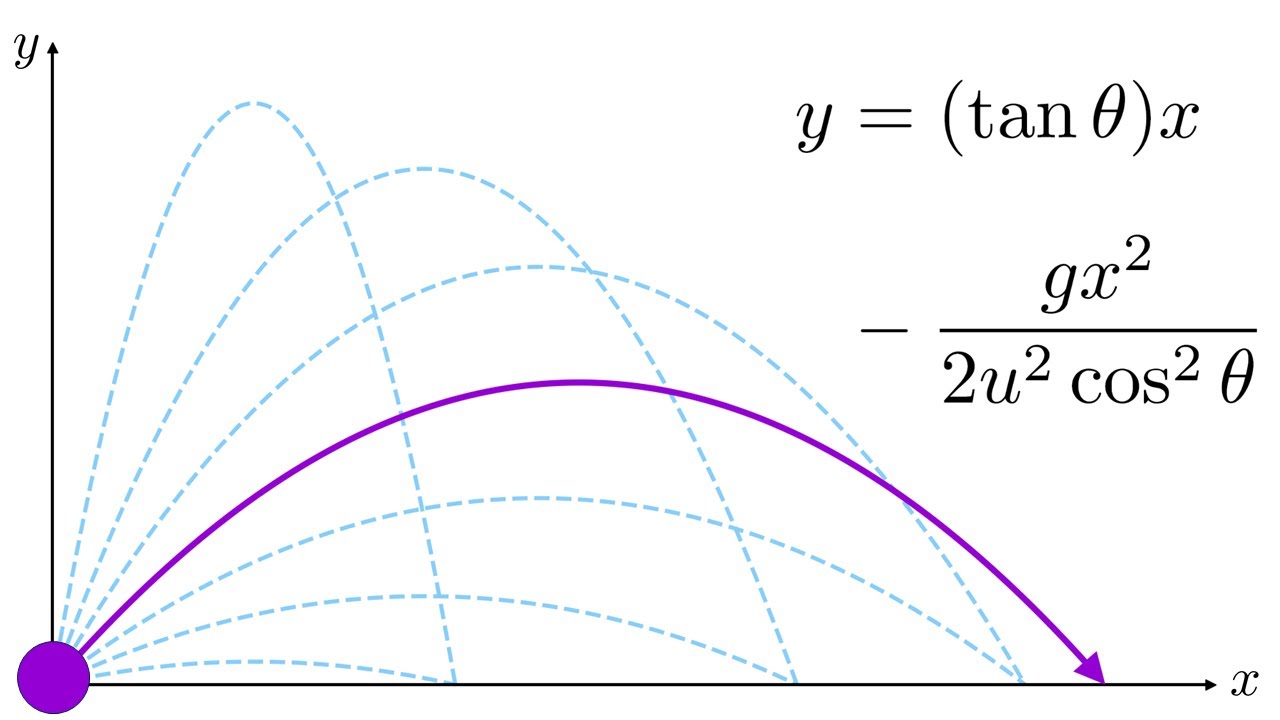
- 🛫 The method can be applied to projectile motion launched at any angle, not just horizontally.
- 📝 The script serves as a lesson on the application of kinematic equations to understand and predict the path of projectiles in motion.
Q & A
What is parabolic motion?
-Parabolic motion refers to the curved path that an object follows when thrown or launched in a particular manner, such as horizontally from a height, under the influence of gravity alone.
How does the shape of a parabola relate to the motion of an object thrown horizontally from a building?
-When an object is thrown horizontally from the top of a building, it follows a parabolic trajectory because the combination of its initial horizontal velocity and the acceleration due to gravity creates a curved path that matches the equation of a parabola.
What are the axes in a motion diagram for parabolic motion?
-In a motion diagram for parabolic motion, the vertical axis (Y-axis) represents the height or position in the air, while the horizontal axis (X-axis) typically represents time or distance traveled horizontally.
Why does the Y as a function of time graph look different from the Y versus X graph for parabolic motion?
-The Y as a function of time graph looks different because it represents the height of the object changing over time, which is an inverted parabola due to the negative acceleration of gravity. In contrast, Y versus X represents the horizontal distance versus height, which is a direct parabola.
What is the kinematic equation used to describe the vertical position of an object in parabolic motion?
-The kinematic equation used to describe the vertical position (Y) of an object in parabolic motion is given by: Y = Y_initial + VY_initial * T + (1/2) * aY * T^2, where Y_initial is the initial height, VY_initial is the initial vertical velocity (which is zero for horizontal throws), T is the time, and aY is the acceleration due to gravity (negative value).
How does the horizontal position of the object (X) change as a function of time?
-The horizontal position (X) changes as a function of time according to the equation: X = X_initial + VX_initial * T, where X_initial is the initial horizontal position (zero at the starting point), VX_initial is the initial horizontal velocity, and T is the time elapsed.
What is the significance of the absence of time (T) in the final equation derived for parabolic motion?
-The absence of time (T) in the final equation signifies that the height of the object (Y) can be determined directly from the horizontal position (X) without needing to know the time of flight. This is particularly useful for solving problems where the time is not given or known.
How does the horizontal velocity (VX_initial) affect the shape of the parabolic trajectory?
-The horizontal velocity (VX_initial) does not affect the shape of the parabola, as the parabolic curve is determined solely by the acceleration due to gravity and the initial height. However, it does affect the horizontal distance the object travels and the overall size of the trajectory.
What happens to the parabolic trajectory if the object is not thrown horizontally but at an angle?
-If the object is thrown at an angle, the trajectory becomes a combination of both horizontal and vertical motion, resulting in a different parabolic equation that still relates Y to X but includes the horizontal and vertical components of the initial velocity and the angle of projection.
Why is it important to understand the relationship between X and T in parabolic motion?
-Understanding the relationship between X and T is important because it allows us to predict the position of the object at any given time during its flight, which is crucial for applications such as sports, engineering, and physics problem-solving.
How does the concept of parabolic motion apply to real-world scenarios outside of the classroom?
-Parabolic motion is a fundamental concept in physics that has practical applications in various fields, including sports (e.g., throwing a ball), engineering (e.g., designing trajectories for projectiles), and space exploration (e.g., calculating trajectories for spacecraft).
Outlines
📚 Introduction to Parabolic Motion
Professor Anderson begins the lecture by discussing parabolic motion, specifically focusing on the trajectory of an object thrown horizontally from the top of a building. The discussion revolves around the shape of the object's path, which follows a parabolic curve before it hits the ground. The professor then delves into motion diagrams, contrasting the typical representation of Y as a function of X (yielding a parabolic curve) with the new scenario where Y is mapped against time. The key point is to understand whether the Y vs. time graph also forms a parabola, which it does, as explained through the kinematic equations involving time (T) and initial vertical velocity (Vy_initial).
📈 Mapping X and Y Functions of Time
This paragraph continues the exploration of parabolic motion by examining the relationship between X and Y as functions of time. The professor clarifies the linear relationship between time (T) and horizontal distance (X), emphasizing that doubling the time results in doubling the horizontal distance. Using kinematic equations, the professor rewrites the Y equation in terms of X, eliminating the need for time (T). This new equation clearly demonstrates that Y is proportional to the square of X, confirming that the trajectory is indeed a parabola. The significance of this finding is that it allows for the determination of the object's height at any horizontal position without knowing the time of flight, which is particularly useful in projectile motion scenarios.
Mindmap
Keywords
💡Parabolic Motion
💡Motion Diagrams
💡Kinematic Equations
💡Y as a Function of Time
💡Projectile Motion
💡X as a Function of Time
💡Acceleration due to Gravity
💡Linear Relationship
💡Equation of a Parabola
💡Office Hours
Highlights
Professor Anderson discusses parabolic motion in detail.
The scenario involves throwing an object horizontally off the top of a building, resulting in parabolic motion.
Motion diagrams are used to illustrate the relationship between position and time.
The kinematic equation for vertical displacement is derived and connected to the parabolic shape.
The equation for vertical displacement (y) as a function of time is shown to be parabolic due to the presence of t^2.
The relationship between y versus x and y as a function of time is clarified, both resulting in parabolic motion.
The horizontal displacement (x) as a function of time is explored and found to be linear, not parabolic.
The linear relationship between time (T) and horizontal displacement (X) is established.
A new equation for y in terms of x is derived, eliminating the need for time (T).
The derived equation demonstrates that the height of the projectile can be determined at any horizontal position without knowing the time.
The significance of the derived equation is that it simplifies the process of finding the projectile's height at any given horizontal distance.
The method is applicable specifically for horizontal launches but can be generalized for other angles.
The discussion emphasizes the importance of understanding the relationship between variables in parabolic motion.
The practical application of the equations allows for predicting the trajectory of projectiles in real-world scenarios.
The session concludes with an invitation for further clarification during office hours.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: