How to find Area of a Velocity vs Time Graph
TLDRThe video explores the historical significance of velocity versus time graphs, highlighting Aristotle's qualitative view of the world and the limitations it imposed on quantifying motion. It then delves into Nicole Orisma's revolutionary approach with the Oxford Calculators, who challenged Aristotle's teachings by introducing the concept that the area under a velocity-time graph represents displacement. The video uses the example of a car speeding and a police officer catching up to illustrate this concept. It also touches on Galileo's experiments that confirmed the reality of accelerated motion and its measurability. The video concludes with practical applications of these concepts in solving physics problems, emphasizing the importance of understanding displacement and distance through velocity-time graphs.
Takeaways
- 📚 The concept of using the area under a velocity vs. time graph to represent displacement was first explored by scholars challenging Aristotle's qualitative view of the world.
- 🎓 Aristotle's teachings dominated academic thought in the Middle Ages, asserting that the world was qualitative and could not be quantified, including concepts like speed and acceleration.
- 🌐 The Oxford Calculators, including Nicole Orisma, were a group of mathematician-philosophers who contributed to the early development of mathematical concepts like the mean speed theorem.
- 🚗 Nicole Orisma used the idea of areas in velocity vs. time graphs to solve the mean speed theorem, which states that the areas under the graphs represent distances traveled.
- 📈 The mean speed theorem was applied to a hypothetical scenario where a car is traveling at a constant speed and a police officer is accelerating to catch up, demonstrating that the officer must travel at twice the speed to catch the car.
- 🛤️ The area under a velocity vs. time graph represents displacement, which is the change in position, not the absolute position.
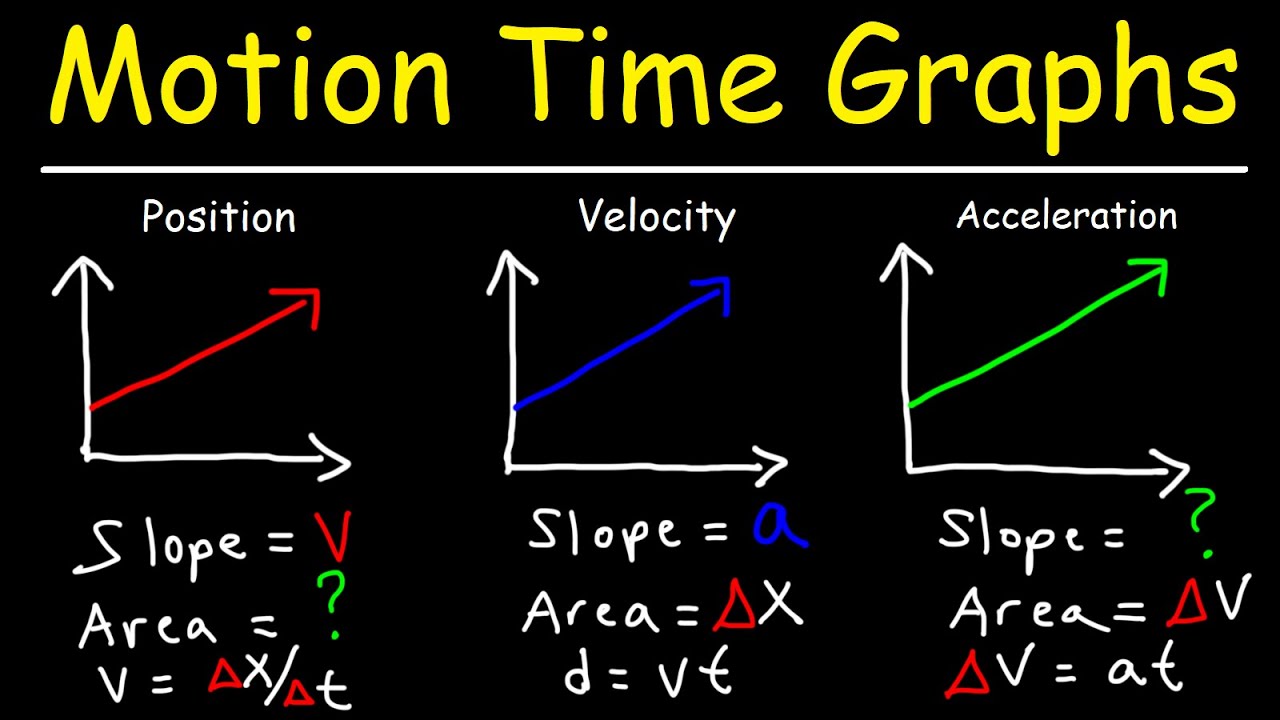
- 📊 The slope of a velocity vs. time graph represents acceleration, calculated as the change in velocity over the change in time.
- 🎯 To find displacement using a velocity vs. time graph, one can break the graph into geometric shapes (rectangles and triangles) and calculate the areas to determine the total displacement.
- 🔄 The concept of acceleration was experimentally validated by Galileo, who showed that objects rolling down an inclined plane accelerated and that this acceleration could be measured.
- 🔢 The historical development of these mathematical concepts illustrates the transition from qualitative to quantitative understanding of motion and the physical world.
- 💡 Understanding velocity vs. time graphs and their areas is crucial for analyzing motion and solving physics problems related to displacement and distance traveled.
Q & A
What is the significance of the area under a velocity versus time graph?
-The area under a velocity versus time graph represents the displacement of an object. It indicates the total change in position over the time period depicted in the graph.
Who was the first person to associate the area of a graph with a physical quantity?
-Nicole Orisma, a member of the Oxford Calculators, was the first to associate the area under a velocity versus time graph with displacement, as part of solving the mean speed theorem.
What was Aristotle's view on the quantifiability of the world?
-Aristotle believed that the world was qualitative, not quantifiable. He argued that trying to quantify the world led to confusion and that concepts like speed could not be accurately measured.
How did the Scholastics interpret Aristotle's teachings on speed and motion?
-The Scholastics, who were the teachers of Aristotle's works, interpreted his teachings to mean that speed could not be quantified. Some even argued that speeding up and slowing down were impossible or nonsensical concepts.
What did Nicole Orisma contribute to the understanding of motion?
-Nicole Orisma contributed to the understanding of motion by proposing a method to solve the mean speed theorem. He demonstrated that the area under a velocity versus time graph could be used to calculate displacement, which was a significant step towards quantifying motion.
What is the mean speed theorem and how did Nicole Orisma solve it?
-The mean speed theorem is a problem in mathematics that involves determining the speed required for an object to cover a certain distance in the same time as another object moving at a constant speed. Nicole Orisma solved it by using the area under a velocity versus time graph to represent displacement, and showing that the area of a triangle with a height twice that of the initial speed's rectangle would be equal to the area of the rectangle, indicating the cop's speed was twice that of the constant speed.
How did Galileo of Galilee build upon Nicole Orisma's work on motion?
-Galileo of Galilee built upon Nicole Orisma's work by providing empirical evidence for accelerated motion. He used a wooden ramp with bells to measure the distances covered by balls at equal time intervals, demonstrating that objects accelerate and that this acceleration can be quantitatively measured.
What is the difference between displacement and distance in the context of motion?
-Displacement refers to the change in position of an object and has both magnitude and direction, while distance is the total length of the path traveled by the object, regardless of direction. Displacement can be positive or negative depending on the direction of movement, whereas distance is always positive.
How can you calculate the displacement from a velocity versus time graph?
-To calculate the displacement from a velocity versus time graph, you can divide the graph into shapes (like rectangles or triangles) and calculate the area of each shape. The total area of these shapes represents the total displacement.
How can you find the distance traveled from a velocity versus time graph?
-To find the distance traveled from a velocity versus time graph, you sum the areas of the shapes under the graph without considering their sign (positive or negative). This gives you the total distance, which is the absolute value of the path taken.
What is the historical significance of the transition from Aristotelian to quantifiable views of motion?
-The transition from Aristotelian qualitative views of motion to quantifiable views marked a significant shift in scientific thinking. It allowed for the development of modern physics, where motion and other natural phenomena could be described and predicted using mathematical models, leading to a greater understanding and control over the natural world.
Outlines
📚 Historical Context of Velocity vs. Time Graphs
This paragraph delves into the historical significance of velocity versus time graphs, highlighting the academic 'powers that be' and their influence on the development of these concepts. Aristotle's qualitative view of the world and the limitations it imposed on quantifying speed and motion are discussed. The paragraph then transitions to the Renaissance period, where thinkers like Nicole Orisma challenged Aristotle's teachings, leading to the exploration of quantifiable aspects of motion. The introduction of the concept that the area under a velocity-time graph represents displacement is attributed to Orisma, who was part of the Oxford Calculators group.
🔍 Solving the Mean Speed Theorem with Velocity-Time Graphs
The second paragraph focuses on the practical application of velocity-time graphs to solve the mean speed theorem, a mathematical riddle. It describes how Nicole Orisma used the area under a velocity-time graph to represent distance traveled. The paragraph outlines the steps Orisma took to solve the riddle, which involved comparing the areas of a rectangle and a triangle to determine the speed at which a police officer would catch up to a speeding driver. The explanation includes the mathematical reasoning behind the solution and touches on the historical context of how this theorem was a significant departure from the Aristotelian view of the world.
📈 Applying the Concept to Practice Problems
This paragraph shifts the focus to practical problem-solving using velocity-time graphs. It provides a step-by-step guide on how to graph and calculate displacement using the area under the velocity-time graph for a given scenario. The example involves Marty McFly accelerating at a constant rate and uses the slope of the velocity-time graph to determine the change in velocity. The paragraph emphasizes the importance of understanding that the area under the graph represents displacement, not the final position, and how this concept can be applied to solve real-world physics problems.
🌟 Further Exploration of Displacement and Distance
The final paragraph continues the exploration of velocity-time graphs by differentiating between displacement and distance. It explains how the area above and below the time axis represents positive and negative displacements, respectively, while distance is the total magnitude of the movement without considering direction. The paragraph presents a problem that requires calculating both displacement and distance from a given graph, illustrating how to determine these values by counting 'boxes' under the curve and adding their magnitudes. The summary concludes by congratulating the viewer on their understanding of both the mathematical concepts and the historical philosophies that underpin the study of motion.
Mindmap
Keywords
💡Aristotle
💡Scholasticism
💡Quantification
💡Nicole Orisma
💡Mean Speed Theorem
💡Displacement
💡Acceleration
💡Velocity-Time Graph
💡Renaissance
💡Galileo Galilei
💡Oxford Calculators
Highlights
The concept of using the area of a graph to represent meaningful values was first explored in the context of a velocity versus time graph.
Aristotle's teachings dominated academic thought for over a thousand years, emphasizing a qualitative view of the world rather than a quantitative one.
The Scholastics, who taught Aristotle's works, believed that quantifying concepts like speed led to confusion and thus avoided mathematical approaches to such topics.
The idea that the world was not quantifiable was challenged during the Renaissance, leading to new perspectives on the nature of reality.
Nicole Orisma, a member of the Oxford Calculators, proposed a method to solve the mean speed theorem, which was akin to a math riddle.
Orisma used the concept of the area of shapes to represent distance traveled, which was a revolutionary approach to understanding velocity and time relationships.
The area under a velocity versus time graph represents displacement, a key concept in understanding changes in position.
The historical context of the academic world's shift from qualitative to quantitative understanding is highlighted through the work of figures like Orisma and the challenges to Aristotelian thought.
Galileo of Galilee later confirmed the reality of accelerated motion and the possibility of quantifying it, building on the theoretical work of predecessors like Orisma.
The practical application of velocity versus time graphs allows for the calculation of displacement and distance traveled over time.
The method of breaking down a graph into shapes to calculate areas represents a fundamental approach to understanding the relationship between velocity, time, and displacement.
The importance of distinguishing between displacement (change in position) and distance (total path traveled) is clarified through the analysis of velocity versus time graphs.
The historical progression from Aristotelian qualitative views to the quantitative methods of the Renaissance mathematicians underscores the evolving nature of scientific understanding.
The use of velocity versus time graphs not only illustrates the relationship between velocity and time but also provides a visual method for solving complex motion problems.
The video's exploration of the history and development of velocity versus time graphs offers a comprehensive understanding of the subject, from theoretical origins to practical applications.
The mean speed theorem, as proposed by Orisma, demonstrates that the area of a triangle with twice the height of a given rectangle can represent the same displacement, leading to insights about relative speeds.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: