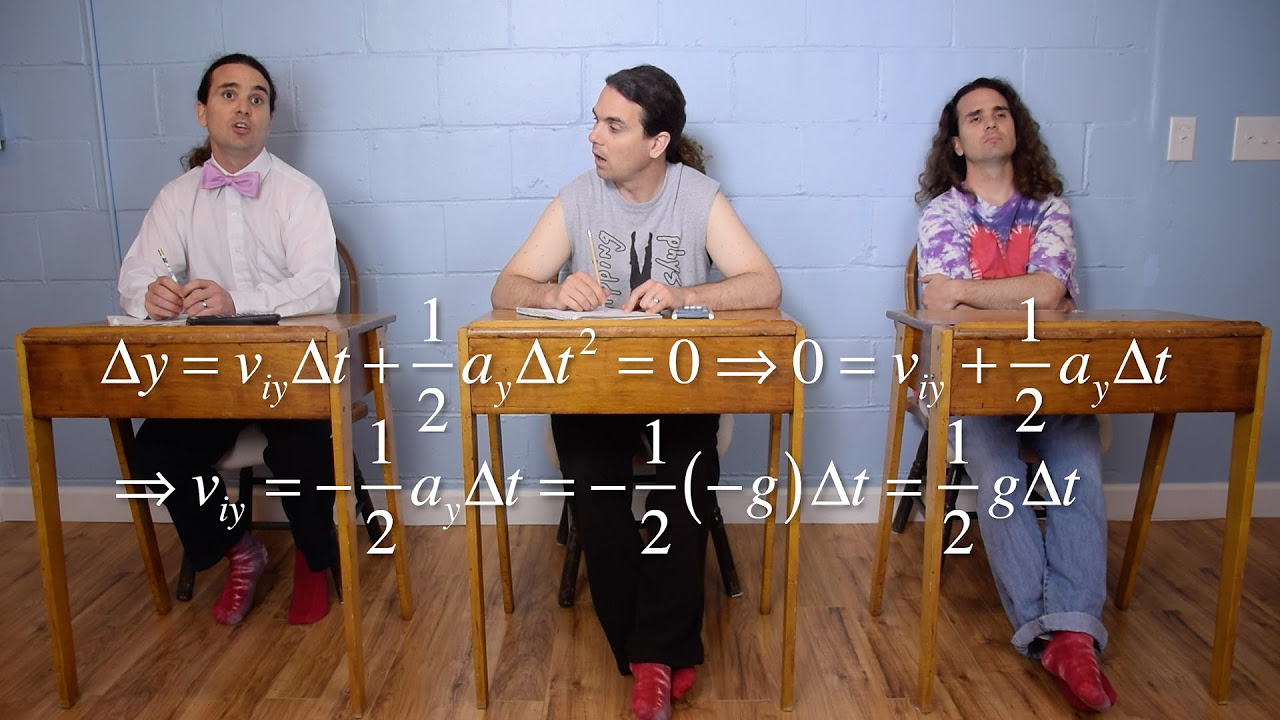8.01x - Lect 4 - 3D Kinematics, Free Falling Reference Frames
TLDRIn this engaging lecture, the professor explores the physics of projectile motion, using golf and tennis balls to demonstrate concepts such as trajectory, velocity components, and the influence of gravity. The discussion delves into the equations of motion, highlighting the parabolic path of projectiles and the critical role of initial velocity and angle. The lecture also includes a dramatic demonstration involving a 'monkey' and a golf ball, illustrating the impact of gravity on projectile paths and the importance of precise aiming. The content is both educational and entertaining, with a touch of humor and a strong emphasis on the practical application of theoretical physics.
Takeaways
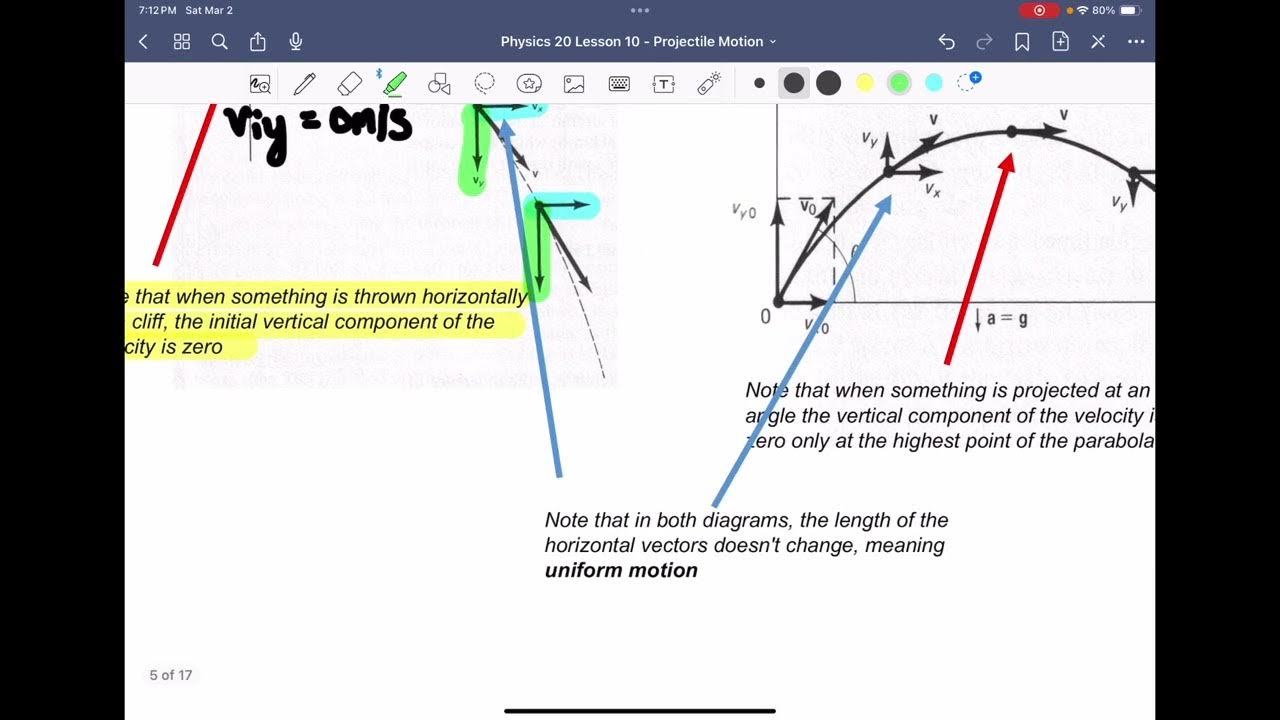
- 🎾 The trajectory of a golf ball or tennis ball can be described using the principles of projectile motion, with its path shaped by the components of velocity in the horizontal (x) and vertical (y) directions.
- 📈 The shape of the projectile motion is a parabola, which is a second-order equation in x and is derived by eliminating the time variable from the equations of motion.
- 🕒 The time it takes for the projectile to reach its highest point is determined by the vertical component of the initial velocity and the acceleration due to gravity.
- 📍 The highest point reached by the projectile in the y direction is directly proportional to the square of the initial velocity (v_zero) and depends on the angle (alpha) at which it is projected.
- 🚀 The horizontal component of the velocity remains constant throughout the motion, while the vertical component changes due to the acceleration of gravity.
- 🕒 The total time for the projectile to return to the ground is twice the time it takes to reach the highest point, due to the symmetry of the parabolic trajectory.
- 📊 The distance traveled by the projectile (OS) can be calculated using the horizontal component of the initial velocity and the time of flight.
- 🌕 Experiments on the moon would result in a higher trajectory for the same initial speed due to the lower gravitational acceleration.
- 🔬 Accurate measurements and consideration of uncertainties are crucial in experiments involving projectile motion, as small errors can lead to significant discrepancies in predicted outcomes.
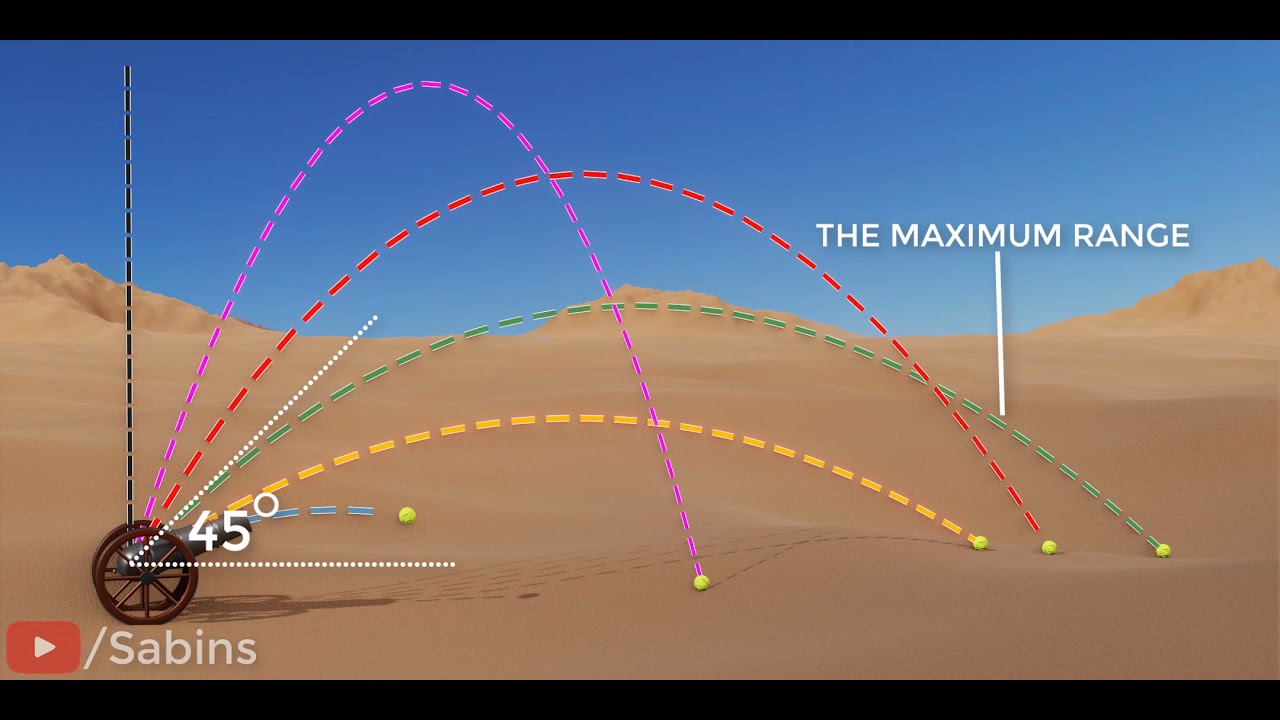
- 🎯 The angle of projection plays a critical role in determining the range and height of the projectile, with the maximum range achieved at an angle of 45 degrees.
- 🦍 A hypothetical scenario involving a monkey and a golf ball gun illustrates the application of projectile motion concepts and the importance of understanding the relative motion from different reference frames.
Q & A
What is the main topic of the lecture?
-The main topic of the lecture is the application of physics principles to the trajectory of a golf ball or a tennis ball, focusing on its motion, highest point, and the distance it travels.
How does the讲师 describe the initial velocity components of the ball?
-The讲师 describes the initial velocity components as v_zero cosine alpha for the horizontal component in the x direction and v_zero sine alpha for the vertical component in the y direction.
What is the significance of the point P in the trajectory?
-Point P represents the highest point the ball reaches in its trajectory before it begins to descend back to the ground.
How does the讲师 determine the time it takes for the ball to reach the highest point?
-The讲师 determines the time it takes for the ball to reach the highest point by setting the velocity in the y direction to zero and solving the equation v_zero sine alpha - gt = 0 for t, resulting in t = v_zero sine alpha / g.
What is the equation for the shape of the ball's trajectory?
-The equation for the shape of the ball's trajectory is y = (v_zero sine alpha) * t - (1/2) * g * t^2, which simplifies to a parabolic equation in x, y = (tan(alpha)) * x - (1/2) * g * x^2, indicating a parabola.
How does the讲师 explain the relationship between the initial velocity (v_zero) and the maximum height reached by the ball?
-The讲师 explains that the maximum height reached by the ball is directly proportional to the square of the initial velocity (v_zero squared), as seen in the equation h = (v_zero^2 * sine alpha^2) / (2 * g).
What is the significance of the angle alpha in the trajectory analysis?
-The angle alpha is significant because it affects the direction and height of the ball's trajectory. The讲师 demonstrates that the highest point reached by the ball in the sky increases with larger angles, up to 90 degrees, where the trajectory becomes vertical.
How does the讲师 approach the experimental verification of the theoretical predictions?
-The讲师 uses a spring gun to launch a metal ball at various angles and measures the actual height and distance traveled to verify the theoretical predictions. The讲师 also considers the uncertainties in the measurements and the potential variations in the ball's velocity.
What is the purpose of the monkey demonstration in the lecture?
-The purpose of the monkey demonstration is to illustrate the practical application of the physics concepts discussed in the lecture, specifically the impact of gravity on the trajectory of a projectile and the importance of accurate aiming.
How does the lecturer incorporate humor into the lecture?
-The lecturer incorporates humor by using a stuffed monkey named Robert as a prop in the demonstration, creating a playful and engaging scenario that makes the physics concepts more relatable and memorable for the audience.
What is the significance of the equation for the distance traveled by the ball (OS)?
-The equation for the distance traveled by the ball (OS) is significant because it allows the lecturer to make predictions about where the ball will land at different angles and initial velocities. It also demonstrates the importance of understanding the relationship between the physical quantities involved in the motion of the ball.
Outlines
📚 Introduction to Trajectory Analysis
The speaker begins by stating that the session will be a review of previously learned material, focusing on the application of knowledge rather than introducing new concepts. The discussion revolves around the trajectory of a golf or tennis ball, its components in the x and y directions, and the equations that describe its motion. The speaker emphasizes the importance of understanding these equations and their practical applications, particularly in relation to the constant values used in the calculations.
🕒 Time and Velocity at the Highest Point
The speaker delves into the specifics of when and where the ball reaches its highest point in the trajectory. By analyzing the velocity equations, the speaker determines the time it takes for the ball to reach the highest point and the height of this point above the ground. The discussion highlights how varying initial conditions, such as speed and angle of projection, affect the maximum height. The speaker also touches on the intuitive understanding of these effects and the influence of gravitational acceleration (g) on the trajectory.
🚀 Understanding the Trajectory Shape and Distance Traveled
The speaker explains the shape of the projectile's trajectory, which is a parabola, and further explores the time and distance aspects of the motion. The analysis includes the time it takes for the ball to reach the ground after being launched and the total distance traveled during the flight. The speaker also discusses the implications of changing the initial speed and angle, and how these changes would affect the trajectory's characteristics. The segment concludes with a thought experiment about the distance traveled, emphasizing the quadratic relationship with the initial speed (v zero squared).
🎯 Predicting Impact Points and Uncertainties
The speaker engages in an experimental approach to test the theoretical predictions made earlier. By firing a pellet at different angles, the speaker attempts to predict where it will land on a table and acknowledges the inherent uncertainties in the measurements. The process involves calculating the velocity of the pellet and understanding the variability in the outcomes. The speaker emphasizes the importance of accounting for these uncertainties in real-world applications and uses an interactive approach to involve the audience in the measurements and predictions.
🌟 The 45-Degree Optimal Angle for Maximum Distance
The speaker focuses on the optimal angle for achieving maximum distance in a projectile motion, which is 45 degrees. The explanation includes a detailed calculation of the expected distance traveled by the projectile when launched at this angle, taking into account the previously measured velocity and the effects of air resistance. The speaker also discusses the practical implications of the calculations and how they relate to real-world scenarios, such as sports, and the importance of understanding and accounting for uncertainties in these calculations.
📐 Predicting Trajectory at 30 Degrees
The speaker continues the experimental analysis by predicting the projectile's trajectory at a 30-degree angle. The discussion includes the calculation of the expected impact point, considering the uncertainties in the angle and the initial velocity squared. The speaker highlights the increased uncertainty due to the sine of the angle and the potential for a larger error in the prediction. The segment also involves a live demonstration of the projectile's trajectory, emphasizing the need for precise measurements and the impact of small errors on the outcome.
🐒 The Tragic Monkey and Projectile Motion
The speaker introduces a hypothetical scenario involving a monkey and a hunter to illustrate the principles of projectile motion. The scenario involves calculating the monkey's safety based on the trajectory of a golf ball fired by the hunter. The speaker explains how the presence of gravity affects the projectile's path and how the monkey's reaction to the gunshot determines its fate. The segment aims to engage the audience with a dramatic narrative while reinforcing the concepts of projectile motion and the importance of understanding the effects of gravity.
🤔 Perspective of the Monkey and Free Fall
The speaker explores the perspective of the monkey in the previous scenario, considering it as being in a free-falling elevator. This thought experiment aims to demonstrate that the time until impact is consistent regardless of the reference frame. The speaker explains how the monkey would calculate its remaining time based on the distance and height, and how this calculation aligns with the predictions made from a stationary reference frame. The segment emphasizes the universality of physical laws and the importance of understanding different perspectives in analyzing motion.
🎭 Dramatic Demonstration with Robert the Monkey
The speaker sets up a dramatic demonstration involving a monkey named Robert, placed at a height to mimic the trajectory of a golf ball. The intention is to visually represent the theoretical concepts discussed earlier. The speaker uses humor and audience interaction to lighten the mood, while also ensuring that safety measures, such as a bulletproof vest for Robert, are in place. The segment concludes with the speaker preparing to conduct the demonstration, creating anticipation for the outcome.
Mindmap
Keywords
💡Trajectory
💡Velocity Components
💡Acceleration
💡Highest Point
💡Parabola
💡Time of Flight
💡Projectile Motion
💡Equations of Motion
💡Free Fall
💡Critical Angle
💡Uncertainty
Highlights
The lecture begins with an emphasis on applying previously learned concepts, focusing on their practical applications rather than introducing new material.
A trajectory of a golf ball or tennis ball is discussed, using the example to illustrate the principles of motion in two dimensions.
The horizontal and vertical components of the ball's velocity are described using trigonometric functions, with the horizontal component being constant and the vertical component changing due to acceleration caused by gravity.
The equations for motion in the x and y directions are used to analyze the ball's path, highlighting the importance of understanding these equations for practical applications.
The shape of the ball's trajectory is determined to be a parabola, derived by eliminating the time variable from the equations of motion.
The time it takes for the ball to reach its highest point is calculated using the equations of motion, providing insight into the relationship between velocity, angle, and time.
The highest point of the ball's trajectory is found to be dependent on the initial velocity and the angle of projection, with a formula provided for calculating this maximum height.
The time it takes for the ball to return to the ground is twice the time it takes to reach the highest point, due to the symmetry of the parabolic trajectory.
The total distance traveled by the ball (OS) is calculated using the derived equations, with the result depending on the initial velocity and the angle of projection.
The lecture includes a discussion on the importance of considering uncertainties in measurements, with an example provided on how to estimate and incorporate these uncertainties.
An experimental demonstration is conducted to test the theoretical predictions, involving shooting a pellet at various angles and measuring the resulting heights and distances.
The results of the experiment are used to validate the derived equations and to demonstrate the impact of initial conditions on the outcome of projectile motion.
The lecture concludes with a dramatic demonstration involving a 'monkey' in a tree, illustrating the tragic consequences of not understanding the principles of projectile motion.
The 'monkey' demonstration emphasizes the practical implications of physics and the importance of accurate calculations in real-world scenarios.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: