Projectile Motion Example - How fast when it hits the ground

Physics with Professor Matt Anderson
9 Oct 201411:35
EducationalLearning
32 Likes 10 Comments

TLDRIn this engaging physics lesson, Professor Anderson tackles a projectile motion problem, launching an object from a building at an angle. Given initial velocity (20 m/s), angle (30 degrees), and height (45 meters), the professor guides students through the calculations to find the object's final speed and time in the air. The surprising result: the final speed before impact is independent of the angle of projection, a counterintuitive insight drawn from the kinematic equations.

Takeaways
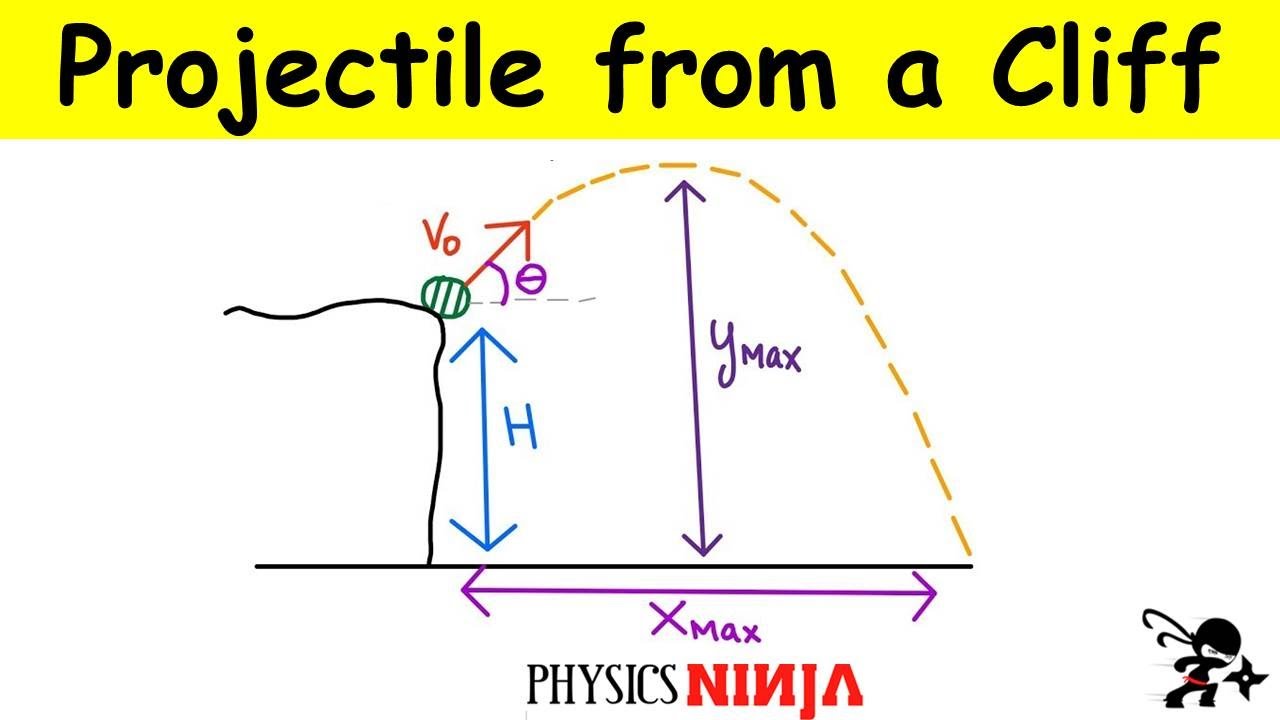
  • 📚 The lecture introduces a projectile motion problem involving launching an object from the top of a building at an angle above the horizontal.
  • 🎯 The initial conditions given are an initial velocity (VI) of 20 m/s, an angle (theta) of 30 degrees, and an initial height (H) of 45 meters.
  • 🚀 The object follows a parabolic curve due to projectile motion, and its horizontal velocity component remains constant throughout the motion.
  • 📐 For the vertical component, the acceleration is equal to the gravitational acceleration (-9.8 m/s²), which affects the final vertical velocity.
  • 🔢 The final speed (VF) can be calculated using the equation VF = √(VI² + 2GH), which is independent of the angle of projection.
  • 🌐 The final speed is found to be approximately 42.21 m/s when plugging in the given values, showcasing the counterintuitive nature of projectile motion.
  • 🤔 The angle of projection does not affect the final speed when the object returns to the same height from which it was launched, ignoring air resistance.
  • 🛑 The final velocity's direction changes depending on the angle of projection, but the speed remains the same regardless of the direction.
  • 📉 The vertical displacement (YF - YI) is used in the kinematic equation to calculate the final vertical velocity component.
  • 🕒 The time the object is in the air is not directly addressed in the provided script excerpt, but it could be calculated using additional kinematic equations.
  • 📌 The script emphasizes the importance of understanding the independence of the final speed from the angle of projection in the context of projectile motion.
Q & A

  • What is the context of the discussion in the transcript?

    -The transcript is from a lecture on physics, specifically focusing on a projectile motion problem involving an object launched from the top of a building at an angle.

  • What is the significance of the angle theta in the problem?

    -The angle theta represents the angle at which the object is launched from the building. However, it is noted that the final speed of the projectile upon hitting the ground is independent of this angle, which might seem counterintuitive.

  • What are the given parameters for the projectile motion problem?

    -The given parameters are an initial velocity (VI) of 20 meters per second, an angle (theta) of 30 degrees, and an initial height (H) of 45 meters.

  • How does the object's motion change in the horizontal and vertical directions?

    -In the horizontal direction, the object's speed (VX) remains constant because there is no acceleration. In the vertical direction, the object's speed (VY) changes due to the acceleration caused by gravity, which is -9.8 m/s^2.

  • What is the final speed of the projectile just before it hits the ground?

    -The final speed of the projectile just before impact is approximately 42.21 meters per second, calculated using the equation VF = sqrt(VI^2 + 2*G*H).

  • Why is the final speed of the projectile independent of the angle at which it was launched?

    -The final speed is independent of the angle because the speed component in the vertical direction (VY) is what changes due to gravity, and when the object returns to the same height (or lower), the vertical speed component is the same as if it was thrown straight up or down.

  • How does the height from which the object is launched affect its final speed?

    -The height (H) affects the final speed because it is part of the equation that calculates the change in vertical speed due to gravity (2*G*H). A greater height results in a greater change in vertical speed, thus affecting the final speed.

  • What is the significance of the kinematic equations in solving this problem?

    -The kinematic equations are crucial for understanding the relationship between initial velocity, acceleration, displacement, and final velocity. They help in breaking down the motion into components and calculating the final velocity of the projectile.

  • What is the role of gravity in the projectile motion?

    -Gravity is the force that causes the object to accelerate downwards, affecting only the vertical component of the motion. It is responsible for the change in the object's vertical speed from its initial value to its final value just before impact.

  • How does the initial velocity's horizontal and vertical components relate to the final velocity?

    -The horizontal component of the initial velocity (VXI) remains unchanged throughout the motion due to the lack of horizontal acceleration. The vertical component (VYI) changes due to gravity. The final velocity (VF) is the vector sum of the unchanged horizontal component and the changed vertical component.

  • What is the significance of the final velocity's direction?

    -While the final speed is independent of the angle of launch, the direction of the final velocity is not. The direction changes based on the angle of launch and affects the trajectory of the projectile, following a parabolic path.

Outlines
00:00
📚 Introduction to Projectile Motion

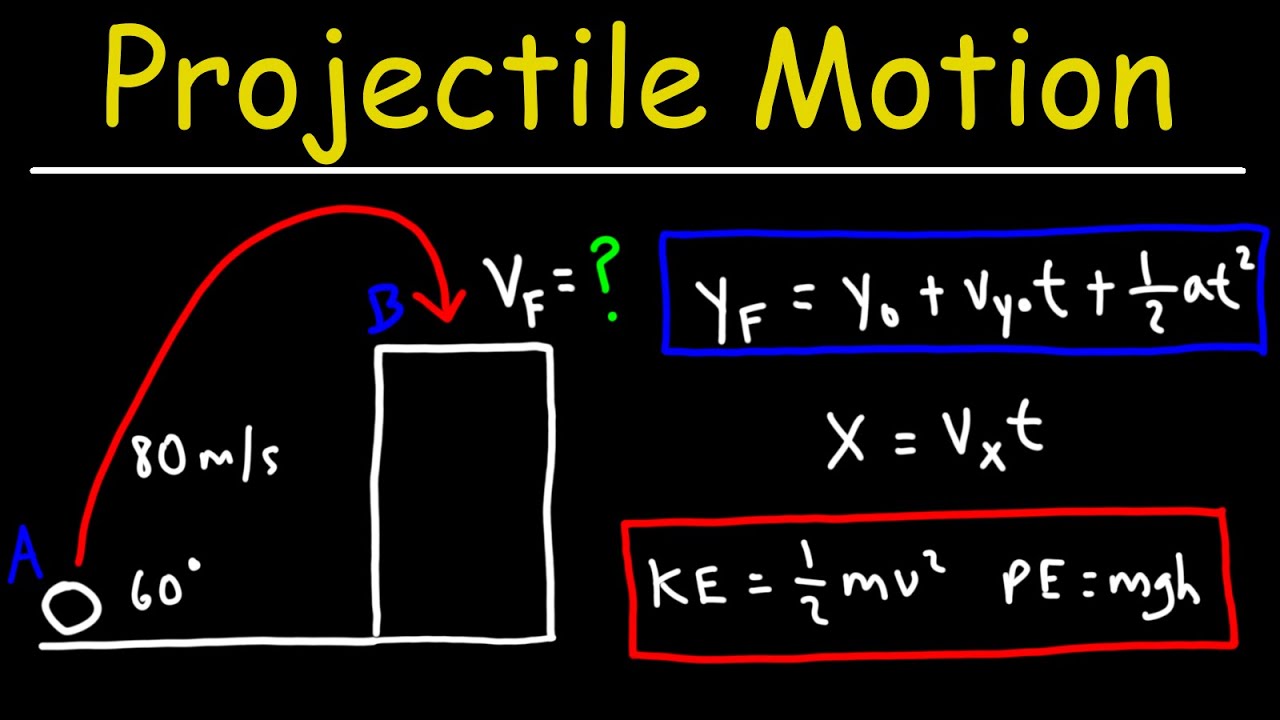
Professor Anderson begins the lesson by discussing projectile motion, using the scenario of launching an object from the top of a building at an angle. The initial conditions given are an initial velocity (VI) of 20 m/s, an angle (theta) of 30 degrees, and an initial height (H) of 45 meters. The professor introduces two questions: how long the object is in the air (Question A) and its final speed (Question B). The approach to solving these questions is discussed, with a focus on the second question first, using kinematic equations and the understanding that the horizontal component of velocity remains constant for a projectile.

05:04
🚀 Calculation of Final Speed

The professor continues the discussion on calculating the final speed of the projectile. Using the kinematic equation for the vertical component of velocity (VY), the professor explains how to find the final vertical velocity (VYF) by considering the acceleration due to gravity (G). The equation VYF squared equals VYI squared minus 2GH is used, with VYI being the initial vertical velocity and H being the initial height. The professor then combines the horizontal and vertical components to find the final speed (VF) using the Pythagorean theorem, resulting in the equation VF equals the square root of VI squared plus 2GH. After plugging in the given values, the professor approximates the final speed to be around 43 m/s, which is then confirmed by a student's calculation of 42.21 m/s.

10:04
🤔 The Intuition Behind Final Speed Calculation

The professor delves into the counterintuitive nature of projectile motion, specifically the fact that the final speed of the projectile is independent of the angle at which it was thrown. This is illustrated by the example of throwing a ball straight up and down from a building, which would result in the same final speed, VI, regardless of the direction. The professor emphasizes that the final speed calculation, square root of VI squared plus 2GH, holds true for any direction the ball is thrown from the building, with the only difference being the direction of the final velocity.

Mindmap
Keywords
💡Projectile Motion
Projectile motion refers to the motion of an object that is launched into the air and moves under the influence of gravity and air resistance. In the video, the professor discusses a specific example of projectile motion where an object is launched from the top of a building at an angle to the horizontal. This concept is central to the problem-solving process as it governs the parabolic trajectory of the object and is used to calculate its final speed and time in the air.
💡Parabolic Curve
A parabolic curve is the path followed by a projectile in motion, which is a 'U' shaped curve. In the context of the video, the object launched from the building follows a parabolic curve due to the influence of gravity acting upon it. The shape of this curve is crucial in understanding the object's trajectory and is integral to solving the physics problem presented.
💡Initial Velocity (VI)
Initial velocity, often denoted as VI, is the speed at which an object begins its motion. In the video, the initial velocity is given as 20 meters per second and is a critical parameter for calculating the object's trajectory and final speed. It is a vector quantity, meaning it has both magnitude and direction, and is essential for applying the equations of motion to projectile problems.
💡Angle (Theta)
The angle, symbolized as theta, is the measure of the inclination of the object's trajectory relative to the horizontal plane. In the video, the angle is set at 30 degrees, indicating that the object is not launched straight up or horizontally but at an intermediate angle. This angle affects the object's trajectory and the components of its initial velocity in the horizontal (X) and vertical (Y) directions.
💡Height (H)
Height (H) refers to the vertical distance from the ground to the starting point of the projectile, which in this case is the top of the building. It is an essential parameter in calculating the object's trajectory and final speed, as it is directly related to the vertical component of the motion and the work done by gravity.
💡Acceleration (A)
Acceleration (A) is the rate of change of velocity with respect to time. In the context of projectile motion, the only acceleration acting on the object (ignoring air resistance) is the acceleration due to gravity, which is constant at approximately 9.8 m/s^2 towards the Earth's surface. This acceleration affects the object's vertical motion, causing it to speed up as it falls and to slow down if it were moving upward.
💡Kinematic Equations
Kinematic equations are mathematical formulas that relate an object's displacement, velocity, acceleration, and time. They are essential tools in physics for analyzing motion. In the video, the professor refers to these equations to solve for the object's final speed and time in the air, specifically using the equations for final velocity in both the horizontal and vertical directions.
💡Final Speed (VF)
Final speed (VF) is the speed of the object at the end of its motion, just before it reaches the ground. It is the resultant of the horizontal and vertical components of velocity. In the video, the professor calculates the final speed by using the given initial conditions and the kinematic equations, which is a critical step in understanding the outcome of the projectile motion.
💡Horizontal Component (VX)
The horizontal component (VX) of an object's velocity is the speed at which it moves along the horizontal axis. In projectile motion, the horizontal component remains constant throughout the motion because there are no forces acting in the horizontal direction (assuming no air resistance). This component is essential for calculating the object's trajectory and total distance traveled.
💡Vertical Component (VY)
The vertical component (VY) of an object's velocity is the speed at which it moves along the vertical axis. In the context of projectile motion, the vertical component changes due to the acceleration caused by gravity. The vertical component is crucial for understanding the object's height change and its time in the air.
💡Pythagorean Theorem
The Pythagorean theorem is a fundamental principle in geometry that states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. In the video, the theorem is implicitly used to relate the horizontal and vertical components of the object's velocity to its overall final velocity.
Highlights

Professor Anderson introduces a projectile motion problem to the class.

The scenario involves launching an object from the top of a building at an angle above the horizontal.

The object's trajectory is described as a parabolic curve.

Initial conditions provided are a height (H) of 45 meters, an initial velocity (VI) of 20 m/s, and an angle (theta) of 30 degrees.

Question A asks for the time the object is in the air, and Question B asks for its final speed.

The professor suggests solving Question B (final speed) first and revisits the kinematic equations.

For a projectile, the horizontal component of velocity (VX) remains constant because the acceleration in the X direction is zero.

The vertical component of velocity (VY) is affected by gravity, with an acceleration of -9.8 m/s^2.

The final vertical velocity (VYF) can be calculated using the equation VYF^2 = VYI^2 - 2GH, where YF is zero and H is the initial height.

The final velocity (VF) is the vector sum of the horizontal and vertical components and can be found using the Pythagorean theorem.

The calculation for VF results in a final speed of approximately 42.21 m/s, derived from the equation √(VI^2 + 2GH).

The professor points out that the final speed is independent of the angle (theta) at which the object was thrown.

An object thrown vertically will have the same final speed upon returning to the thrower's level as its initial speed, ignoring air resistance.

The final speed of a projectile thrown from a building is determined solely by the initial speed and the height from which it is thrown.

The direction of the final velocity changes with the angle of projection, but the speed remains constant for a given initial speed and height.

The professor emphasizes the counterintuitive nature of the projectile's final speed being independent of the angle of projection.

The problem-solving approach involves a combination of kinematic equations and vector addition to find the final speed and time of flight.

The lecture concludes with a confirmation that the final speed calculation does not require the angle of projection, which is a unique insight into projectile motion.

Transcripts

Browse More Related Video

Projectile launched off a cliff at an angle

Projectile Launched of a Cliff

Win the Prize Projectile Motion Problem

Two Dimensional Motion Problems - Physics

Man Throws Rock Projectile Motion Problem

Projectile Motion and Conservation of Energy - College Physics

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Projectile MotionPhysics EducationParabolic TrajectoryKinematic EquationsVelocity CalculationHeight and SpeedProfessor AndersonBuilding LaunchGravity EffectsEducational ContentPhysics Problem Solving