How To Solve Projectile Motion Problems In Physics
TLDRThis video script offers an in-depth exploration of projectile motion, focusing on the kinematic equations for constant speed and acceleration. It explains the concepts of displacement, velocity, and acceleration, and how they change over time. The script uses examples of a ball being kicked and traveling through the air to illustrate how horizontal and vertical velocities vary, and how speed, despite being the magnitude of velocity, behaves differently. The video also discusses three types of projectile trajectories and provides equations for calculating height, range, and time of flight, emphasizing the importance of understanding the distinction between speed and velocity in these contexts.
Takeaways
- 📚 Kinematic equations are essential for understanding projectile motion, with displacement (d) being the key variable.
- 🏃♂️ At constant speed, displacement (d) equals velocity (v) times time (t), while under constant acceleration, d is average velocity (v_avg) times t, with v_avg being the average of initial (v_initial) and final (v_final) velocities.
- 📈 The final velocity (v_final) can be calculated using v_final = v_initial + a*t, where 'a' is the acceleration and 't' is time.
- 🚀 The relationship between initial and final velocities, and displacement is given by the equation v_final^2 = v_initial^2 + 2*a*d.
- 📊 Displacement and distance are the same when an object moves in a single direction; however, they differ when the direction changes.
- 🎾 Projectile motion is influenced only by gravity, ignoring air resistance, making it a simplified model of real-world motion.
- 📉 The vertical velocity (v_y) changes due to gravitational acceleration (a_y), decreasing by 10 m/s every second in the given example.
- 🔄 The speed of an object in projectile motion is the magnitude of its velocity and is always positive, while velocity can be positive or negative.
- 🌐 There are three common projectile trajectories: horizontal motion off a cliff, motion kicked at an angle, and motion thrown straight up or down.
- 🔢 The height of a cliff can be calculated using h = 0.5 * a * t^2, and the horizontal range using r = v_x * t, where v_x is the horizontal velocity component.
- 🕒 The time it takes for a projectile to hit the ground can be found using quadratic equations or by analyzing the motion in segments for complex scenarios.
Q & A
What are the kinematic equations for constant speed and constant acceleration?
-For constant speed, the displacement (d) is equal to velocity (v) multiplied by time (t). For constant acceleration, displacement is equal to the average velocity (v_avg) multiplied by time, where v_avg is the average of the initial (v_initial) and final (v_final) velocities, calculated as (v_initial + v_final) / 2.
How does the vertical velocity of a projectile change over time under constant acceleration due to gravity?
-The vertical velocity (v_y) changes by the gravitational acceleration (a) every second. If the gravitational acceleration is -9.8 m/s^2, the vertical velocity decreases by 9.8 m/s every second.
What is the difference between displacement and distance in the context of projectile motion?
-Displacement is the change in position and can be along the x or y axis, while distance is the total path length traveled. Distance and displacement are the same if the object moves in one direction without changing direction. However, if the direction changes, as in projectile motion, displacement and distance differ.
How can you find the height (h) of a projectile when it hits the ground?
-The height (h) can be found using the equation h = (1/2) * a * t^2, where a is the acceleration due to gravity and t is the time it takes for the projectile to hit the ground.
What is the relationship between speed and velocity in the context of projectile motion?
-Speed is the magnitude of velocity and is always positive, while velocity can be positive or negative depending on the direction of motion. In projectile motion, as the object moves upward, the velocity decreases, but the speed first decreases and then increases as the object falls back down.
What are the three types of projectile motion trajectories discussed in the script?
-The three types of trajectories are: 1) A ball rolling off a cliff and falling down, 2) A ball kicked off the ground, reaching a maximum height before falling back down, and 3) A ball kicked off at an angle, going up and then back down.
How can you calculate the range of a projectile motion where the object moves horizontally off a cliff?
-The range (r) can be calculated using the equation r = v_x * t, where v_x is the horizontal velocity component and t is the time it takes for the object to hit the ground.
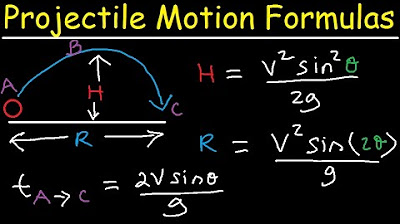
What is the maximum height (H) reached by a ball kicked at an angle?
-The maximum height (H) can be calculated using the equation H = (v^2 * sin^2(theta)) / (2 * g), where v is the initial velocity, theta is the angle relative to the horizontal, and g is the acceleration due to gravity.
How can you find the final speed of a projectile just before it hits the ground?
-The final speed can be found using the equation v = sqrt(v_x^2 + v_y^2), where v_x is the constant horizontal velocity component and v_y is the final vertical velocity component, which can be found using the initial vertical velocity and the time of flight.
What is the time of flight for a ball rolling off a cliff and hitting the ground?
-The time of flight can be calculated using the equation t = sqrt((2 * h) / g), where h is the height of the cliff and g is the acceleration due to gravity.
How does the initial speed of a ball dropped from rest compare to the time it takes to hit the ground compared to when it is thrown downwards with an initial speed?
-A ball dropped from rest will take longer to hit the ground compared to when it is thrown downwards with an initial speed. The initial speed reduces the time of flight because it adds to the velocity that gravity imparts to the ball.
Outlines
📚 Kinematic Equations and Projectile Motion Basics
This paragraph introduces the foundational concepts of projectile motion, emphasizing the kinematic equations for constant speed and acceleration. It explains displacement as velocity times time and how average velocity factors into the equation. The paragraph also covers the relationship between final and initial velocities, and how they relate to time and acceleration. The concept of displacement along the x and y axes is discussed, differentiating between distance and displacement based on direction change. The example of a ball being kicked and how its velocities change over time is used to illustrate these principles, with a focus on gravitational acceleration's role in vertical motion.
🚀 Understanding Velocity and Speed in Projectile Motion
The paragraph delves into the distinction between velocity and speed, clarifying that velocity is vector quantity with both magnitude and direction, while speed is a scalar with only magnitude. It discusses how the vertical velocity changes due to gravitational acceleration, while the horizontal velocity remains constant. The paragraph also addresses the trajectory of projectiles under gravity's influence, ignoring air resistance, and differentiates between projectiles and non-projectiles, such as a flying bird. The concept of speed being always positive while velocity can be negative is highlighted, along with the trajectory types and their characteristics.
📐 Calculating Trajectories: Height, Range, and Velocity
This section focuses on the mathematical aspects of projectile motion, providing formulas for calculating height, range, and final velocity. It explains how to find the height of a cliff using the equation h = 1/2 * a * t^2 and the horizontal range using v_x * t. The paragraph introduces the concept of initial and final velocities in the context of a ball kicked at an angle, and how to use these to calculate maximum height and range. The relationship between the components of velocity and the resultant velocity is also discussed, using trigonometric ratios and the Pythagorean theorem to derive equations for final speed and the angle of projection.
🕒 Time and Velocity Analysis for Different Trajectories
The paragraph examines the time it takes for a projectile to travel from one point to another in different scenarios, such as from the ground to the maximum height and back down to the ground. It provides equations for calculating these times and explains the symmetry of the projectile's path. The maximum height and range equations are derived from the initial velocity and angle of projection. The paragraph also touches on the importance of understanding that the speed at the same height remains constant, despite the change in velocity's direction. Additional equations for calculating the time to hit the ground and the final speed before impact are introduced, emphasizing the practical application of these concepts.
📊 Solving Quadratic Equations for Projectile Motion
This paragraph discusses the application of quadratic equations to find the time of flight in projectile motion scenarios. It provides a step-by-step approach to solving for time using the quadratic formula, incorporating the acceleration due to gravity and the initial conditions. The explanation includes how to handle negative values and the significance of the resulting time in the context of projectile motion. The paragraph also addresses the calculation of the final vertical velocity and the final speed of the projectile before it hits the ground, using the derived equations and the components of velocity.
🎾 Practical Problems in Projectile Motion
The paragraph presents practical problems involving projectile motion, such as a ball rolling off a cliff and the time it takes to hit the ground. It applies the previously discussed concepts and equations to solve for the height of the cliff, the horizontal distance traveled, and the time of flight. The problems vary in complexity, including scenarios with initial velocity and those released from rest. The solutions demonstrate the integration of kinematic equations, quadratic formula, and the understanding of velocity and speed in calculating the trajectory and impact parameters of a projectile.
Mindmap
Keywords
💡Projectile Motion
💡Kinematic Equations
💡Constant Acceleration
💡Displacement
💡Velocity
💡Acceleration
💡Gravitational Acceleration
💡Speed
💡Trajectories
💡Range
💡Height
Highlights
The video is an updated version on the topic of projectile motion.
The kinematic equations are fundamental to understanding projectile motion.
Displacement is calculated as velocity multiplied by time under constant speed conditions.
Under constant acceleration, displacement is calculated using the average velocity multiplied by time.
The final velocity can be determined by the initial velocity plus the product of acceleration and time.
The vertical velocity changes by the gravitational acceleration each second, which is approximately -10 m/s².
The horizontal velocity remains constant in projectile motion due to zero acceleration in the horizontal direction.
Projectile motion is only influenced by gravity and ignores air resistance.
Speed is the magnitude of velocity and is always positive, while velocity can be positive or negative.
The three types of projectile motion trajectories are explained: off a cliff, kicked at an angle, and kicked off a building.
The equations for calculating height and range in projectile motion are derived from the basic kinematic equations.
The maximum height and range of a projectile can be calculated using the initial velocity and launch angle.
The speed at the same height in a projectile's trajectory remains the same due to symmetry.
The quadratic equation is used to find the time it takes for a projectile to hit the ground when given the initial conditions.
The final speed of a projectile just before impact can be calculated using the final vertical and constant horizontal velocities.
The angle of a projectile's trajectory can be found using the ratio of the vertical and horizontal components of velocity.
Examples are provided to calculate the height of a cliff and the time it takes for a ball to hit the ground in different projectile scenarios.
The practical application of the kinematic equations is demonstrated through step-by-step problem-solving.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: