introduction to projectile motion
TLDRThis video script delves into the fascinating world of projectile motion, debunking the common misconception that a horizontally thrown stone with greater speed will take longer to land than one dropped vertically. It explains that both stones will land simultaneously due to the constant vertical acceleration caused by gravity. The script further explores the parabolic trajectory of a projectile, emphasizing that the horizontal velocity remains unchanged while the vertical velocity is affected by gravity. It also introduces the concept of maximum range, which occurs when a projectile is launched at a 45-degree angle, as this is when the horizontal velocity and time in the air are optimally balanced. The video aims to educate viewers on the principles of physics that govern the motion of objects in the air.
Takeaways
- 🌐 Both stones dropped vertically and thrown horizontally at great speed will land at the same time due to the same initial vertical velocity.
- 📉 Projectile motion involves an object following a parabolic path due to the influence of gravity acting vertically on the object's horizontal and vertical velocity components.
- 🔄 The horizontal component of velocity remains constant throughout the motion, while the vertical component is affected by gravity, causing a curved trajectory.
- 🚀 When a ball is thrown at an angle, its trajectory is curved because the vertical velocity decreases due to gravity, while the horizontal velocity remains unchanged.
- 🏆 The maximum range of a projectile is achieved when it is launched at a 45-degree angle, as this is the point where the product of horizontal velocity and time in the air is maximized.
- 🔽 At the peak of its trajectory, the vertical velocity of the projectile is zero before it starts descending with an increasing vertical velocity due to gravity.
- 🧐 The speed at which a stone is thrown horizontally does not affect the time it takes to hit the ground; only the vertical component of velocity is relevant for this timing.
- 🤔 The misconception that a faster horizontally thrown stone will take longer to land is incorrect because the horizontal velocity does not influence the vertical descent.
- 📊 The trajectory's shape is influenced by the variation of the vertical component of velocity over time, with the object taking a curved path as it travels through the air.
- 🎯 Understanding projectile motion allows for the accurate prediction of when and where an object will land, based on its initial velocity components and the acceleration due to gravity.
Q & A
What is the initial condition for both stones thrown off the cliff?
-Both stones are thrown with a vertical component of velocity at the beginning, which is zero.
How does the horizontal velocity of a projectile change during its motion?
-The horizontal component of velocity does not change during the motion of a projectile, as there is no force acting in the horizontal direction.
What is the shape of the trajectory of a projectile affected by gravity?
-The trajectory of a projectile affected by gravity is a parabolic path.
Why does the stone thrown horizontally take the same time to land as the stone dropped straight down?
-Both stones land at the same time because the time it takes for an object to hit the ground depends only on its vertical component of velocity, which is the same for both stones at the start.
What happens to the vertical component of velocity during the projectile's motion?
-The vertical component of velocity changes due to the effect of gravity; it increases as the object falls and decreases as it rises.
What is the maximum height an object can achieve in projectile motion?
-The maximum height is achieved when the vertical velocity becomes zero, which is the highest point in the parabolic trajectory.
Why does the range of a projectile decrease when the angle of projection is greater than 45 degrees?
-The range decreases because the time the object spends in the air decreases as the angle increases, and the horizontal velocity, despite increasing, does not compensate for the reduced time.
What is the relationship between the angle of projection and the range of a projectile?
-The range is maximum when the projectile is thrown at an angle of 45 degrees because both the horizontal velocity and the time in the air have optimal values.
How does the concept of projectile motion explain the misconception about the two stones landing time?
-Projectile motion demonstrates that the horizontal speed does not affect the time it takes for an object to land when thrown horizontally; it's the vertical component of velocity that determines the landing time.
What is the significance of the 45-degree angle in projectile motion?
-The 45-degree angle is significant because it provides the maximum range for a projectile, as it is the angle where the product of horizontal velocity and time in the air is the greatest.
How does the trajectory of a projectile change with variations in the vertical component of velocity?
-The trajectory changes from a straight line to a curved path as the vertical component of velocity decreases due to gravity, resulting in a parabolic shape.
Outlines
🌐 Introduction to Projectile Motion
This paragraph introduces the concept of projectile motion by presenting a scenario where two stones are thrown from a cliff - one dropped vertically and the other horizontally at high speed. It challenges the common intuition that the faster stone would take longer to land by revealing that both stones will actually land at the same time. The explanation delves into the fundamental concepts of projectile motion, highlighting the parabolic path created due to the effects of gravity on an object thrown at an angle. It explains that while the horizontal component of velocity remains constant, the vertical component is affected by gravity, leading to a curved trajectory. The paragraph also discusses how the vertical component of velocity changes over time, resulting in the maximum height and subsequent descent of the object. It concludes with a thought experiment involving a cannon and demonstrates how the angle of projection affects the range of the projectile, revealing that the maximum range is achieved at a 45-degree angle.
🎥 Conclusion and Final Thoughts
The final paragraph wraps up the video by reiterating the intriguing nature of projectile motion and its real-world implications. It thanks the viewer for watching and expresses hope that the content was enjoyable and informative. The paragraph concludes with an invitation to join for the next video, indicating a continuation of the exploration of physics concepts.
Mindmap
Keywords
💡Projectile Motion
💡Parabolic Path
💡Gravity
💡Horizontal Velocity
💡Vertical Velocity
💡Time of Flight
💡Maximum Range
💡Angle of Projection
💡Velocity Components
💡Trajectory
Highlights
Both stones will land at the same time despite the difference in horizontal speed.
Projectile motion involves an object following a parabolic path due to gravity.
When a ball is thrown at an angle, it has two components of velocity: horizontal and vertical.
The horizontal component of velocity remains constant throughout the motion.
The vertical component of velocity changes due to the force of gravity.
The maximum height of the projectile is reached when the vertical velocity becomes zero.
During descent, the vertical velocity increases because gravity and velocity are in the same direction.
The shape of the projectile's trajectory is a parabola.
A ball thrown vertically will return to its initial position with zero horizontal movement.
Reducing the angle of projection increases the horizontal travel of the ball.
The range of the ball increases with angle reduction up to 45 degrees.
The maximum range is achieved at an angle of 45 degrees.
Beyond 45 degrees, the range decreases as the angle increases.
The maximum range occurs when the time in the air and horizontal velocity have optimal values.
The time it takes for the stone to hit the ground depends only on its vertical velocity.
The horizontal velocity given to the stone does not affect its travel time when thrown horizontally.
Transcripts
Browse More Related Video

Solving Projectile Motion Problems in Physics - [1-4-7]
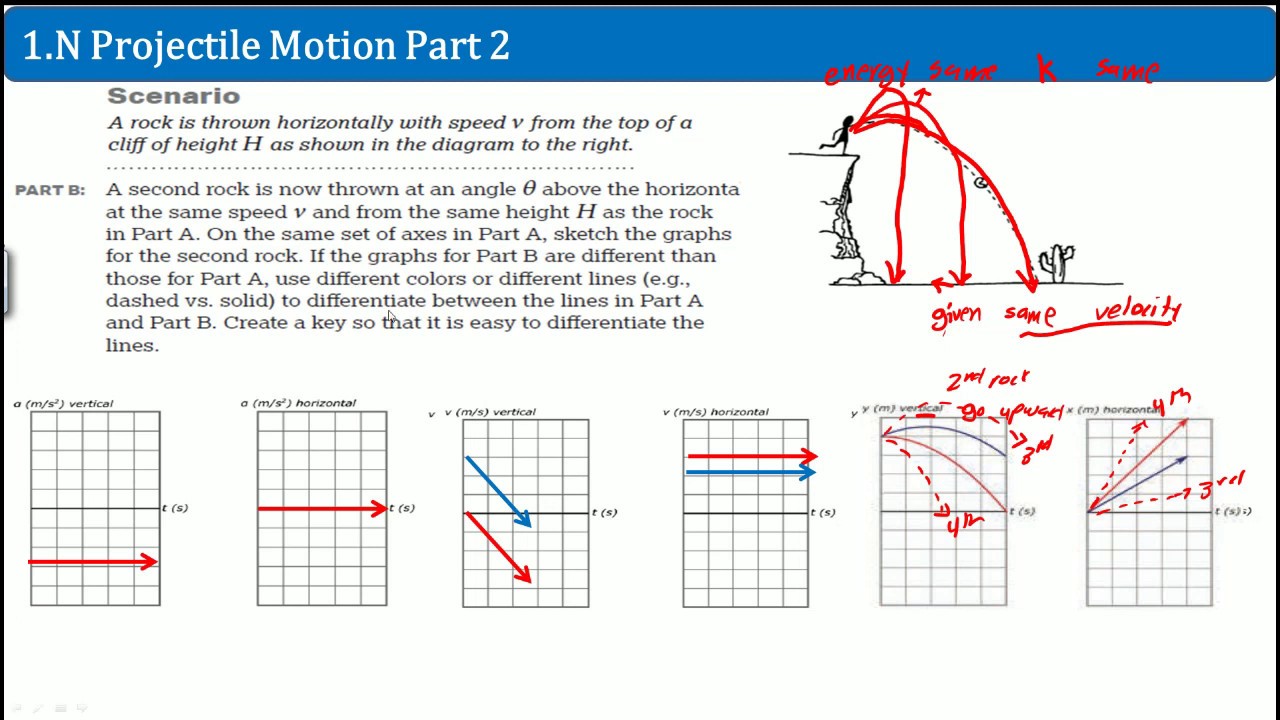
AP Physics 1 Workbook 1.N Projectile Motion Part 2 Solution

AP Physics B Kinematics Presentation #71
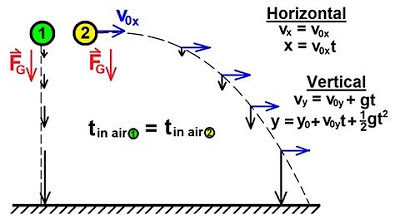
Physics 3: Motion in 2-D Projectile Motion (1 of 21) Independent Motion in x and y
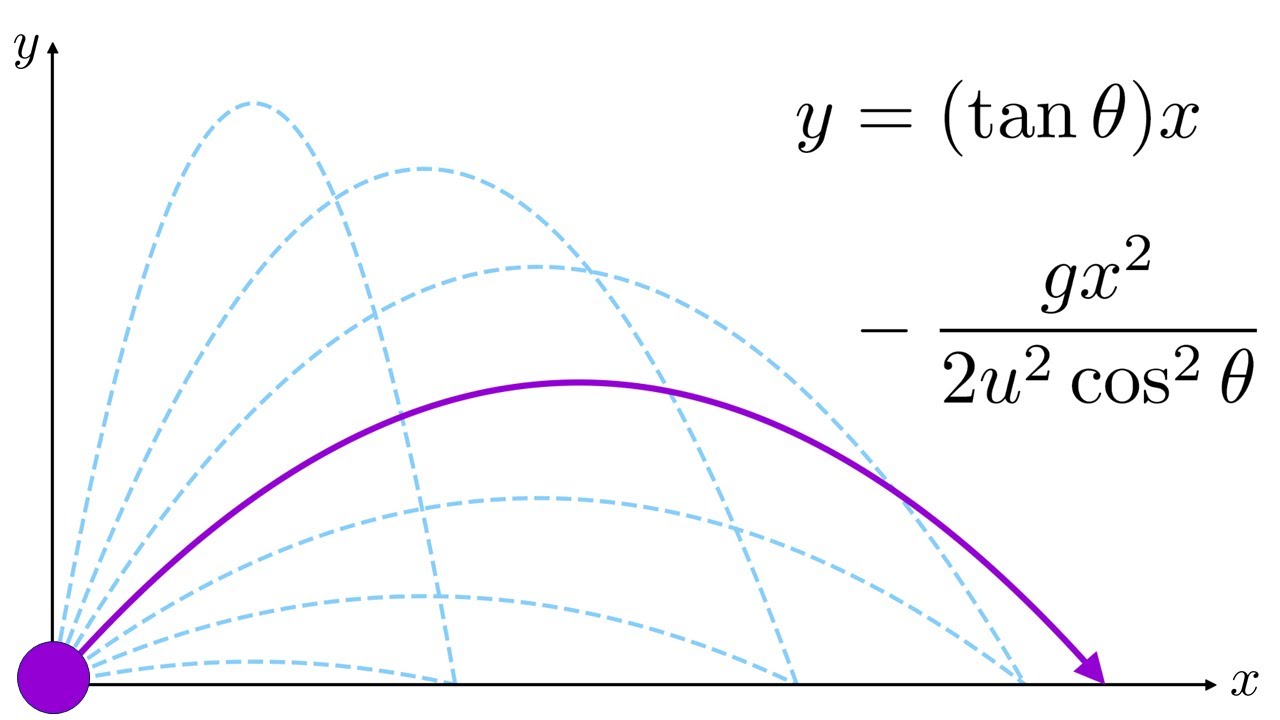
Trajectory of a projectile without drag

The Classic Bullet Projectile Motion Experiment
5.0 / 5 (0 votes)
Thanks for rating: