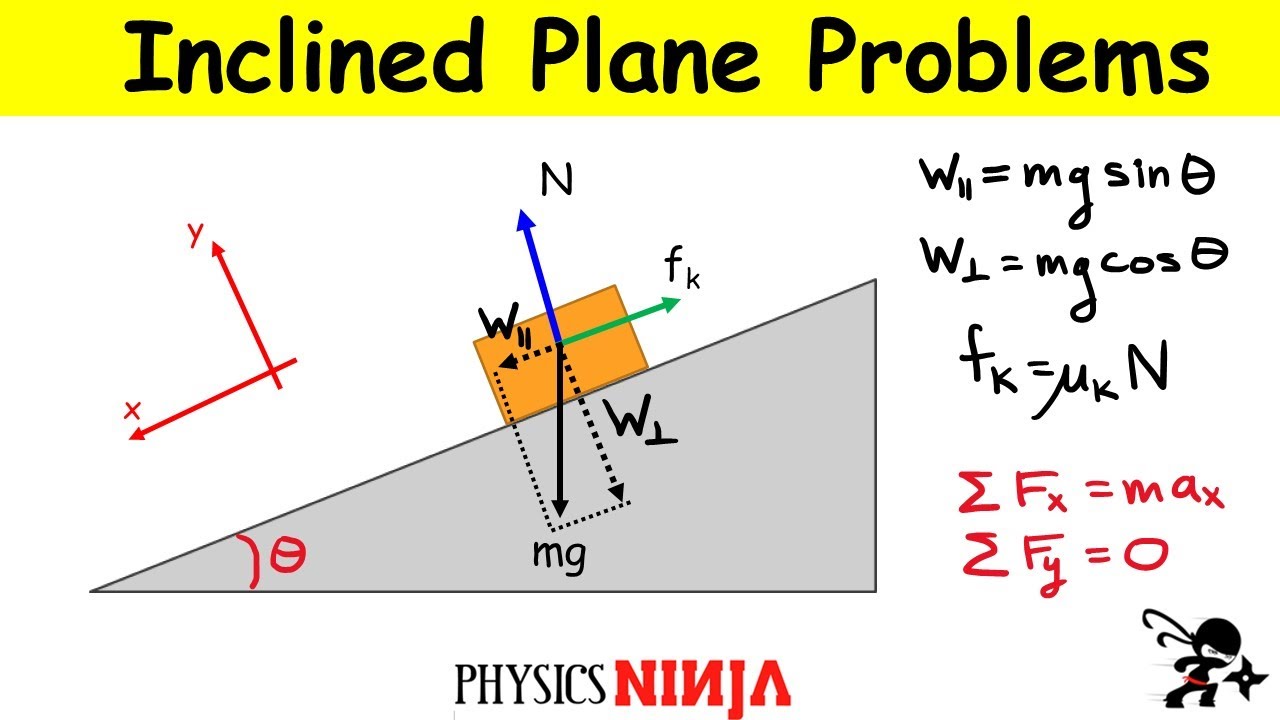
Introduction to Inclined Planes
TLDRThis video script delves into the physics of inclined planes, explaining the forces at play when an object rests on or moves along an incline. It introduces the concepts of normal force, gravitational force components (fg and fn), and their relationships with the angle of inclination. The script uses trigonometric principles (SOHCAHTOA) to derive equations for the normal force (mg cos θ) and the force accelerating the block down the incline (mg sin θ). It further explores scenarios with friction, calculating acceleration with and without it, and provides examples of a block sliding down and up an incline, complete with equations and problem-solving steps. The video aims to enhance understanding of inclined plane dynamics and frictional forces in physics.
Takeaways
- 📚 The normal force (Fn) on an inclined plane is equal to the weight of the object (mg) times the cosine of the incline angle (θ).
- 📐 The force component (Fg) that accelerates the object down the incline is mg times the sine of the incline angle (θ).
- 🚀 The acceleration (a) of an object sliding down a frictionless incline is g times the sine of the incline angle (θ), independent of the object's mass.
- 🔄 When considering friction, the net force (F) in the x-direction is the component of gravitational force (Fg) minus the kinetic friction force (Fk).
- 📈 The acceleration of an object on an incline with friction is given by g sine θ - μk g cosine θ, where μk is the coefficient of kinetic friction.
- 🔺 For an object sliding up an incline, the net force and thus acceleration depend on the direction of motion relative to the incline.
- 📌 The acceleration of a block starting from rest and sliding down a 30-degree incline is 4.9 m/s².
- 🏁 The final speed of a block sliding down a 30-degree incline over a distance of 200 meters is 44.27 m/s.
- 🛤️ A block traveling up a 25-degree incline with an initial speed of 14 m/s has a deceleration of approximately -4.14 m/s².
- 📍 The block traveling up a 25-degree incline will stop after covering a distance of approximately 23.662 meters.
- ⏳ It takes about 3.38 seconds for the block to come to a complete stop after traveling up a 25-degree incline from an initial speed of 14 m/s.
Q & A
What are the main components of force acting on a box resting on an inclined plane?
-The main components of force acting on a box resting on an inclined plane are the normal force, which acts perpendicular to the surface, and the force of gravity, which can be resolved into two components: one parallel to the incline (fg) and one perpendicular to the incline (not explicitly named in the script).
How is the normal force calculated on an inclined plane?
-The normal force on an inclined plane is calculated using the equation: normal force = mg * cos(theta), where m is the mass of the box, g is the acceleration due to gravity, and theta is the angle of inclination.
What is the force component (fg) that accelerates the block down the incline?
-The force component (fg) that accelerates the block down the incline is calculated as: fg = mg * sin(theta), where mg is the weight of the block and theta is the angle of inclination.
How can you find the acceleration of a block sliding down a frictionless inclined plane?
-The acceleration of a block sliding down a frictionless inclined plane is found using the equation: acceleration = g * sin(theta), where g is the acceleration due to gravity and theta is the angle of inclination.
What is the relationship between the frictional force (fk) and the normal force when dealing with an inclined plane?
-The frictional force (fk) is related to the normal force by the equation: fk = mu_k * normal force, where mu_k is the coefficient of kinetic friction and the normal force is calculated as: normal force = mg * cos(theta).
How does the presence of friction affect the acceleration of a block on an inclined plane?
-When friction is present, the acceleration of a block on an inclined plane is affected by subtracting the frictional force (fk) from the component of the gravitational force (fg). The equation for acceleration becomes: acceleration = g * sin(theta) - mu_k * g * cos(theta).
What is the acceleration of a block sliding up an incline compared to sliding down?
-When a block is sliding up an incline, the acceleration is in the opposite direction to sliding down. It is calculated as: acceleration = -g * sin(theta) - mu_k * g * cos(theta), where the negative sign indicates the direction is opposite to the positive x direction (up the incline).
How can you calculate the final speed of a block sliding down an incline from rest?
-To calculate the final speed of a block sliding down an incline from rest, you can use the kinematic equation: v_final^2 = v_initial^2 + 2 * a * d, where v_initial is the initial speed (zero in this case), a is the acceleration down the incline, and d is the distance traveled.
What is the distance a block will travel up an incline before coming to a stop?
-To find the distance a block will travel up an incline before coming to a stop, use the kinematic equation: v_final^2 = v_initial^2 + 2 * a * d. Rearrange the equation to solve for d, with v_final being zero (since the block comes to a stop), v_initial being the initial speed, and a being the deceleration due to gravity and friction.
How long will it take for a block to come to a complete stop after traveling up an incline?
-To determine the time it takes for a block to come to a complete stop after traveling up an incline, use the kinematic equation: v_final = v_initial + a * t. Solve for t by substituting the known values, including the final speed (zero), initial speed, and acceleration (negative value due to the block slowing down).
How does the angle of inclination affect the acceleration of a block on an inclined plane?
-The angle of inclination directly affects the acceleration of a block on an inclined plane. As the angle increases, the sine of the angle also increases, leading to a higher acceleration down the incline, calculated by the equation: acceleration = g * sin(theta).
What is the significance of the trigonometric ratios (SOHCAHTOA) in analyzing inclined plane problems?
-The trigonometric ratios (SOHCAHTOA) are crucial in analyzing inclined plane problems as they help in breaking down the gravitational force into components parallel (opposite) and perpendicular to the incline. Sine, cosine, and tangent ratios are used to relate the forces acting on the block to the angle of inclination and the weight of the block.
Outlines
📚 Inclined Planes and Basic Forces
This paragraph introduces the concept of inclined planes and the forces involved when an object rests on an incline. It explains the normal force (perpendicular to the surface) and its relationship with the gravitational force. The speaker uses trigonometric principles to derive the equations for the components of gravitational force acting along the incline (mg cosine theta for the normal force and mg sine theta for the force accelerating the object down the incline). The importance of understanding these relationships is emphasized for solving problems related to inclined planes.
🚀 Calculating Acceleration on Inclined Planes
The speaker delves into calculating the acceleration of an object sliding down a frictionless incline. Using Newton's second law, the acceleration is derived to be g sine theta, which is dependent only on the angle of the incline and not on the mass of the object. The paragraph then discusses the presence of friction and how it affects the acceleration, introducing the formula for net force considering kinetic friction. The speaker also explains how to calculate the acceleration when an object is sliding up an incline, highlighting the change in direction of forces but not in the principles used.
📐 Solving a Physics Problem: Block Sliding Down
The speaker presents a practical physics problem involving a block sliding down a 30-degree incline from rest. The net force acting on the block is calculated, leading to the determination of the block's acceleration using the previously derived formulas. The acceleration is found to be 4.9 meters per second squared. The problem is further solved to find the block's final speed after traveling 200 meters down the incline, using the kinematic equation v^2 = u^2 + 2as. The final speed is calculated to be 44.27 meters per second.
🧗♂️ Block Moving Up an Inclined Plane
The paragraph shifts focus to a block moving up a 25-degree incline with an initial speed. The acceleration of the block as it moves up is calculated, taking into account the gravitational force acting against its motion. The acceleration is found to be negative 4.14166 meters per second squared. The speaker then addresses how far the block will travel up the incline before coming to a stop, using the kinematic equation and calculating the displacement to be 23.662 meters.
⏱️ Time Taken for Block to Stop
The final part of the problem is solved by determining the time it takes for the block moving up the incline to come to a complete stop. Using the kinematic equation v = u + at, the time is calculated by rearranging the formula to solve for t, given the initial speed, final speed (zero), and acceleration. The time calculated is 3.38 seconds, providing the duration for the block to stop after starting with an initial speed of 14 meters per second on a 25-degree incline.
Mindmap
Keywords
💡Inclined Planes
💡Normal Force
💡Gravitational Force
💡Trigonometry
💡Acceleration
💡Friction
💡Net Force
💡Kinematic Formulas
💡Coefficient of Kinetic Friction (mu k)
💡SOHCAHTOA
Highlights
Review of inclined plane formulas and their applications in physics.
Explanation of normal force and its relationship with the angle of inclination.
Use of trigonometry (SOHCAHTOA) to determine the components of force on an inclined plane.
Formula for the component of weight force (fg) that accelerates a block down the incline.
Derivation of the acceleration of a block on an incline without friction.
Inclusion of friction in the analysis and its effect on the acceleration of a block.
Calculation of the acceleration of a block sliding up an incline.
Explanation of how the direction of motion affects the forces and acceleration.
Real-world physics problem involving a block sliding down a 30-degree incline from rest.
Determination of the block's acceleration using the derived formulas.
Calculation of the final speed of a block after traveling a certain distance down an incline.
Application of kinematic formulas to solve for distance and time in incline-related problems.
Comprehensive example of solving for acceleration, distance, and time for a block on a 25-degree incline.
Explanation of how to handle negative acceleration in incline problems.
Use of Newton's second law to analyze the net force and derive acceleration in incline scenarios.
Discussion on the effect of friction on the motion of a block moving up or down an incline.
Final example illustrating the stoppage of a block moving up an incline and the time taken to stop.
Transcripts
Browse More Related Video
How to Solve Inclined Plane Problems

Free body diagram sine and cosine components

AP Physics 1 Work and Energy Practice Problems and Solutions
Banked Turn with Friction - Physics of Speed Limits on Banked Curves

Normal Force Physics Problems With Tension, Inclined Planes & Free Body Diagrams

AP® Physics 1: Forces and Newton's Laws (Unit 2)
5.0 / 5 (0 votes)
Thanks for rating: