Physics | Work, Energy & Power | Part 1 (Work done)

Mlungisi Nkosi

17 Apr 202052:11

EducationalLearning

32 Likes 10 Comments

TLDRThe video lesson delves into the concepts of work, energy, and power, focusing on work done by various forces such as applied force, friction, gravity, and normal force. It clarifies misconceptions around the angle theta in work calculations and provides examples, including a detailed analysis of work done on an inclined plane, emphasizing the importance of Freebody diagrams and vector components in understanding the work done by different forces acting on a system.

Takeaways

📘 The definition of work done involves the product of a force and displacement in the direction of the force.
🔢 Work done is calculated as the force multiplied by displacement (W = F * d), with consideration of the angle (θ) between the force and displacement vectors.
📐 When the force and displacement are in the same direction (θ = 0°), the work done is positive and equal to the product of the magnitudes (cos 0° = 1).
📉 When the force and displacement are in opposite directions (θ = 180°), the work done is negative, indicating energy lost or transformed in the system (cos 180° = -1).
🔄 The work done by gravity depends on the direction of the displacement; no work is done when there is no displacement in the direction of the gravitational force.
🔄 The normal force does no work when there is no displacement in the direction perpendicular to the surface.
🔄 In the context of an inclined plane, the work done by the applied force, friction, and gravity must be calculated with respect to the incline angle.
📊 The net work done on an object is the sum of the work done by individual forces or can be calculated using the net force and displacement.
🔄 Negative work indicates that energy is removed from the system, such as when friction opposes motion and converts mechanical energy into heat.
🔄 The perpendicular and parallel components of gravitational force on an incline affect the calculation of work done differently.
📘 The concept of work, energy, and power is essential for understanding the conservation of mechanical energy, which will be further explored in subsequent lessons.

Q & A

What is the definition of work done?
-Work done is defined as the product of a force and displacement in the direction of the force. It occurs when a force causes an object to move in the direction of the force's application.
What are the different types of forces that can be doing work?
-Different types of forces, such as applied force, gravitational force, normal force, and frictional force, can be doing work on an object. Each type of force can contribute differently to the total work done on the object.
How is the angle theta related to the work done by a force?
-The angle theta is the angle between the direction of the force and the direction of displacement. The cosine of theta is used in the work done formula to account for the component of the force that is in the direction of displacement.
What is the significance of negative work done?
-Negative work done indicates that the force is doing work against the direction of motion, leading to a loss of energy from the system. For example, frictional force does negative work as it opposes the motion and converts mechanical energy into heat.
Why does the work done by gravity depend on the direction of displacement?
-The work done by gravity depends on the direction of displacement because gravity is a vertical force, and it only does work when there is displacement in the vertical direction. If there is no vertical displacement, the work done by gravity is zero.
How can the work done by multiple forces be calculated?
-The work done by multiple forces can be calculated by determining the work done by each force individually using the formula (force * displacement * cos(theta)), and then summing these values to find the total work done or net work done on the system.
What is the net work done on an object?
-The net work done on an object is the algebraic sum of the work done by all the individual forces acting on it. It can also be calculated by finding the work done by the net force, which is the vector sum of all the individual forces.
How does the normal force contribute to the work done on an object?
-The normal force is always perpendicular to the surface and to the direction of motion when an object is moving horizontally. Since there is no displacement in the direction of the normal force, it does no work on the object, contributing zero to the net work done.
What is the relationship between work, energy, and power?
-Work is a measure of energy transfer. When work is done on an object, it can change the object's energy, such as its kinetic or potential energy. Power is the rate at which work is done, indicating how quickly energy is transferred or transformed.
Why is it important to understand the work done by different forces?
-Understanding the work done by different forces is crucial for analyzing the energy changes in a system and for solving problems related to mechanical energy, efficiency, and the dynamics of moving objects.
How does the inclined plane scenario affect the work done calculations?
-In an inclined plane scenario, the gravitational force has components parallel and perpendicular to the incline. The work done calculations must account for these components, considering the angle of inclination and the direction of motion along the incline.

Outlines

00:00

📚 Introduction to Work, Energy, and Power

The video begins with an introduction to the concepts of work, energy, and power. The speaker explains that the lesson will focus on work-energy principles, acknowledging that the chapter is extensive and may require a follow-up video. The speaker encourages viewers to contact them with questions via email and to engage with the content by posting comments and subscribing to the channel. The first topic discussed is the definition of work done, which is the product of force and displacement in the direction of the force. The speaker emphasizes the importance of understanding the different types of forces and the associated work done, clarifying misconceptions around the angle θ in work calculations.

05:01

🔍 Freebody Diagrams and Work Calculation

This paragraph delves into the practical application of work concepts using a Freebody diagram. The speaker illustrates how to represent all forces acting on a system and calculates the work done by various forces, including applied force, friction, and gravitational force. The explanation includes the scalar nature of work and the significance of the angle θ between the force and the direction of motion. A detailed example is provided, where a 10 kg block is pulled with a force of 40 Newtons across a rough horizontal surface, and the work done by the applied force and friction is calculated. The speaker also touches on the concept of net work done and the importance of understanding Newton's laws in this context.

10:03

📊 Work Done by Friction and Gravitational Force

The speaker continues the discussion on work by focusing on the work done by friction and gravitational force. Using the previous example, the work done by kinetic friction is calculated, highlighting that it is negative work as it represents energy lost in the system. The speaker also explains the work done by gravitational force, noting that it results in zero work done when there is no displacement in the direction of the force. The explanation includes the calculation of work done by the normal force and how it relates to the perpendicular direction of motion, resulting in zero work done. The paragraph emphasizes understanding the directionality of forces and their impact on work calculations.

15:04

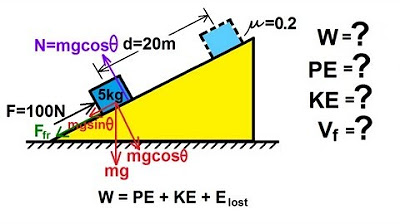
🔧 Calculating Work Done on an Inclined Plane

This section introduces a new scenario involving an inclined plane, where a force is applied to move a block up the incline. The speaker explains the importance of starting with a Freebody diagram to identify all forces acting on the system. The forces discussed include the applied force, frictional force, gravitational force, and the normal force. The speaker provides a detailed breakdown of how to calculate the work done by each force, considering the angle of inclination and the direction of motion. The explanation includes the decomposition of gravitational force into parallel and perpendicular components and how these components affect the work done calculations. The speaker also addresses common misconceptions and provides clarity on the application of trigonometric functions in determining the work done by gravity.

20:06

🚀 Net Work Done and Conservation of Mechanical Energy

The final paragraph synthesizes the concepts discussed throughout the video, focusing on the calculation of net work done. The speaker explains how to determine the net force acting on the block and how to calculate the net work done using either the net force or the sum of individual work done by each force. The concept of work done by the normal force is revisited, emphasizing that it contributes zero joules to the net work done. The speaker also hints at the upcoming topic of conservation of mechanical energy, setting the stage for future lessons. The video concludes with an invitation for viewers to reach out with questions and to engage with the content for further understanding.

Mindmap

Keywords

💡Work

In the context of the video, work is defined as the product of a force and displacement in the direction of the force. It is a measure of energy transfer that occurs when a force moves an object. The video emphasizes the importance of the angle between the force and displacement, using the cosine of this angle (cos(theta)) in calculations. For instance, when the force and displacement are in the same direction, the angle is zero, and cos(0) equals 1, resulting in positive work. Conversely, when the force and displacement are in opposite directions, the angle is 180 degrees, and cos(180) equals -1, resulting in negative work, indicating energy loss due to friction.

💡Energy

Energy in the video refers to the capacity to do work. It is a scalar quantity, meaning it only has magnitude and no direction. The concept of energy is central to the discussion of work, as work is a form of energy transfer. The video touches on how different types of work (like work done by gravity, friction, and applied force) result in different forms of energy either being used or dissipated within a system.

💡Power

Although not explicitly defined in the video, power is related to the rate at which work is done. It is a measure of how quickly energy can be transferred or transformed. In the context of the video, understanding power would involve considering the time taken to do the work discussed, which is not directly addressed but is an important concept in the study of energy and work.

💡Force

A force is any action that can cause an object to change its state of motion or rest. In the video, various types of forces are discussed, including applied force, gravitational force, frictional force, and normal force. The direction and magnitude of these forces are crucial in calculating work done and energy transfer.

💡Displacement

Displacement refers to the change in position of an object. In the context of work, it is the distance the object moves in the direction of the applied force. The video emphasizes that work is the product of the force and the displacement in the direction of the force, highlighting the importance of considering the angle between the force and displacement.

💡Angle (theta)

The angle, often symbolized as theta (θ), is the angle between the direction of the force and the direction of displacement. The cosine of this angle is used in the formula for work to determine the amount of work done by a force. The angle is crucial in understanding whether the force is doing positive work (when force and displacement are in the same direction) or negative work (when they are in opposite directions).

💡Friction

Friction is a force that opposes the relative motion or tendency of such motion of two surfaces in contact. In the video, kinetic friction is mentioned, which is the frictional force acting on a moving object. Friction does negative work on an object, converting mechanical energy into thermal energy (heat).

💡Gravitational Force

The gravitational force is the attractive force that Earth exerts on objects. In the context of the video, this force acts vertically downwards and can be decomposed into two components when dealing with an inclined plane: one perpendicular to the plane and one parallel to it. The work done by gravity depends on its component in the direction of motion.

💡Normal Force

The normal force is the force exerted by a surface as it supports the weight of an object resting on it. This force is perpendicular to the surface. In the video, the normal force is discussed in the context of an inclined plane, where it acts perpendicular to the plane and does no work on the object as there is no displacement in the direction of the normal force.

💡Net Work Done

The net work done is the total amount of work done on an object when considering all the individual forces acting on it. It is calculated by summing the work done by each force or by calculating the work done by the net force (the vector sum of all forces) acting on the object. The net work done is important in understanding the overall energy transfer in a system.

💡Inclined Plane

An inclined plane is a flat surface that is sloped at an angle to the horizontal. In the video, the inclined plane introduces additional complexity in calculating work done as forces acting on the object must be resolved into components parallel and perpendicular to the plane. The angle of inclination is crucial in determining these components and their respective work done.

Highlights

Introduction to the concept of work, energy, and power, emphasizing the importance of understanding the relationship between force, displacement, and the angle of application.

Explanation of the definition of work done, which is the product of a force and displacement in the direction of the force.

Clarification on the impact of different types of forces on the work done, and how the angle theta (θ) plays a role in the calculation of work.

Illustration of a practical example involving a 10 kg block, an applied force of 40 Newtons, and kinetic friction of 20 Newtons, to demonstrate the calculation of work done.

Discussion on the work done by friction, highlighting that it is negative work as it represents energy lost in the system due to opposing motion.

Explanation of how to calculate the work done by gravitational force and normal force, and why these forces can result in zero work done in certain circumstances.

Introduction to the concept of net work done, which is the work done by the net force acting on a system.

Demonstration of how to calculate the work done by the net force, and the importance of considering the direction of motion and the forces involved.

Transition to discussing the application of work energy and power concepts on an inclined plane, including the forces involved and their components.

Explanation of how to break down the force of gravity into perpendicular and parallel components when dealing with an inclined plane.

Illustration of the Freebody diagram for an object on an inclined plane, showing all the forces acting on the system and their respective directions.

Detailed calculation of the work done by the applied force, friction, gravity, and normal force on an inclined plane, emphasizing the method and the significance of each.

Discussion on the importance of understanding the direction of forces and displacement when calculating work done, and how this affects the results.

Explanation of how to calculate the net work done on an inclined plane, and the significance of this in understanding the energy transfer in the system.

Emphasis on the practical application of the concepts of work, energy, and power in solving problems involving inclined planes and the forces involved.

Conclusion of the lesson with a reminder of the importance of practice and the availability of further assistance for understanding the concepts discussed.

Transcripts

Browse More Related Video

AP Physics 1 Work and Energy Practice Problems and Solutions

Energy Systems Clarified

Physics 8 Work, Energy, and Power (7 of 37) Inclined Plane (Friction)

AP Physics C: Work, Energy, and Power Review (Mechanics)

Work Energy and Power Full Topic

How to find the work done by forces on an inclined plane. Work done by friction and a pulling force.

Related Tags

Physics Concepts Work Calculation Energy Analysis Mechanical Energy Frictional Force Inclination Plane Applied Force Net Work Educational Content Physics Tutorial