AP Physics Workbook 2.M Limiting Cases
TLDRThe video script discusses a physics problem involving a sled with a total mass M, friction, and a tension force T applied at an angle theta. It explains how to draw a Freebody diagram, break down the force into components, and apply Newton's second law to calculate the acceleration of the system. The video clarifies that increasing angle theta affects both horizontal and vertical accelerations differently, leading to a decrease in horizontal acceleration as theta approaches 90 degrees and an increase in vertical acceleration. The problem is solved by deriving expressions for the forces and applying them to the equations of motion.
Takeaways
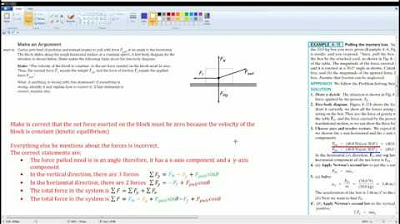
- 📚 The problem involves a sled with a total mass M being pulled by a rope with constant tension T at an angle θ with the horizontal.
- 🔢 The coefficient of kinetic friction between the sled and the ground is μk, which affects the force of friction.
- 🎨 A Freebody diagram is essential for visualizing the forces acting on the sled in both the vertical and horizontal directions.
- 🔄 The force applied (T) has both horizontal (T cos θ) and vertical (T sin θ) components.
- 🔽 The vertical forces include the normal force (N) and the weight of the sled (mg), with N being calculated as mg + T sin θ.
- 🔄 The horizontal force of friction is μ times the normal force (μN) and opposes the direction of the sled's motion.
- 📈 As the angle θ approaches 90 degrees, the horizontal component of the tension force (T cos θ) decreases, leading to reduced horizontal acceleration.
- 📊 Conversely, the vertical component of the tension force (T sin θ) increases as θ approaches 90 degrees, potentially increasing the vertical acceleration.
- 🧮 Newton's second law is applied to find the acceleration of the sled by summing forces in the Y direction and dividing by the mass M.
- 📐 The frictional force is calculated as μ times the normal force (μN) and is subtracted from the horizontal force to find the net force and acceleration.
- 📝 The final expression for acceleration includes the cosine and sine components of the force applied, the frictional force, and is divided by the mass M to get the system's acceleration.
Q & A
What is the scenario described in the transcript?
-The scenario involves Blake accelerating a sled carrying his sister. The sled and sister have a total mass M, and there is a coefficient of kinetic friction μk between the sled and the ground. Blake pulls the sled with a rope that has a constant tension force T at an angle θ with the horizontal.
What is the significance of the angle θ in the problem?
-The angle θ is significant because it determines the direction and component of the tension force T applied to the sled. As θ approaches 90 degrees, the horizontal component of the tension force decreases (cosine of θ approaches 0), while the vertical component (sine of θ) increases, potentially affecting the sled's acceleration and the force balance.
How does the frictional force affect the sled in the horizontal direction?
-The frictional force acts in the opposite direction to the sled's motion. It is calculated as μk times the normal force, which depends on the force of tension T and the angle θ. As θ changes, the horizontal component of the frictional force also changes, affecting the sled's acceleration.
What is the relationship between the tension force T and the normal force in the vertical direction?
-The normal force in the vertical direction is equal to the force of tension T minus the vertical component of the tension force (T sin θ). This relationship is crucial for calculating the frictional force in the horizontal direction.
How does the horizontal component of the tension force change with the angle θ?
-The horizontal component of the tension force is given by T cos θ. As the angle θ increases towards 90 degrees, the cosine of θ decreases, leading to a reduction in the horizontal force exerted by the tension.
What happens to the vertical component of the tension force as θ approaches 90 degrees?
-The vertical component of the tension force, which is T sin θ, increases as θ approaches 90 degrees because the sine of θ approaches 1, leading to an increase in the normal force and potentially the frictional force in the vertical direction.
Why does Angelica suggest that increasing the angle θ would decrease the sled's acceleration?
-Angelica's reasoning is based on the horizontal component of the tension force. As θ increases, the horizontal force (T cos θ) decreases, leading to less force available to accelerate the sled, thus reducing its acceleration.
What does Carlos argue about the effect of increasing the angle θ on the sled's motion?
-Carlos argues that increasing the angle θ would increase the vertical component of the tension force (T sin θ), which could lead to a greater normal force and consequently a larger frictional force in the horizontal direction, potentially increasing the sled's acceleration.
How is the acceleration of the sled calculated using Newton's second law?
-The acceleration of the sled is calculated by applying Newton's second law, which states that the net force in a given direction is equal to the mass times the acceleration in that direction. The net force is the sum of the horizontal components of the tension force and the frictional force, minus the vertical component of the tension force, divided by the total mass M.
What is the expression for the force of friction in the horizontal direction?
-The force of friction in the horizontal direction is given by μk times the normal force, which is the force of tension T minus the vertical component of the tension force (T sin θ).
How does the force of friction in the vertical direction affect the problem?
-The force of friction in the vertical direction is not directly involved in the horizontal motion of the sled. However, it is essential for calculating the normal force, which is required to determine the horizontal force of friction and the overall acceleration of the sled.
What is the significance of breaking down the tension force T into its horizontal and vertical components?
-Breaking down the tension force T into its horizontal and vertical components is crucial for analyzing the forces acting on the sled and calculating its acceleration. The horizontal component (T cos θ) directly contributes to the sled's acceleration, while the vertical component (T sin θ) affects the normal force and the frictional force in the horizontal direction.
Outlines
📚 Introduction to Dynamics and Freebody Diagram
The paragraph introduces the topic of dynamics from the AP Physics workbook, focusing on a specific scenario where a character named Blake accelerates a sled carrying his sister. The sled and its contents have a total mass M, and there is a coefficient of kinetic friction, μk, between the sled and the ground. Blake applies a constant tension force, T, to the rope connected to the sled at an angle, θ, with the horizontal. The paragraph explains the process of drawing a Freebody diagram, breaking down the forces involved and their components in both the vertical and horizontal directions. It emphasizes the importance of understanding the role of the angle θ in determining the horizontal and vertical components of the applied force and the frictional force. The paragraph also discusses how the angle affects the acceleration of the sled and how to calculate the forces using Newton's second law.
📐 Analysis of Forces and Acceleration
This paragraph delves deeper into the analysis of forces acting on the sled from the previous scenario. It explains the vertical and horizontal components of the applied force due to the angle θ. As θ approaches 90 degrees, the cosine of θ approaches zero, reducing the horizontal force component, which affects the sled's acceleration. Conversely, as θ approaches zero, the sine of θ approaches one, increasing the vertical force component, which can lead to an increase in vertical acceleration. The paragraph then proceeds to derive expressions for the forces and acceleration using Newton's second law, providing a step-by-step calculation process. It emphasizes the importance of calculating the normal force first, as it is required for determining the frictional force. The summary concludes with a formula for the system's acceleration, incorporating all the forces and the mass of the system.
Mindmap
Keywords
💡Freebody diagram
💡Dynamics
💡Coefficient of kinetic friction
💡Acceleration
💡Tension force
💡Angle theta
💡Newton's second law
💡Force components
💡Frictional force
💡Mass
Highlights
The scenario involves Blake accelerating a sled carrying his sister, with a total mass M.
The coefficient of kinetic friction between the sled and the ground is denoted as μk.
A constant tension force T is applied to the sled by a rope, making an angle θ with the horizontal.
The problem requires drawing a Freebody diagram to visualize the forces acting on the sled.
The vertical force calculation involves the normal force minus mg and the Y component of the applied force.
The X component of the applied force is the force of friction, which is also dependent on the angle θ.
The horizontal component of the applied force is given by T * cos(θ), and the vertical component by T * sin(θ).
Angelica suggests that increasing the angle θ will decrease the horizontal acceleration of the sled.
Carlos argues that increasing the angle θ will actually increase the sled's acceleration towards the left.
As θ approaches 90 degrees, the cosine of θ goes to 0, reducing the horizontal force component.
As θ approaches 90 degrees, the sine of θ goes to 1, increasing the vertical force component.
The force of friction is calculated as μ * F_normal, which depends on the normal force.
Newton's second law is applied to find the acceleration of the system by considering the net forces in both Y and X directions.
The acceleration of the system is found by dividing the net force by the mass of the system (M).
The final expression for acceleration includes the cosine and sine components of the applied force and the force of friction.
The solution provides a comprehensive understanding of forces, friction, and acceleration in a dynamic system.
The problem demonstrates the practical application of physics principles in analyzing real-world scenarios.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: