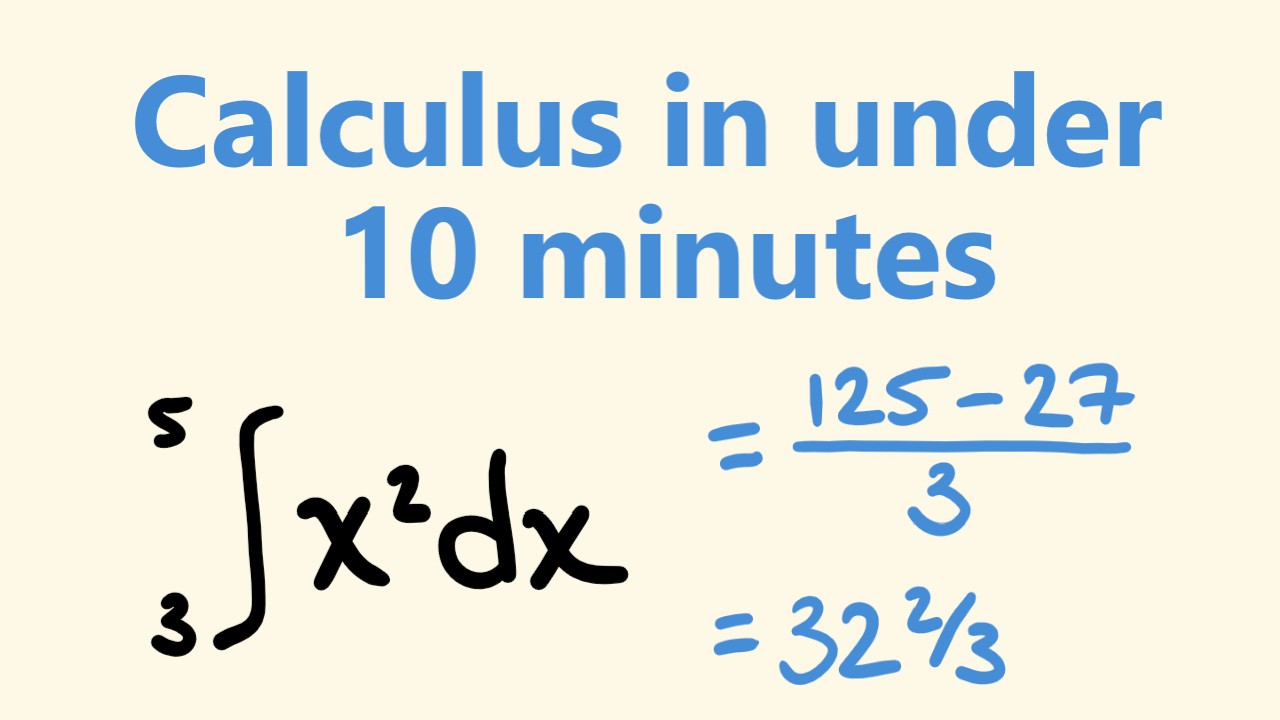Understand Calculus in 10 Minutes
TLDRThis video aims to demystify calculus and reduce its intimidation factor. It explains that calculus is primarily used to solve two types of problems: calculating the area and volume of complex shapes, and determining the slope (or rate of change) of a curve at any given point. The video emphasizes the importance of calculus in various fields such as engineering and science and assures viewers that, despite its complexity, it is learnable with the right approach and understanding of its practical applications.
Takeaways
- 📚 Understanding Calculus: The video aims to demystify calculus and reduce the intimidation factor for students.
- 🎓 Math Pathway: In high school, the typical math pathway leads from Algebra to Calculus, with some students reaching Calculus in their final year.
- 🏛️ College Requirements: Many college majors, especially in science and technical fields, require at least one semester of calculus.
- 📊 Calculus Applications: Calculus is crucial in fields like engineering and science, providing exact solutions for complex problems.
- 🔍 Area and Volume: Calculus helps in determining the area and volume of irregular shapes that don't have straightforward formulas.
- 📈 Curves and Functions: Calculus uses functions to describe curves, allowing for the calculation of areas and volumes under curves.
- 📌 Exact Area Calculation: The integral is used in calculus to find the exact area under a curve, given the function that describes it.
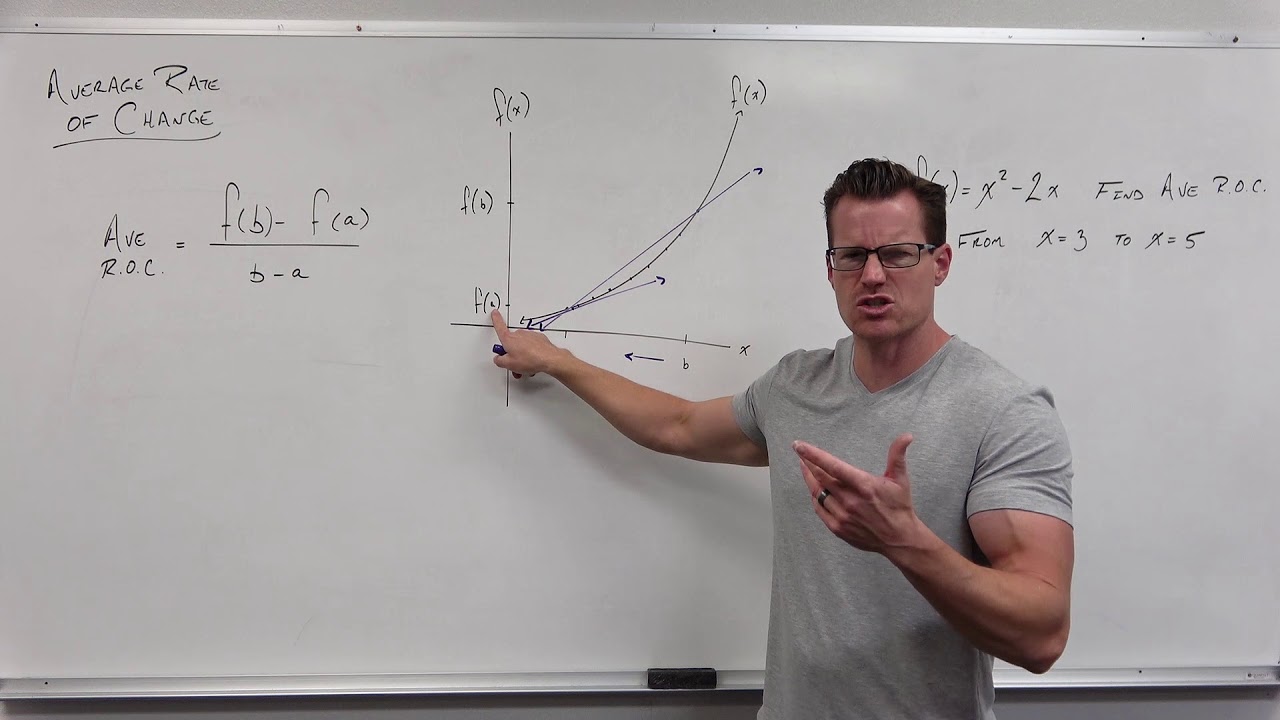
- 🚀 Slope and Derivatives: Calculus is used to find the slope (or steepness) of a curve at any given point, using derivatives.
- 🎯 Precision in Science: Calculus allows for precise determination of rates of change, such as population growth or pharmaceutical effectiveness.
- 📉 Maxima and Minima: Calculus is used to find maximum and minimum values on a curve, which is essential in optimizing various scientific and real-world scenarios.
- 💡 Learning Calculus: Despite its complexity, calculus is learnable even for those who struggle with math, by understanding its value and focusing on learning the rules.
Q & A
What is the main goal of the video?
-The main goal of the video is to demystify calculus and lessen the intimidation factor for students, providing a basic understanding of what calculus is and its applications.
Where does calculus typically fall in the spectrum of math education?
-In high school, calculus usually comes after Algebra one, geometry, Algebra two, and precalculus, typically being studied in the last year of high school. In college, around 70% of majors require at least one semester of calculus.
How does calculus help in solving problems related to area and volume?
-Calculus allows for the calculation of areas and volumes of complex shapes for which there are no straightforward formulas, by using integration to find the exact area under a curve or the volume of a solid generated by rotating a shape around an axis.
What is the significance of calculus in fields like engineering and science?
-Calculus is extremely important in engineering and science as it is used to solve problems involving rates of change and to model and analyze various phenomena, making it a powerful tool for understanding and predicting the behavior of systems.
How does calculus help determine the slope of a curve?
-Calculus uses derivatives to find the exact slope of a curve at any given point, which is essentially the rate of change or steepness of the curve at that point. This is useful for understanding how quantities change over time or in response to other variables.
What is the basic formula for finding the area of a rectangle?
-The basic formula for finding the area of a rectangle is length times width.
What is the formula for finding the area of a circle?
-The formula for finding the area of a circle is πr^2, where r is the radius of the circle.
What does the integral symbol (∫) represent in calculus?
-The integral symbol represents the process of integration in calculus, which is used to find the area under a curve or the volume of a solid generated by rotating a shape around an axis.
What is the general process for finding the area under a curve using calculus?
-The general process involves using integration, where you set up the integral with the function that describes the curve and the limits of integration (the interval from the left side to the right side of the curve), and then apply the rules of integration to find the area.
How does the video describe the process of finding the derivative of a function?
-The video describes the process of finding the derivative as applying a set of rules where you essentially take the exponent of each term in the function, add one to it, and then divide by that number to find the slope of the curve at any point.
What is the purpose of finding the exact slope of a curve at a specific point?
-Finding the exact slope at a specific point helps in understanding the precise rate of change at that moment, which can be crucial in various applications such as determining the optimal dosage of a drug in medical studies or understanding the behavior of populations over time.
Outlines
📚 Introduction to Calculus
This paragraph introduces the concept of calculus and aims to demystify it for viewers. It explains that calculus is not about mastering it in a short time but understanding its essence. The speaker addresses the intimidation factor associated with calculus and provides a brief overview of the typical math curriculum in high school and college, emphasizing the importance of calculus in various fields of study and its prevalence in college courses, especially for science and technical majors.
📊 Calculating Areas and Volumes
The speaker discusses the application of calculus in determining areas and volumes of various shapes, including those with complex geometries that don't have straightforward formulas. It highlights how calculus can be used to find the area under a curve and the volume of revolution of a shape. The paragraph explains the process of using calculus to find the area under a curve by setting up an integral and provides an example of how to calculate the area of a shape without a known formula using calculus.
📈 Understanding Slope and Rate of Change
This paragraph delves into the second major application of calculus: determining the slope or steepness of a curve, which represents the rate of change. The speaker explains how calculus allows for the precise measurement of slope at any point on a curve, which is crucial for understanding trends in various real-world scenarios. The concept of derivatives is introduced as a tool for finding the slope at any given point, and the paragraph outlines the process of finding the derivative of a simple function.
🎯 Maxima, Minima, and Applications
The speaker discusses the use of calculus in identifying maximum and minimum values of functions, which is vital for various scientific studies and practical applications. An example is given where calculus can be used to determine the optimal dosage of a pharmaceutical drug by finding the exact point where the drug is most effective. The paragraph emphasizes the power of calculus in solving complex problems and making precise determinations in scientific research and other fields.
🚀 Wrapping Up Calculus
In the concluding paragraph, the speaker summarizes the key points discussed in the video, reiterating the two main applications of calculus: calculating areas and volumes, and determining slopes and rates of change. The speaker encourages viewers, even those with a weak math background, to approach calculus with the understanding of its value and practical applications. The video ends with a call to action for viewers to subscribe to the channel for more content.
Mindmap
Keywords
💡Calculus
💡Intimidation Factor
💡Area and Volume
💡Functions
💡Derivatives
💡Integrals
💡Slope
💡Mathematical Majors
💡High School Math Curriculum
💡Rate of Change
💡College Education
Highlights
The video aims to demystify calculus and lessen the intimidation factor for students.
Calculus is often perceived as too complicated, but this video seeks to show the big picture.
Calculus is a fundamental subject for many college majors, especially in science, engineering, and finance.
Calculus helps in determining the area and volume of complex figures for which there are no direct formulas.
The importance of calculus in mathematics, engineering, and science cannot be overstated.
Calculus is used to find the exact area under a curve, unlike estimations which are less precise.
The concept of functions is introduced as a way to describe curves in calculus.
The integral is used in calculus to find the area under a curve.
Calculus allows for the determination of the exact slope (steepness) of a curve at any point.
Derivatives are a key concept in calculus, used to find the slope of a curve at any given point.
Calculus has practical applications in various fields, such as determining the effectiveness of a drug in clinical trials.
The video emphasizes that calculus is not impossible to learn, even for those who struggle with math.
The two main applications of calculus are solving area and volume problems, and determining the slope of curves.
The video provides a basic example of how to find the area under a curve using calculus.
The process of finding the derivative of a function is demonstrated to show how the slope can be calculated.
Calculus is presented as a powerful tool for understanding rates of change and making precise calculations.
The video concludes by encouraging viewers to understand the value of calculus and its wide-ranging applications.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: