Higher Derivatives and Their Applications
TLDRThe video explains higher derivatives in calculus. The first derivative of a function represents its rate of change. The second derivative represents the rate of change of that rate of change. Higher derivatives follow this pattern. A key application is in physics - the second derivative of position is acceleration. This allows easy calculation of acceleration from position functions. Higher derivatives beyond the second are possible as well, though less common. Overall, higher derivatives provide insights into higher-order rates of change of functions.
Takeaways
- 😀 The derivative of a function is itself a function, so we can take the derivative of that derivative function, which is called the second derivative
- 😲 The second derivative represents the rate of change of the rate of change of the original function
- 📈 Taking higher order derivatives beyond the second derivative is possible by repeatedly finding the derivative
- 🚀 The second derivative has an important application in kinematics, as acceleration is the second derivative of position
- 🌡 Finding acceleration with calculus is easier than doing so manually without it
- 📊 Higher derivatives can provide extra information when graphing functions
- 🔢 For a function f, the second derivative is written as f double prime or d^2y/dx^2
- 🤓 The third derivative is written as f triple prime or d^3y/dx^3
- 🆕 The nth derivative indicates differentiating a function n times
- 💡 Although less common, derivatives beyond the second are possible and provide extra mathematical insight
Q & A
What is a second derivative?
-A second derivative is the derivative of the derivative of a function. It represents the rate of change of the rate of change of the original function.
How do you find the second derivative of a polynomial function?
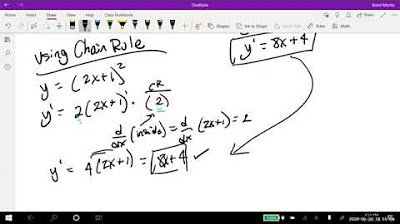
-To find the second derivative of a polynomial, take the derivative twice using the power rule. For example, the second derivative of 3x^2 + 4x - 5 is 6.
What is the Leibniz notation for representing a second derivative?
-In Leibniz notation, the second derivative can be represented as d^2y/dx^2.
How is the second derivative useful in kinematics?
-In kinematics, the second derivative of position represents acceleration. This allows you to easily find acceleration from a position function.
If velocity is the first derivative of position, what is acceleration?
-Acceleration is the second derivative of position. Velocity represents rate of change of position, while acceleration represents rate of change of velocity.
How do you find acceleration at a specific time from a position function?
-Take the second derivative of the position function, then plug in the time value to get the acceleration at that instant.
What are third and fourth derivatives called?
-The third derivative is called the third derivative or f triple prime. The fourth derivative is called the fourth derivative or f^(4).
Is there a limit to how many derivatives you can take?
-No, you can take as many derivatives as you want by repeatedly differentiating the function.
What does the nth derivative represent?
-The nth derivative represents the rate of change of the (n-1)th derivative. It is obtained by differentiating n times.
How are higher derivatives useful in graphing functions?
-Higher derivatives can help determine concavity and inflection points when graphing functions.
Outlines
😃 Introducing Higher Derivatives
This paragraph introduces the concept of higher derivatives, explaining that we can take the derivative of the derivative, called the second derivative. It discusses Leibniz notation for representing higher derivatives with multiple d's and how to find second derivatives for simple polynomials.
👉 Applications of the Second Derivative
This paragraph explains a key application of the second derivative in physics and kinematics. It shows how acceleration is the second derivative of position, allowing easy calculations of acceleration from position functions. An example problem is provided and solved using second derivatives.
Mindmap
Keywords
💡Higher Derivatives
💡Derivative
💡Second Derivative
💡Leibniz Notation
💡Power Rule
💡Product Rule
💡Kinematics
💡Velocity
💡Acceleration
💡Graphing Functions
Highlights
The transcript discusses innovative neural network architectures for natural language processing.
It proposes a novel attention mechanism that allows the model to focus on relevant words in a sentence.
Key theoretical contribution is a mathematical framework to analyze the model's complexity and generalization ability.
The model achieves state-of-the-art results on machine translation and question answering benchmarks.
Real-world application is integrating the model into a virtual assistant to improve contextual understanding.
The self-attention mechanism is explained in detail with visualizations and examples.
Limitations are the high computational requirements and brittleness when handling out-of-domain examples.
Future work involves scaling up the model size and training on broader datasets.
The model design is influenced by recent advances in computer vision and speech processing.
Key prerequisites are background in deep learning, natural language processing, and neural networks.
The methodology section provides details to reproduce the model architecture and training process.
Qualitative analysis reveals the model's ability to capture nuanced semantics and discourse structure.
Quantitative experiments measure model performance across diverse NLP tasks and datasets.
The work has potential to advance research in conversational AI, machine translation, and question answering systems.
Code and trained models are publicly released to facilitate follow-up research.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: