Lesson 6 - Higher Derivatives in Calculus (Calculus 1 Tutor)
TLDRThis educational video script introduces the concept of higher derivatives in calculus. It explains that while first derivatives are commonly studied, it's possible to calculate higher order derivatives by repeatedly differentiating a function. The script clarifies the notation for higher derivatives, such as using d^2y/dx^2 for the second derivative and y'''' for the fourth derivative, emphasizing that these notations are not exponential but indicate the order of differentiation. An example is given where the first and second derivatives of a polynomial function are to be found, illustrating the process and notation.
Takeaways
- 📚 The class is focused on the concept of higher derivatives, building upon the understanding of first derivatives.
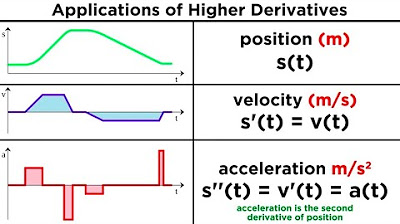
- 🌟 The first derivative of a function is also referred to as the rate of change or the velocity in physical contexts.
- 🔄 Taking the derivative of the first derivative results in the second derivative, which can represent acceleration in a physical scenario.
- 📈 The notation for the first derivative is written as dy/dx or f'(x), indicating the derivative of 'y' with respect to 'x'.
- 🔢 The second derivative is denoted as d²y/dx² or f''(x), with the double prime signifying the second derivative.
- 🏹 Higher derivatives can be represented using a similar notation, with the derivative order indicated by the number of primes or using exponentiation in the variable (e.g., d³y/dx³ or f'''(x) for the third derivative).
- 🎓 The use of parentheses around the variable and derivative order is a convention to avoid confusion with exponents (e.g., d³y/dx³ rather than y³).
- 🌐 Infinite derivatives can be taken in theory, although in practice this often leads to a point where no more information can be obtained.
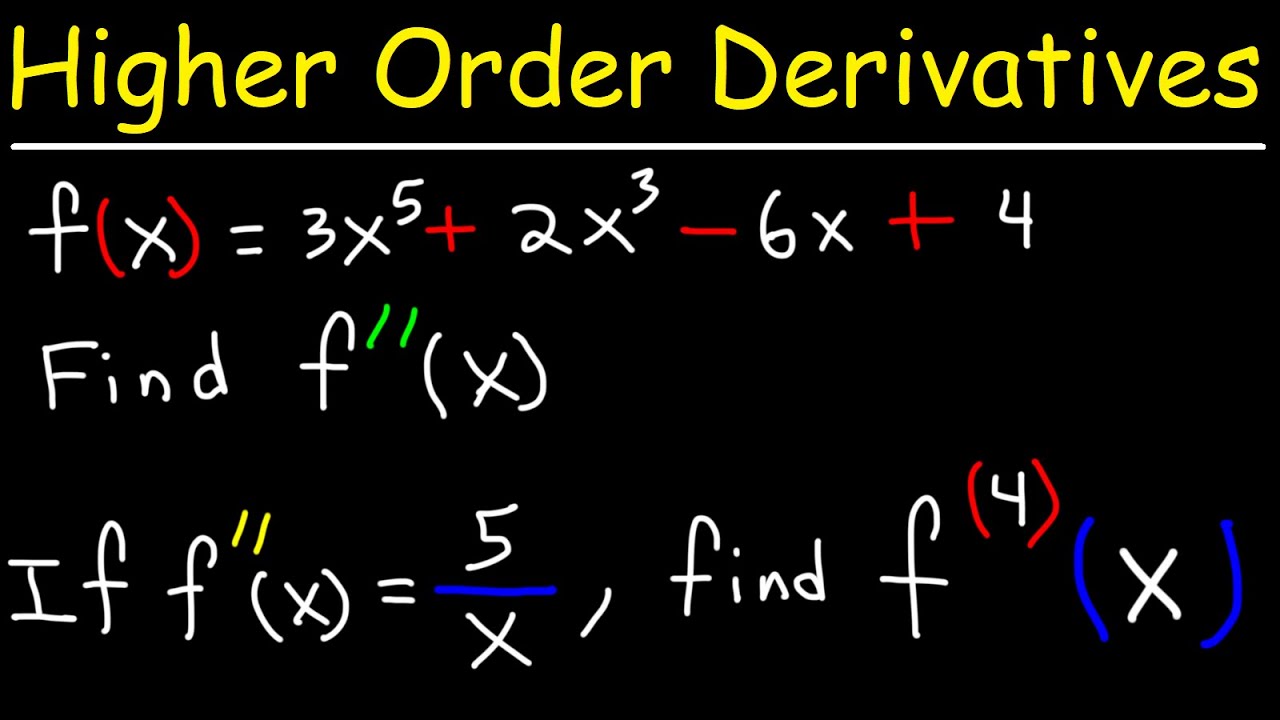
- 🔍 The script provides an example function, f(x) = x⁴ - 3x³ + 16x, and poses the task of finding its first and second derivatives.
- 📊 The process of finding derivatives involves applying the rules of differentiation to each term of the function, which is a fundamental skill in calculus.
- 📈 Understanding higher derivatives is crucial for analyzing complex functions and their behavior, which has applications in various fields of mathematics and physics.
Q & A
What is the term used to describe taking the derivative of a function?
-The term used is 'first derivative'. It refers to the process of finding the rate of change of a function with respect to its variable.
How is the first derivative of a function represented?
-The first derivative is represented as either 'dy/dx', which is the derivative of 'y' with respect to 'x', or as 'y' with a prime (y') to denote the first derivative.
What does taking the derivative of a position function yield?
-Taking the derivative of a position function yields the velocity function, which represents the rate of change of position over time.
What is the term for the derivative of a first derivative?
-The derivative of a first derivative is known as the 'second derivative'. It provides information about the rate of change of the first derivative, often representing acceleration in physical contexts.
How is the second derivative of a function represented?
-The second derivative is represented as 'd^2y/dx^2', indicating the derivative of the derivative with respect to 'x', or as 'y' with two primes (y'') to denote the second derivative.
What does the notation 'd^3y/dx^2' represent?
-'d^3y/dx^2' represents the third derivative of a function with respect to 'x'. It is a reminder to the reader that this is a third derivative, not an exponential or power of 'x'.
How can higher order derivatives be written to avoid confusion with exponents?
-Higher order derivatives can be written with parentheses around the variable and the derivative order, such as 'dy^3/dx^3', to clearly indicate that it is the third derivative and not 'y' raised to the third power.
What happens when you take an infinite number of derivatives?
-In most cases, taking an infinite number of derivatives will eventually result in a zero derivative, indicating that there is no further change in the rate of change of the function.
Given the function f(x) = x^4 - 3x^3 + 16x, what is the first derivative?
-The first derivative of f(x) = x^4 - 3x^3 + 16x is f'(x) = 4x^3 - 9x^2 + 16.
What is the second derivative of the function f(x) = x^4 - 3x^3 + 16x?
-The second derivative of f(x) = x^4 - 3x^3 + 16x is f''(x) = 12x^2 - 18x + 16.
How can the process of taking derivatives help in understanding the behavior of a function?
-The process of taking derivatives allows us to analyze the rate of change of a function, its increasing or decreasing nature, and its points of inflection. Higher derivatives can provide insights into the concavity and curvature of the function's graph, which are crucial for understanding its overall behavior.
Outlines
📚 Introduction to Higher Derivatives
This paragraph introduces the concept of higher derivatives in calculus. It explains that while the class has previously focused on first derivatives, there is the possibility of taking multiple derivatives of a function. The first derivative represents the rate of change or the slope of a function, and further differentiation can lead to higher-order derivatives, such as the second derivative which can represent acceleration in the context of velocity and position. The paragraph clarifies the notation used for derivatives, with the first derivative denoted as dy/dx or y', the second derivative as d^2y/dx^2 or y'', and so on, with each successive derivative indicated by an additional prime symbol. It also introduces alternative notations for higher derivatives, such as using parentheses to avoid confusion with exponents. The purpose of this section is to familiarize students with the terminology and notation of derivatives, and to illustrate these concepts with a few example problems.
Mindmap
Keywords
💡first derivative
💡second derivative
💡higher derivatives
💡position function
💡velocity
💡acceleration
💡notation
💡calculus
💡differentiation
💡function
💡example problem
Highlights
The class is focused on the topic of higher derivatives.
Up until now, the course has primarily discussed first derivatives.
The first derivative of a function is also known as the rate of change or the slope of the function.
Derivatives can be used to find velocity and acceleration from a position function.
The second derivative is represented as d^2y/dx^2 or f''(x).
Higher derivatives can be taken repeatedly to find further rates of change.
The third derivative is written as d^3y/dx^3 or f'''(x).
For clarity, parentheses can be used to denote higher derivatives, such as (d^3y/dx^3) for the third derivative.
An infinite number of derivatives can be taken, although eventually it may result in zero.
The notation for derivatives is a crucial aspect of understanding calculus.
The first derivative is denoted as dy/dx or f'(x), representing the function's sensitivity to changes in x.
The process of taking derivatives involves applying specific rules and formulas.
The example function f(x) = x^4 - 3x^3 + 16x is introduced to demonstrate finding derivatives.
The first derivative of the example function involves applying the power rule to each term.
The second derivative of the example function requires taking the derivative of the first derivative.
Working through problems is an effective way to illustrate and solidify understanding of derivatives.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: