BusCalc 18 Second Derivatives
TLDRThe video script delves into the concept of second derivatives, building upon the foundational knowledge of first derivatives covered throughout the semester. It explains that the second derivative is derived by taking the derivative of the first derivative, which is a measure of the rate of change of the function's rate of change. The script uses the Greek letter delta to represent small changes in both the input (x) and output (y) of a function, leading to the definition of the derivative as the limit of the ratio of these changes as they approach zero. Various notations for the second derivative are introduced, including "\frac{d^2y}{dx^2}" and "f''(x)", with the latter pronounced as 'f double prime x'. The script also illustrates the practical application of second derivatives through the example of calculating acceleration as the second derivative of distance with respect to time. The examples provided include calculating the second derivative of polynomial and exponential functions, as well as a real-world scenario involving a car's position, velocity, and acceleration during a road trip. The summary concludes with a method to find the acceleration function from a given position function by taking its second derivative, emphasizing the utility of second derivatives in understanding changes in rates of change.
Takeaways
- 📘 The second derivative is the derivative of the first derivative of a function, which represents the rate of change of the rate of change.
- 📙 The first derivative is often referred to as the instantaneous rate of change of a function with respect to its independent variable.
- 📕 Delta (Δ) represents a small change in a variable, such as Δx for a change in the input x, and Δy for the resulting change in the output y.
- 📗 The first derivative is defined as the limit of the ratio of the change in the output to the change in the input as these changes approach zero.
- 📓 The notation for the second derivative can be written as d²y/dx², f''(x), or by applying the derivative operator twice, indicating two consecutive differentiations.
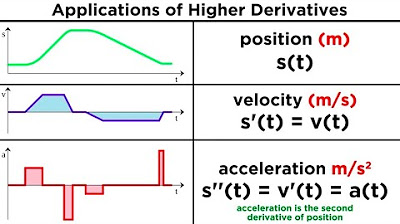
- 📒 Acceleration is a real-world example of a second derivative, as it is the rate of change of velocity (which is the first derivative of distance with respect to time).
- 📔 To find the second derivative, one must first find the first derivative and then differentiate that result once more.
- 📒 The process of finding the second derivative involves applying the derivative operator with respect to x to the ratio dy/dx.
- 📔 The second derivative can be represented in various notations, all of which mean the same thing, such as taking the derivative of the derivative of y with respect to x.
- 📘 When analyzing motion, the position function's first derivative gives velocity, and the second derivative gives acceleration.
- 📙 To calculate the acceleration at a specific time, one must evaluate the second derivative of the position function at that time.
Q & A
What is the second derivative?
-The second derivative is the derivative of the derivative of a function. It represents the rate of change of the rate of change of the function concerning the independent variable.
How is the second derivative denoted mathematically?
-The second derivative can be denoted as d^2y/dx^2, f''(x), or by applying the derivative operator twice in a row to the function y with respect to x.
What does the first derivative represent?
-The first derivative represents the instantaneous rate of change of a function, which can be thought of as the slope of the tangent line to the function's graph at a given point.
How is the change in the output of a function related to the change in the input?
-The change in the output of a function (delta y) is related to the change in the input (delta x) through the derivative, which is the ratio of delta y to delta x when these changes are infinitesimally small.
What is the physical interpretation of the second derivative in the context of motion?
-In the context of motion, the second derivative corresponds to acceleration. It is the rate of change of velocity over time, which describes how quickly the velocity of an object is changing.
How can you find the second derivative of a function?
-To find the second derivative of a function, you first find the first derivative of the function with respect to the independent variable, and then you find the derivative of that result, which is the second derivative.
What is the relationship between velocity and acceleration?
-Velocity is the rate of change of distance with respect to time, while acceleration is the rate of change of velocity with respect to time. Therefore, acceleration is the second derivative of distance with respect to time.
What is the derivative of the function y = 7x^4?
-The first derivative of y = 7x^4 is 28x^3, and the second derivative is 84x^2.
What is the second derivative of the exponential function y = e^(3x)?
-The second derivative of y = e^(3x) is 9e^(3x), as the derivative of e^(3x) with respect to x is 3e^(3x), and taking the derivative of that result gives 9e^(3x).
How do you find the acceleration function of a car given its position function?
-To find the acceleration function, you first take the first derivative of the position function with respect to time to get the velocity function, and then take the derivative of the velocity function to get the acceleration function.
What is the acceleration of a car at a specific time if its velocity function is v(t) = 10/t + 1/2t?
-To find the acceleration at a specific time, you take the derivative of the velocity function with respect to time. For v(t) = 10/t + 1/2t, the acceleration function a(t) is -10/t^2 + 1/2.
What is the acceleration of the car at t = 10, given the acceleration function a(t) = -10/t^2 + 1/2?
-The acceleration of the car at t = 10 is a(10) = -10/10^2 + 1/2, which simplifies to -1/10 or -0.1.
Outlines
📚 Introduction to Second Derivatives
This paragraph introduces the concept of second derivatives, building upon the knowledge of first derivatives covered throughout the semester. It explains that the second derivative is the derivative of the derivative, which can be represented as the ratio of a small change in the output (delta y) to a small change in the input (delta x). The limit of this ratio as delta x approaches zero is the definition of the derivative. The paragraph also covers various notations for second derivatives, such as 'd^2y/dx^2' or 'f''(x)', and touches on the practical application of second derivatives in calculating acceleration as a rate of change of velocity.
🔢 Calculating Second Derivatives
The second paragraph dives into the calculation of second derivatives for specific functions. It demonstrates the process of finding the first and second derivatives of a polynomial function (7x^4), an exponential function (e^(3x)), and a logarithmic function (ln(x)). The paragraph emphasizes the use of derivative rules, such as the power rule and the chain rule, to find these derivatives. It also highlights the notation 'f''(x)' for the second derivative and reinforces the concept that the second derivative represents the rate of change of a rate of change, exemplified by acceleration in physics.
🚗 Applying Second Derivatives to Acceleration
The final paragraph applies the concept of second derivatives to the real-world scenario of a car's motion during a road trip. It outlines how to derive the acceleration function from a given position function, emphasizing that acceleration is the second derivative of position with respect to time. The paragraph provides a step-by-step example of finding the velocity and acceleration functions for a car whose position is described by a specific function of time. It concludes with calculating the acceleration at a particular time (t=10), demonstrating the practical use of second derivatives in physics.
Mindmap
Keywords
💡Second Derivative
💡First Derivative
💡Derivative
💡Independent Variable (x)
💡Dependent Variable (y)
💡Delta (Δ)
💡Limit
💡Function
💡Acceleration
💡Velocity
💡Power Rule
Highlights
The video discusses second derivatives, which are the derivative of the derivative of a function.
The first derivative is also known as the instantaneous rate of change of a function.
The second derivative represents the rate of change of the rate of change, akin to acceleration in physics.
Notation for the second derivative includes d^2y/dx^2, f''(x), or taking the derivative with respect to x twice.
The concept of delta (Δ) is used to represent a small change in both the input (x) and output (y) of a function.
The derivative is defined as the limit of the ratio of the change in output to the change in input as the change approaches zero.
The first derivative of 7x^4 is 28x^3, and the second derivative is 84x^2.
For the function e^(3x), the first derivative is 3e^(3x), and the second derivative is 9e^(3x).
The first derivative of the natural logarithm function ln(x) is 1/x, making it the second derivative of the position function when considering motion.
Velocity is the first derivative of position with respect to time, while acceleration is the second derivative.
An example application involves calculating the acceleration function of a car during a road trip given its position function.
The acceleration function can be found by taking the second derivative of the position function with respect to time.
The value of acceleration at a specific time can be found by evaluating the acceleration function at that time.
The example provided calculates the acceleration of a car at t=10, resulting in a negative acceleration indicating deceleration.
The video uses the concept of second derivatives to explain and calculate real-world phenomena such as motion and acceleration.
Understanding second derivatives is crucial for advanced calculus and applications in physics and engineering.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: